Разложение в ряд Фурье комплексной периодической функции

Для функции с периодомL используем ортонормированный базис гармонических функций с периодом L

, ,

удовлетворяющих

.

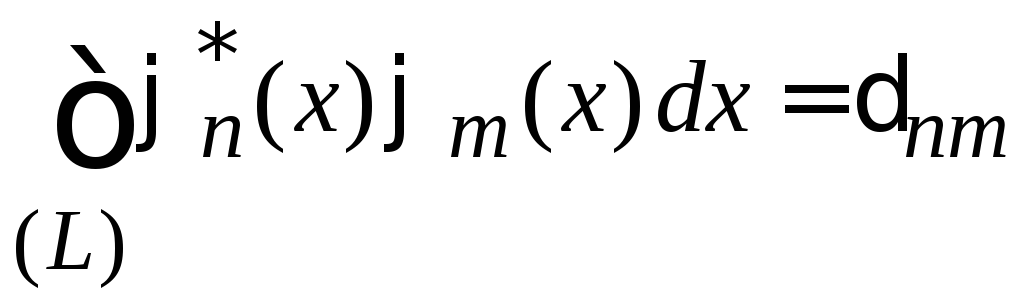Тогда функция разлагается вряд Фурье

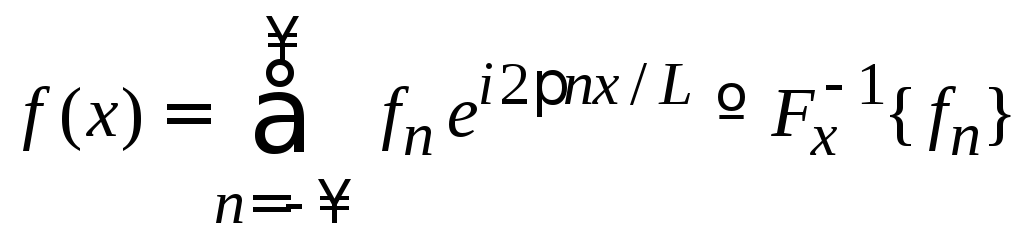. (1.48)

Ищем коэффициенты Фурье .

Умножаем (1.48) на и интегрируем по периоду

,

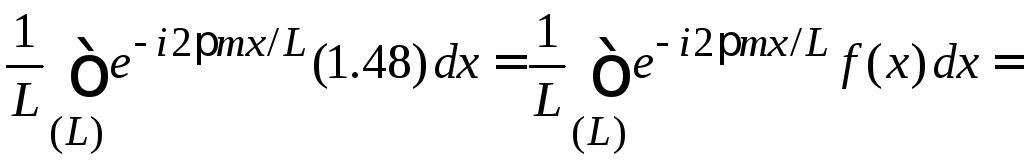
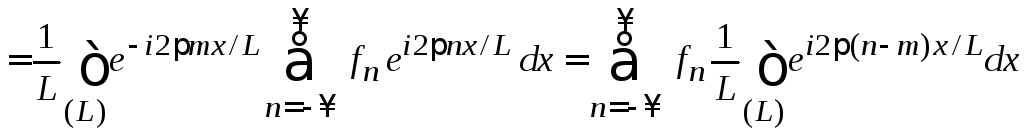где переставлено суммирование и интегрирование. С учетом (1.43)

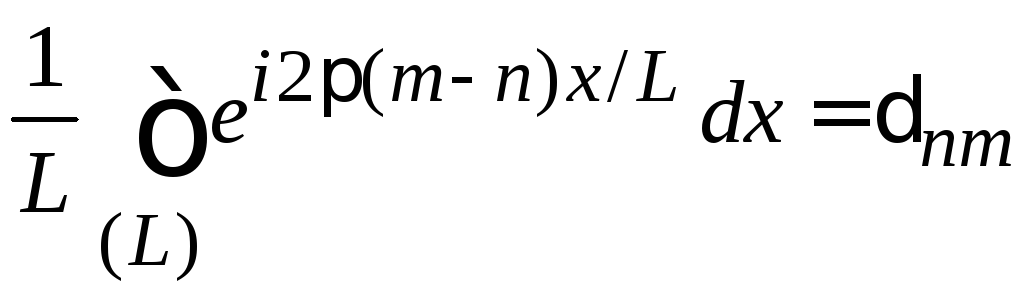
находим

.

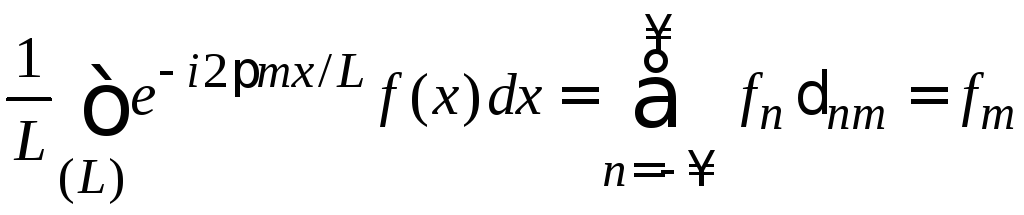Переобозначаем , и для периодической функцииполучаемкоэффициент Фурье

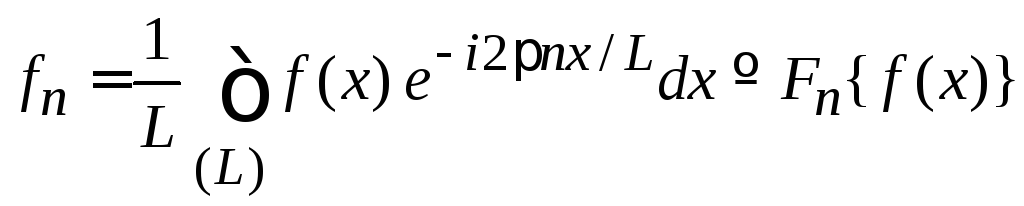. (1.49)

Фурье-образ периодической функции

Для ряда Фурье (1.48)

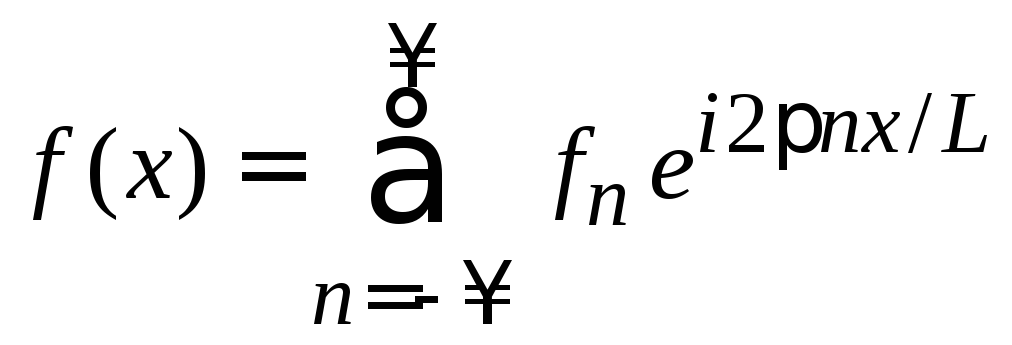
находим Фурье-образ (1.1)

.

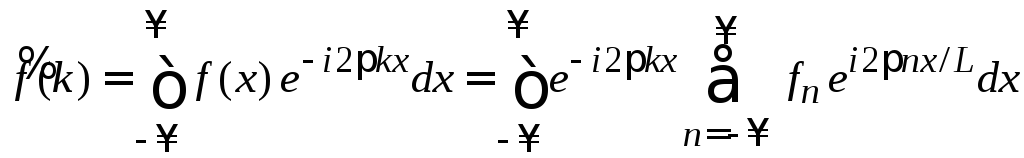Переставляем суммирование и интегрирование

.

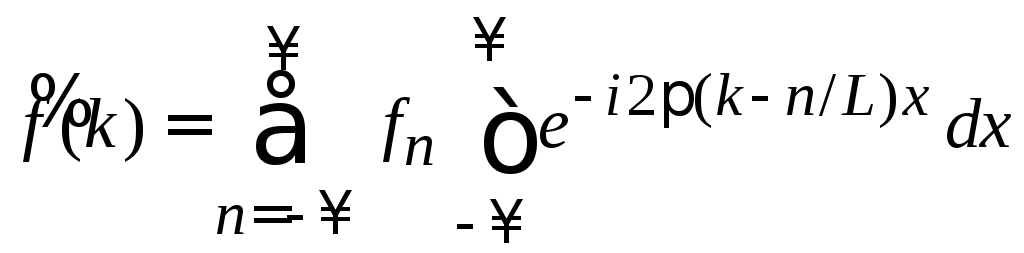Используем интегральное представление дельта-функции (2.24)

,

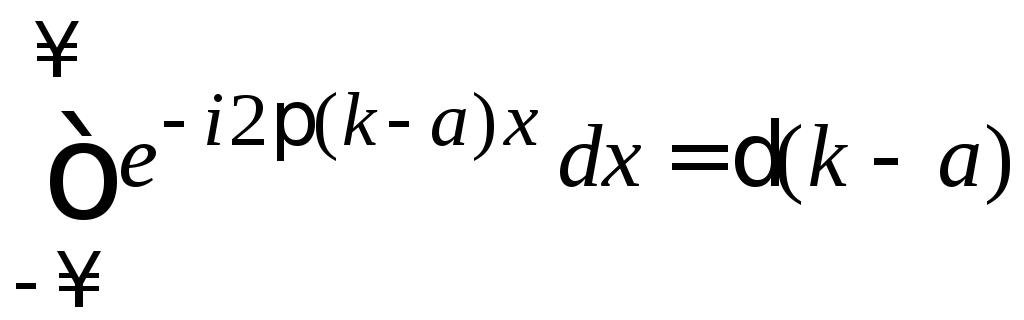получаем Фурье-образ периодической функции

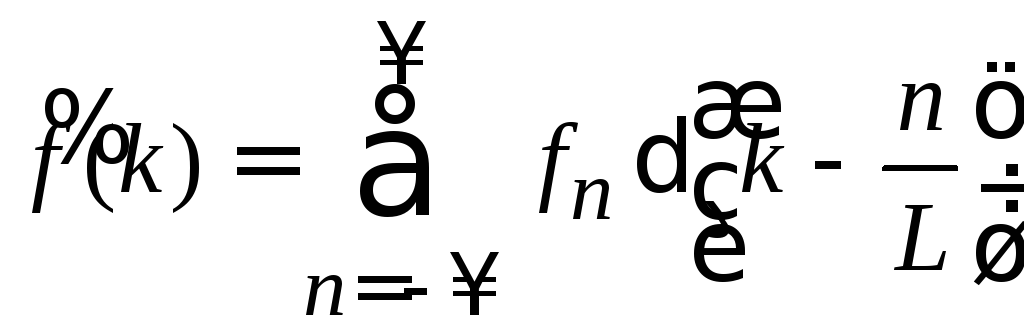. (1.47)

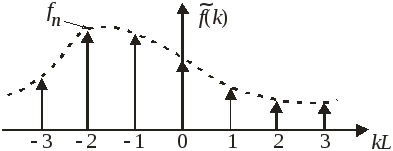
Периодическая функция с периодом L имеет спектр с периодом в виде модулированной гребенчатой функции.

Теорема о дифференцировании

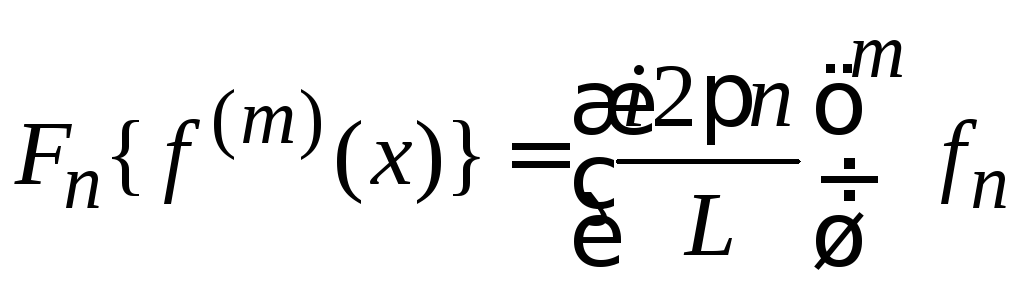. (1.50)

При m-кратном дифференцировании периодической функции ее коэффициент Фурье умножается на .

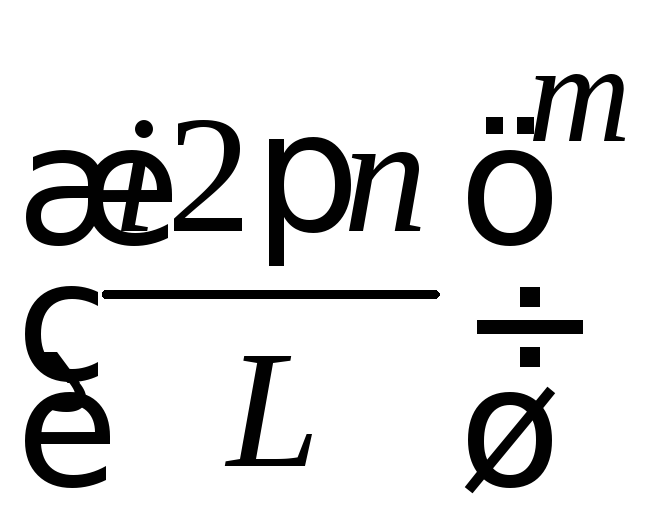Доказательство

Разложение (1.48)

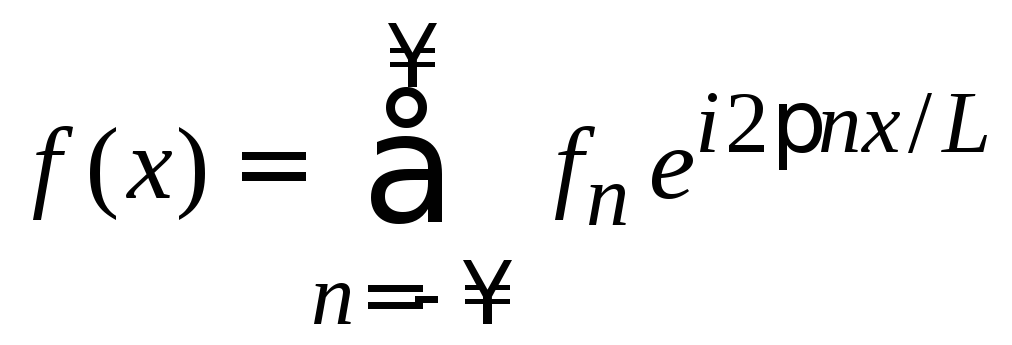
дифференцируем m раз

.

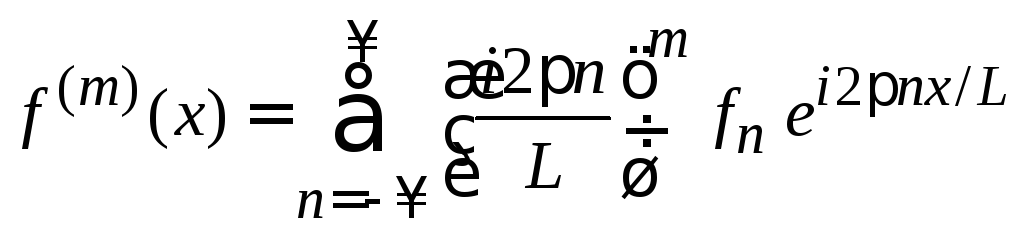Результат сравниваем с разложением (1.48)

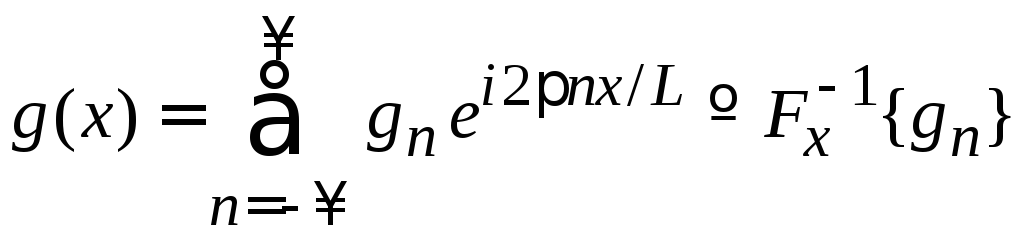
для функции , получаем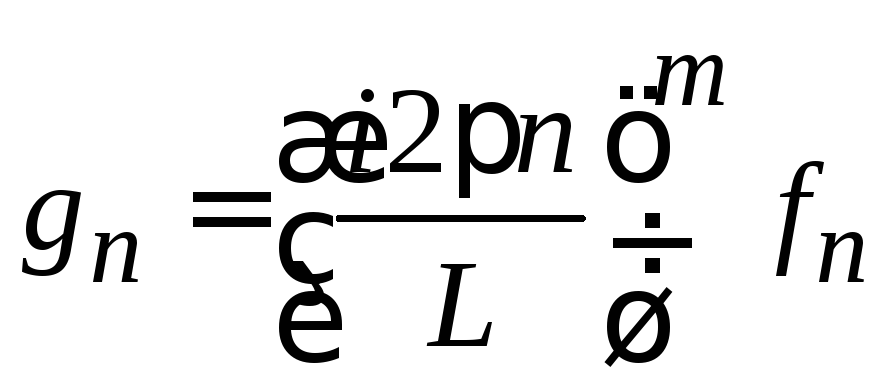, что доказывает (1.50).

Разложение в ряд Фурье вещественной периодической функции

Вещественная функция с периодом L удовлетворяет

,

.

Ищем коэффициент Фурье (1.49)

.

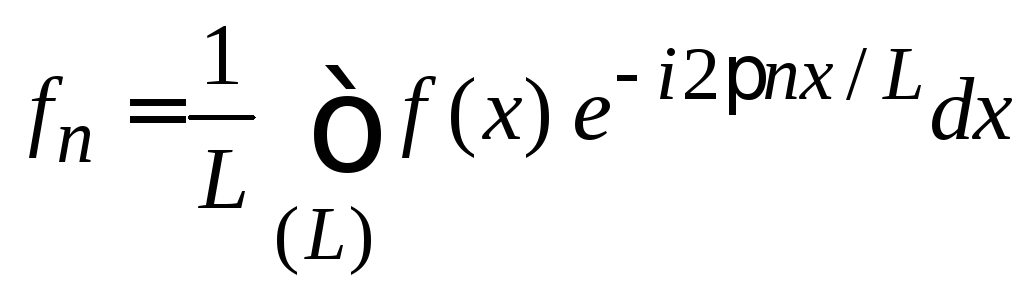Выполняем комплексное сопряжение и из условия вещественности функции получаем

,

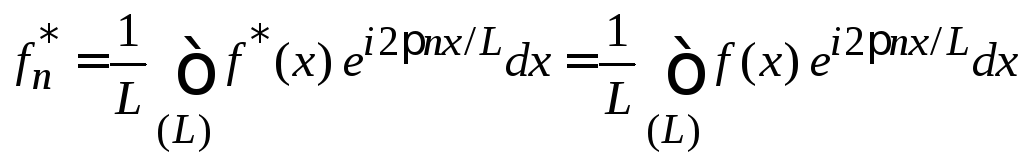Результат сравниваем с (1.49) и находим

.

Используем ряд Фурье (1.48)

.

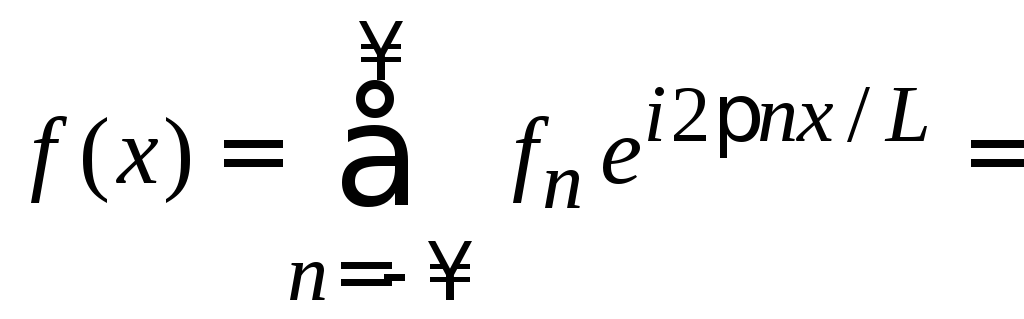
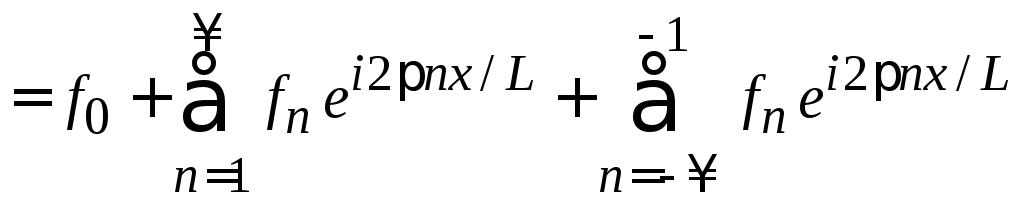С учетом получаем

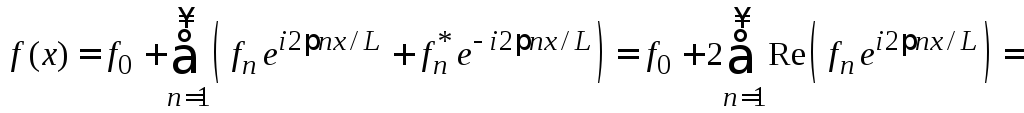
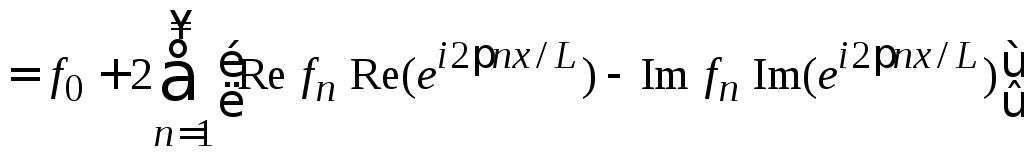, (1.53)

где учтено

,

.

Заменяем

,

где

,

.

Используем

.

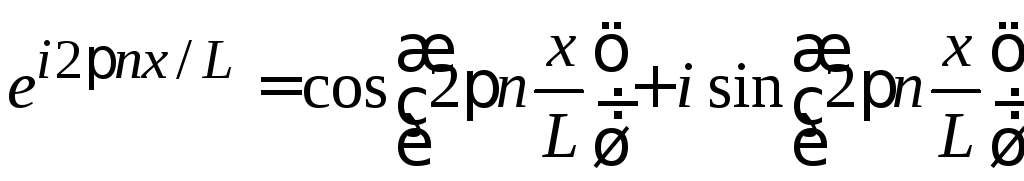Получаем разложение функции в ряд Фурье

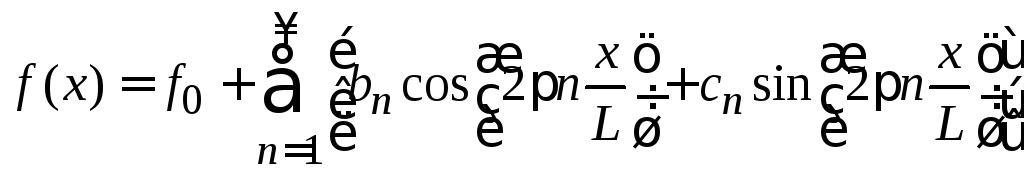. (1.54)

Из (1.49)

,

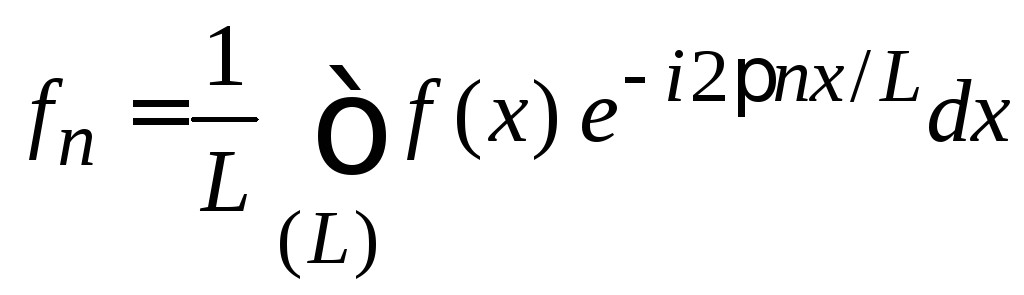находим коэффициенты Фурье

,

,

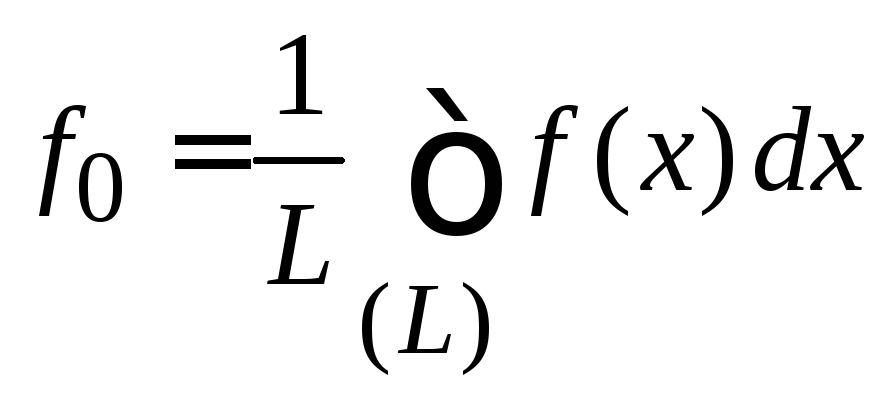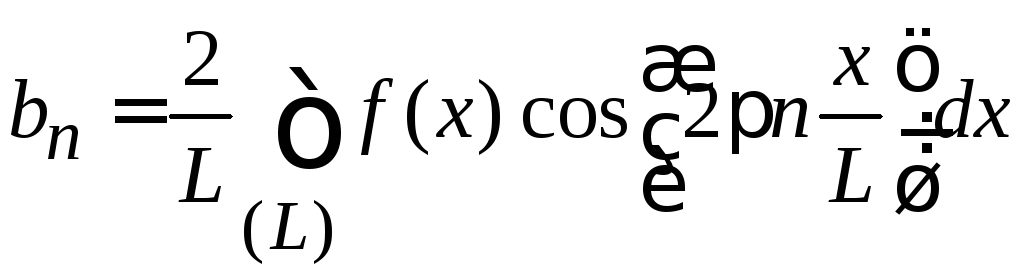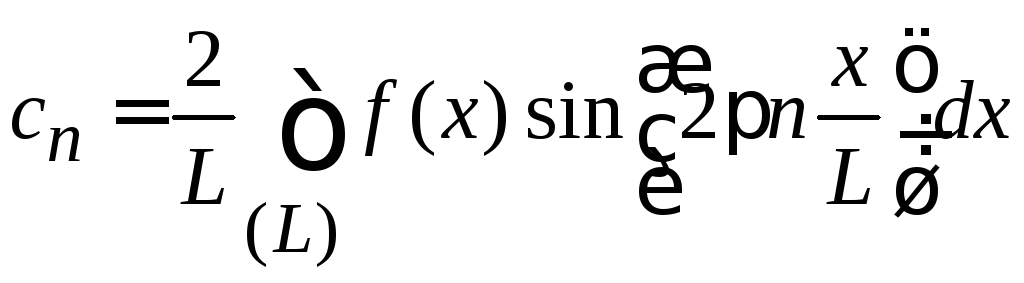. (1.54а)

36