1.2.2. Нониус

1.2.2.1. Нониус – многозначная мера длины

Представим себе две разномасштабные линейки. Сложим линейки вместе и совместим их нулевые штрихи, как показано на рис. 1.4. Пусть для определенности первая (верхняя) линейка имеет меньшие деления, длину одного деления обозначим х. Вторая (нижняя) линейка имеет большие деления, длина одного деления равнау.

Поскольку деления линеек неодинаковы, то при совпадении нулевых штрихов первые штрихи не совпадают – они находятся друг от друга на некотором расстоянии . Расстояние между вторыми штрихами равно, расстояние между третьими штрихами равнои т.д.

По мере удаления от совпадающих нулевых штрихов расстояние между штрихами с одинаковыми номерами увеличивается.

Р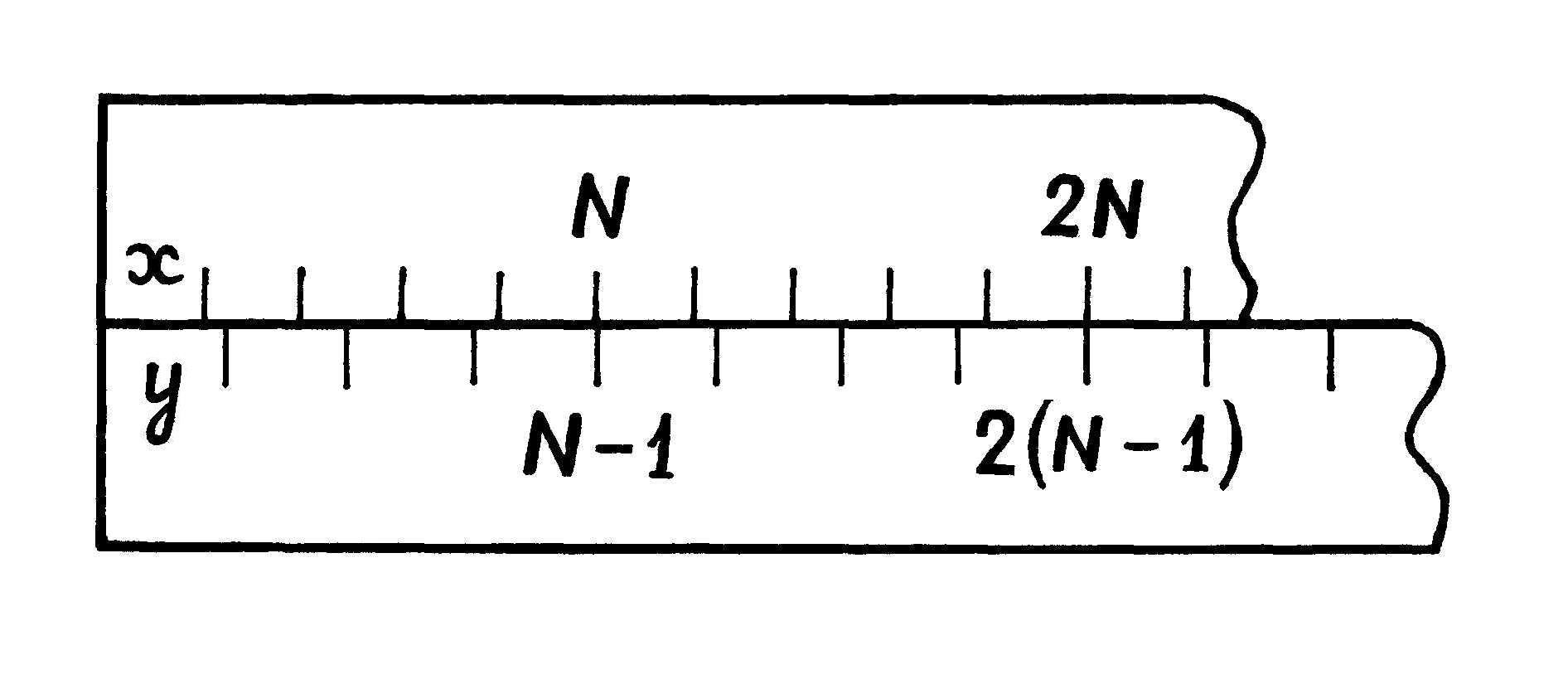асстояние между штрихами с номером (т + 1) больше расстояния между штрихами с номеромт на величинуδ.Такимобразом,две разномасштабные линейки являются многозначной мерой длины, с помощью которой можно реализовать отрезки, отличающиеся на величину .

Рис. 1.4. Две линейки, образующие нониус

Линейки образуют нониус, если существует такое целое числоN, при котором выполняется равенство

. (1.3)

Выражение (1.3) называют уравнением нониуса. Левая и правая части уравнения нониуса представляют собой расстояние между ближайшими совпадениями штрихов, выраженное через длину деления каждой из линеек.

В результате деления левой и правой части уравнения нониуса на Nуполучим, что меньшее деление составляет долю бо́льшего деления, равную

. (1.4)

Точностью нониусаназывается величина, равная разности делений линеек нониуса

. (1.5)

Точность нониуса можно выразить через длину деления каждой из линеек:

, (1.6)

. (1.7)

Из формул (1.6) и (1.7) следует, что точность нониуса составляетдолю меньшего деления либодолю бо́льшего деления линеек.Чем больше N, тем меньше эта доля.

1.2.2.2. Измерения с помощью нониуса

Сравнивать длину детали с отрезками многозначной меры, концы которых нужно искать на двух неподвижно закрепленных как указано вышелинейках, неудобно. Поступим иначе.

Начнем медленно сдвигать вправо линейку нониуса с меньшими делениями. Нулевые штрихи разойдутся. Затем совпадут первые штрихи линеек. Это произойдет при сдвиге нулевых штрихов на величину ∆l, равную точности нониуса. Вторые штрихи линеек совпадут при сдвиге нулевых штрихов на две точности нониусаи т.д. Если совпали-е штрихи, то можно утверждать, что нулевые штрихи сдвинуты на. При сдвиге ровно на одно большое делениенулевой штрих верхней линейки совпадает с первым штрихом нижней линейки и совпадают

N-ые штрихи, т.е. в этом случает = N(см. рис. 1.4).

Аналогичные наблюдения можно сделать при смещении нулевого штриха верхней линейки относительно первого штриха нижней линейки, затем относительно второго, третьего и т.д.

В любом положении линеек нониуса один из штрихов верхней линейки (из первых N) совпадает с каким-либо штрихом нижней линейки или очень близко расположен к нему. Отсчет по нониусу основан на способности глаза фиксировать это совпадение.

На практике линейку с малыми делениями делают обычно короткой, чтобы со штрихами второй линейки совпадал только один штрих этой линейки. Длинную линейку называют основной шкалойилимасштабом, короткую –дополнительной шкалой,нониусомиливерньером (по имени изобретателя – французского математика П. Вернье (1580-1637)).

Рассмотрим процесс измерений с помощью нониуса. Пусть L– длина измеряемого образца (рис. 1.5). Совместим с началом образца нулевой штрих масштаба. Пусть при этом конец образца окажется междуk-м и (k+ 1)-м штрихами масштаба. Тогда в длине образца содержитсяkцелых делений масштаба и отрезок– неизвестная пока еще доля (k+1)-го деления масштаба:

. (1.8)

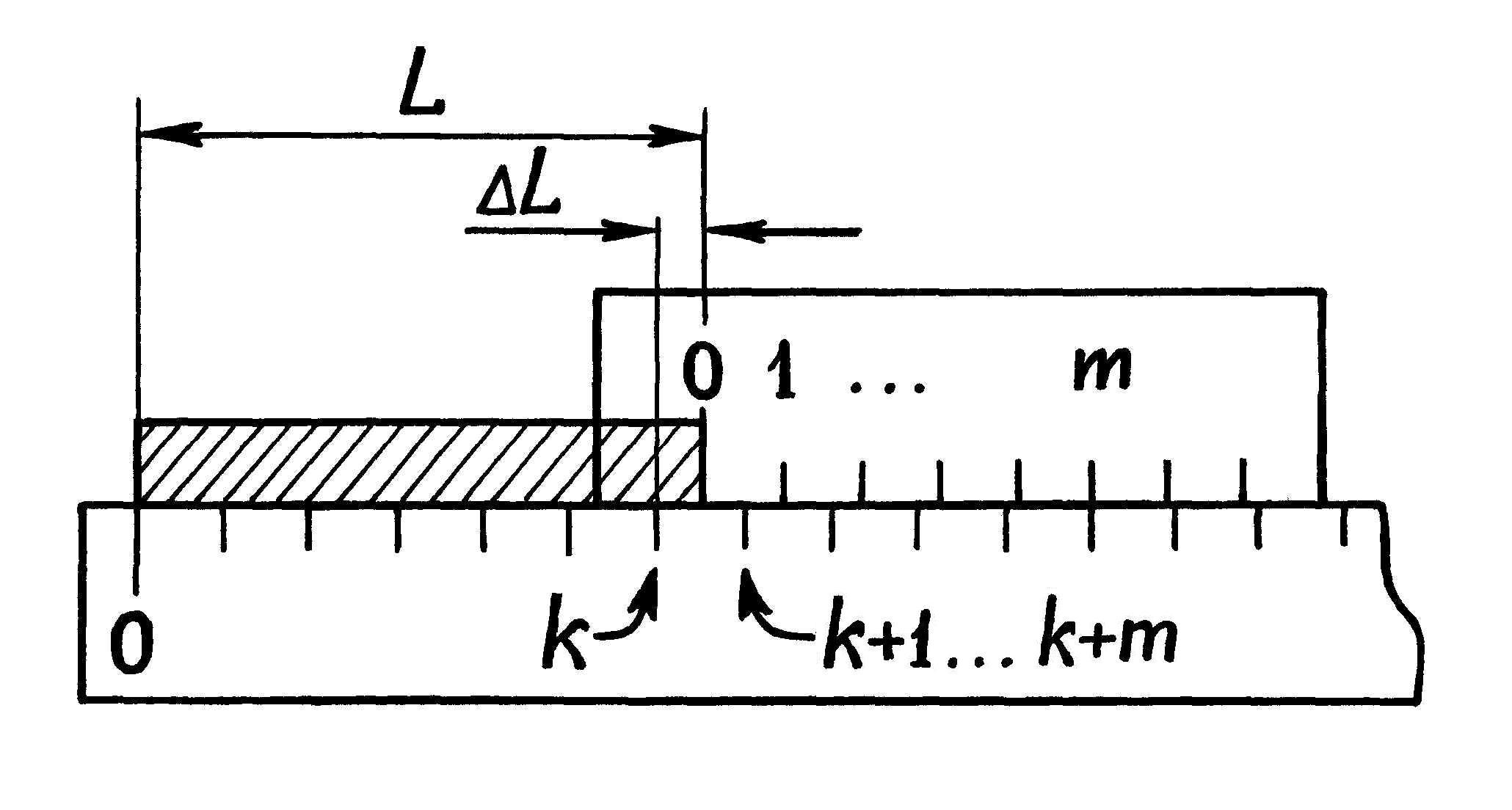
Рис. 1.5. Измерение длины детали с помощью нониуса

Для определения отрезка приложим к концу образца нониус так, чтобы нулевой штрих нониуса совпал с концом этого образца. Так как деления нониуса не равны делениям масштаба, на нем обязательно найдется такой штрихт,который будет ближе всего подходить к соответствующему (k +т)-му штриху масштаба. Как видно из рис. 1.5, отрезокравен

. (1.9)

Тогда вся длина будет равна

. (1.10)

Результат можно сформулировать следующим образом: длина образца, измеряемая с помощью нониуса, равна длине целых делений масштаба до нулевого штриха нониуса плюс отрезок, равный произведению точности нониуса на номер штриха нониуса, совпадающего с некоторым штрихом масштаба.

Погрешность, которая может возникнуть при таком методе отсчета, обусловлена неточным совпадением т-го штриха нониуса с (k +т)-м штрихом масштаба. Значение ее не будет превышать, очевидно, величину, ибо при большем несовпадении этих штрихов, один из соседних штрихов нониуса (справа или слева) имел бы несовпадение меньшеи мы произвели бы отсчет по нему.

На рис. 1.6 изображен в увеличенном виде измерительный инструмент, у которого наименьшее деление масштаба у=, наименьшее деление нониусамм, точность нониусамм,N = 10. Из рисунка видно, что расстояние между нулевыми штрихами масштаба и нониуса в случае «а» равно 0,6 мм, в случае «б» – 7,0 мм, в случае «в» – 7,4 мм.

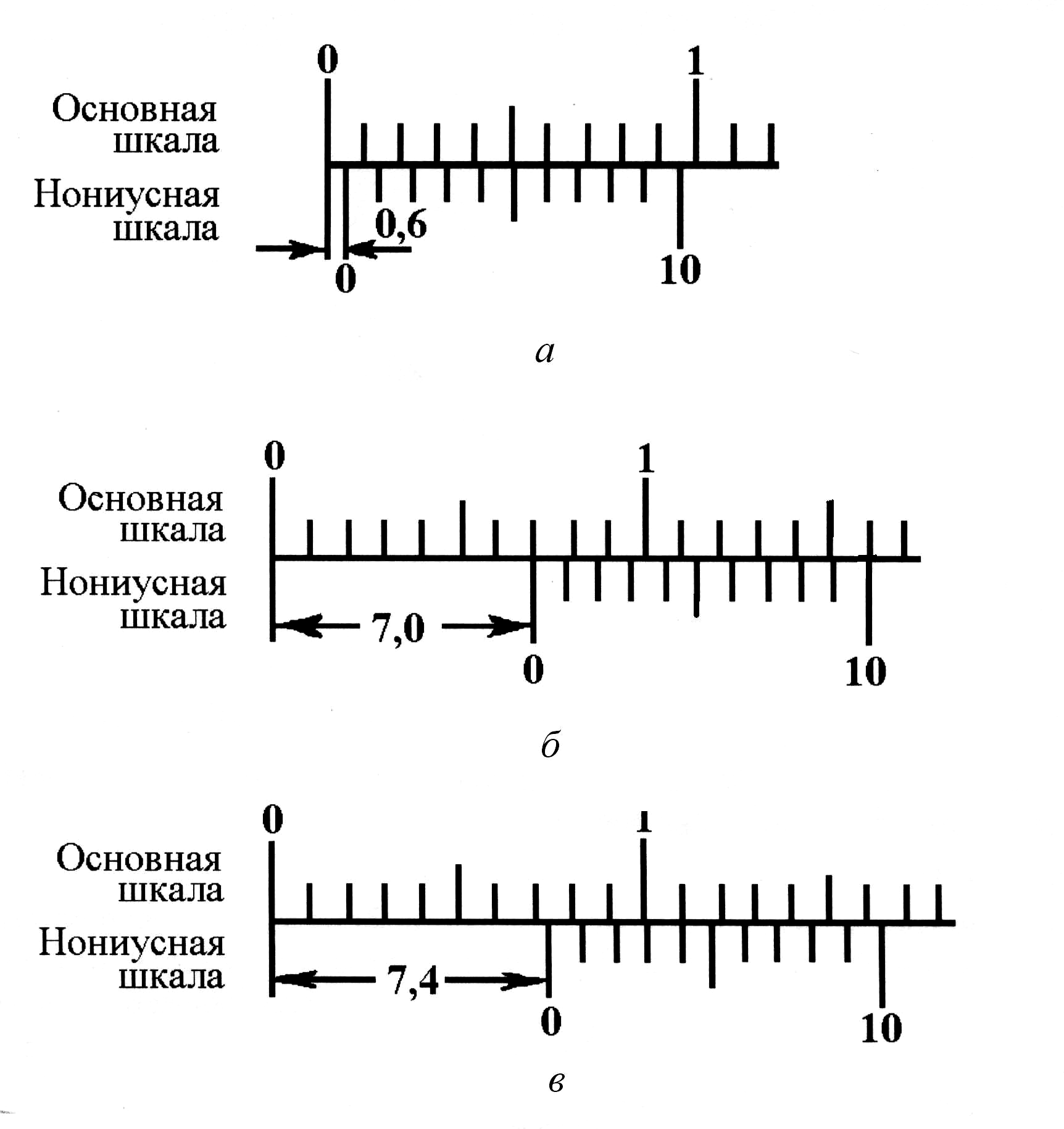
Рис. 1.6. Примеры измерений с помощью нониуса:

а  L = 0,6 мм; б  L = 7,0 мм; в  L = 7,4 мм