
УМК ТеорМех для Мех2012
.pdf
Лекция №1
Предмет теоретической механики. Модели материальных тел, изучаемые в теоретической механике. Основные понятия и законы механики. Кинематика точки. Задачи кинематики. Способы задания движения точки.
Теоретическая механика – это наука об общих законах механического движения и взаимодействия материальных тел.
Движение есть форма существования материи, наиболее простой формой движения материи является механическое движение. Механическое движение состоит в том, что с течением времени тело изменяет свое положение в пространстве по отношению к другим телам.
Для учета механического взаимодействия, возникающего между телами, в классической механике вводится понятие о силе. Кроме силы (внешний фактор), характер движения тела будет зависеть от степени инертности тела. Мерой инертности тела является его масса, зависящая от количества тела.
Таким образом, понятия, лежащие в основе классической механики, это: движущаяся материя (материальные тела); пространство и время как формы существования движущейся материи; масса, как мера инертности материальных тел; сила, как мера механического взаимодействия между телами.
Соотношения между основными понятиями механики определяется аксиомами или основными законами движения, которые были даны Ньютоном.
1-ый закон (закон инерции). Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние.
2-ой закон (основной закон динамики). Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой сила действует:
d(mv) F dt
3-ий закон (закон равенства действия и противодействия). Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.
FA FB
Теоретическая механика, как любая наука, использующая математические методы, имеет дело не с самими реальными материальными объектами, а с их моделями. Такими моделями являются материальные точки, системы материальных точек, абсолютно твёрдые тела, деформируемые сплошные среды.
Кинематика точки Основные понятия. В кинематике изучается движение тел с геометрической точки зрения
без учёта причин, вызывающих изменение этого движения, то есть сил.
Материальная точка – тело, размерами которого при изучении его движения можно пренебречь. В кинематике масса материальной точки во внимание не принимается.
Положение тела в пространстве может быть определено только относительно произвольно выбранного другого тела, называемого телом или системой отсчета. Если положение тела относительно выбранной системы отсчета со временем не изменяется, тело находится в покое относительно данной системы отсчета, если же положение тела изменяется, то это тело совершает движение относительно данной системы отсчета. Таким образом, движение и покой суть относительны, и имеют смысл только по отношению к конкретной системе отсчета.
Непрерывная линия, которую описывает движущаяся точка относительно выбранной системы отсчета, называется траекторией точки. Форма траектории зависит от системы отсчета.
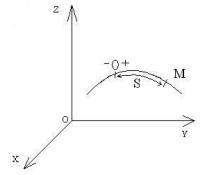
Движение тела относительно выбранной системы отсчета будет известно, если в любой произвольный момент времени можно определить его положение (относительно этой системы отсчета). Положение точки определяется соответствующими параметрами
(координатами), а движение (закон движения) – уравнениями, выражающими эти параметры как функции времени.
Установление способов, с помощью которых может быть задано движение точки, является одной из задач кинематики. Основная задача состоит в том, чтобы по уравнениям, определяющим закон движения данной точки, найти все кинематические характеристики этого движения – траекторию, скорость, ускорение и др.
Способы задания движения точки. Определить или задать движение точки, значит определить ее положение относительно выбранной системы отсчета в любой момент времени. Существует три способа задания движения точки: естественный, координатный, векторный.
1. Естественный способ требует задания траектории точки относительно выбранной системы отсчета xyz. На траектории следует задать начало и положительное направление отсчета расстояний S OM ; расстояние S (от О до М), измеренное вдоль дуги траектории и взятое с соответствующим знаком, будет однозначно определять положение точки М на траектории, а следовательно и в системе отсчета xyz. Далее необходимо указать начало отсчета времени. Движение будет определено, если для каждого момента времени t будет известна величина S, то есть, дана зависимость
S=f(t). (1)
Это равенство называется законом движения точки. Таким образом, при естественном способе определения движения точки должны быть заданы;
а) траектория точки; б) начало отсчета расстояний на траектории с указанием положительного направления
отсчета и начальный момент времени;
в) закон движения вдоль траектории в виде S=f(t).
Функция f(t) должна быть однозначной, непрерывной, дифференциальной. 2. Координатный способ. При этом способе даются:
1)какая-либо система координат, связанная с телом отсчета,
2)координаты движущейся точки как функции времени.
Так как пространство трехмерное, следовательно, требуются три числа q1,q2 ,q3 , которые называются координатами точки. Закон движения точки в общем случае задается уравнениями
q1 q1(t), q2 q2 (t), q3 q1(t) (2)
В декартовой системе координат Oxyz движение точки задается в виде
x x(t), y y(t), z z(t) (3)
Каждое из трех уравнений (3) определяет закон движения проекций точки на соответствующую ось. Уравнения (3) представляют собой, с одной стороны, закон движения точки, так как позволяют в любой момент времени определять xyz, то есть положение точки M, а с другой стороны, эти уравнения являются уравнениями траектории точки в параметрической
форме (параметр - t). |
|
|
|
|
|
||
Кроме |
декартовой |
системы |
координат |
используются |
и другие |
системы координат |
|
(сферическая, цилиндрическая). |
|
|
|
|
|||
3. Векторный способ: положение точки задается радиус-вектором |
r , проведенным из |
||||||
начала O выбранной системы отсчета. |
|
|
|
||||
Так |
как |
|
yj zk , |
то закон |
движения |
точки в |
векторной форме: |
r xi |
|||||||
|
|
y(t) j z(t)k . Траекторией точки будет годограф r . |
|
||||
r r(t) x(t)i |
|
||||||
В случае плоского движения (то есть, если траектория есть плоская кривая) закон движения выражается двумя уравнениями.
По характеру траектории движение точки может быть прямолинейным и криволинейным
(эти свойства зависят от выбора системы отсчета).
Лекция №2
Скорость и ускорение. Разложение скорости и ускорения на радиальную и трансверсальную составляющие. Разложение ускорения по осям естественного трехгранника.
Вектор скорости точки Скорость точки характеризует быстроту и направление движения точки и равна
производной радиуса-вектора точки по времени:
v dr r dt
Вектор скорости направлен по касательной к траектории.
Вектор ускорения точки Ускорение точки – векторная величина, характеризующая изменение с течением времени
модуля и направления скорости точки. Ускорение точки равно первой производной по времени от вектора скорости или второй производной по времени от радиуса-вектора скорости:
|
dv |
|
d2r |
|
w |
|
|
|
. |
dt |
dt2 |
|||
Вектор ускорения всегда направлен в сторону вогнутости траектории.
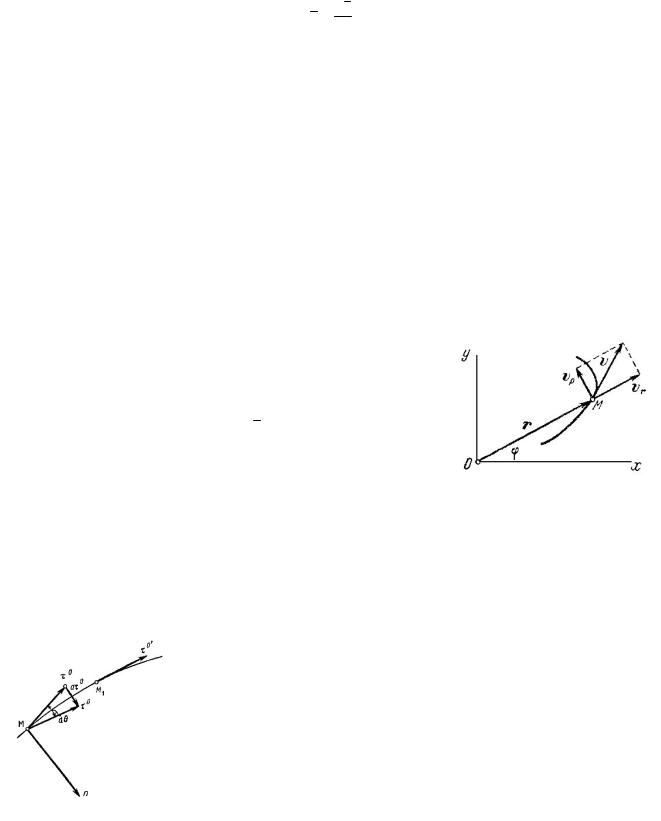
Разложение скорости на радиальную и трансверсальную составляющие
Представим радиус-вектор в виде: r rr0 , где r0 единичный вектор направления
Радиус-вектор r меняется и по длине и по направлению, следовательно, r и r0 от времени t. Продифференцируем радиус-вектор по времени:
|
|
dr |
|
dr 0 |
|
dr0 |
||
v |
|
|
|
|
r |
|
|
r. |
dt |
|
|
||||||
|
|
|
dt |
|
dt |
|||
Первое слагаемое характеризует изменение r по модулю. Направление второго слагаемого перпендикулярно r0 , так как
дифференциал |
единичного |
|
вектора |
|
|
перпендикулярен |
||||||||||
направлению |
самого вектора, |
а |
|
dr |
0 |
|
|
d |
. |
Таким |
образом, |
|||||
|
|
|||||||||||||||
|
dt |
|
dt |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
второе слагаемое характеризует изменение r |
по направлению. |
|||||||||||||||
То есть, |
|
|
|
|
|
|
|
dr |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|||||
|
v vr |
vp |
|
|
r |
|
r |
|
p |
|
, |
|||||
|
|
dt |
|
dt |
|
|||||||||||
r.
-функции
где первое слагаемое – радиальная составляющая скорости, а второе – трансверсальная.
Разложение ускорения на радиальную и трансверсальную составляющие
|
|
dr |
|
0 |
|
|
d |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как v |
|
|
r |
|
r |
|
|
p |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
dt |
|
|
|
|
dt |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||
|
|
d |
2 |
|
|
|
|
|
|
|
|
|
dr d |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
dv |
|
|
r |
0 |
|
dr dr |
|
0 |
|
d |
|
0 |
|
d dp |
|
|
|
||||||||||||||||||
w |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
p |
|
r |
|
|
|
p |
|
r |
|
|
|
. |
|
|||||||
dt |
|
dt2 |
|
dt |
|
dt |
dt |
dt |
|
dt2 |
|
dt |
dt |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp0 |
|
|
|
|
|
|
0 |
|
||
Найдем |
модуль |
|
и |
|
направление |
|
вектора |
|
|
|
. |
|
d p |
p |
|
|
- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
dt
дифференциал единичного вектора перпендикулярен направлению
самого вектора и направлен противоположно r0 (направление d p0 получается поворотом p0
на 90° в сторону положительного отсчета угла). Кроме того, dp0 d , следовательно dt dt
|
|
|
|
|
|
|
|
|
|
d 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
dp0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(*) |
|||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Подставим в выражение w: |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2r |
|
|
d |
|
2 0 |
|
|
|
|
|
d2 |
|
dr d 0 |
|
|||||||||||||||||
w |
|
|
|
|
r |
|
|
|
|
r |
r |
|
|
|
|
|
2 |
|
|
|
p |
. |
||||||||||
dt |
2 |
|
|
|
|
|
|
dt |
2 |
|
dt |
|
dt |
|||||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
d2r |
|
|
d |
2 |
0 |
|
|
|
|
|
|
|
|||||||||||||
Радиальная составляющая |
|
|
wr |
|
|
|
|
|
|
r |
|
|
|
|
|
r |
|
|
|
направлена по радиус-вектору. |
||||||||||||
|
|
|
dt2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Трансверсальная составляющая |
|
|
|
|
|
d2 |
|
|
dr d |
0 |
перпендикулярна к радиус-вектору. |
|||||||||||||||||||||
wp |
|
r |
|
|
|
|
|
|
2 |
|
|
|
|
p |
|
|
||||||||||||||||
|
dt |
2 |
|
|
dt |
|
dt |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
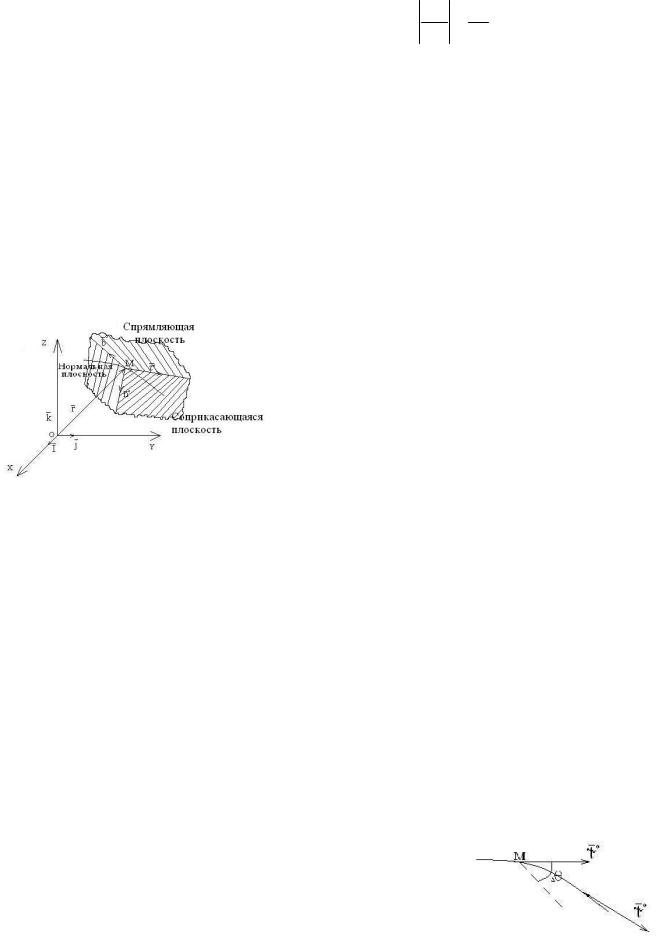
Естественный трехгранник
1) Проведем касательную в точке М, положительное направление определим единичным вектором 0 (в сторону возрастания криволинейной координаты S). Соприкасающаяся плоскость –
предельное положение плоскости, проходящей через какие-нибудь три точки кривой, когда эти точки стремятся к М, или предельное положение плоскости, проходящей через касательную M и точку M', когда M' M .
2)Проведем через точку М плоскость,
перпендикулярную к касательной 0 . Эта плоскость называется нормальной плоскостью траектории в точке М. Все прямые, лежащие в этой плоскости называются нормальными, а линия пересечения нормальной плоскости с соприкасающейся плоскостью, называется главной нормалью. Положительное направление главной нормали – в сторону вогнутости траектории. Единичный вектор - n0 .
3) Прямая, перпендикулярная к касательной и к главной нормали, называется бинормалью.
Единичный вектор - b0 . Положительное направление выбирают так, |
чтобы |
|
|
||
0 , b0 , |
n0 |
||||
образовывали правую тройку. |
|
|
|
|
|
|
|
|
|
|
|
Эта система осей называется естественными осями. Плоскость, проходящая через ( 0 , |
|||||
|
|
|
0 ) – |
спрямляющей. |
|
n0 ) называется соприкасающейся, |
(n0 , b0 |
) – нормальной, (b0 , |
|||
Прямоугольный триэдр с вершинами в точке М является естественным трехгранником, он
движется по траектории вместе с точкой М.
|
|
|
|
|
|
Кривизна кривой |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0', а длину дуги |
|
Если обозначить через - угол смежности между касательной |
и |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
ММ' S , то |
|
k |
- средняя кривизна кривой на отрезке |
|
|
|
||||
S |
|
|
|
|||||||
|
ср |
|
|
|
d |
|
|
|
|
|
ММ'. В пределе при S 0: lim |
|
k - кривизна кривой |
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
S 0 |
S dS |
|
|
|
|||
(не постоянна, меняется).
Величина |
1 |
|
dS |
называется радиусом кривизны. |
|
k |
d |
||||
|
|
|
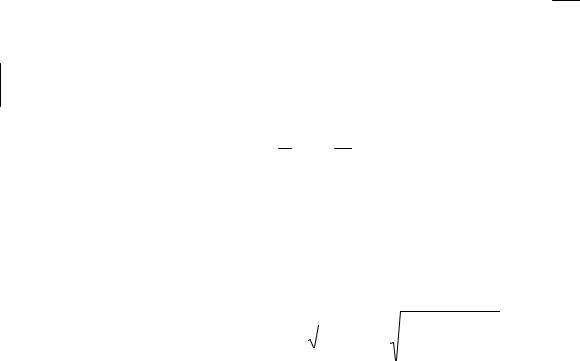
Разложение ускорения по осям естественного трехгранника
|
v |
|
|
|
|
|
|
|
|
|
||
v |
|
0 v |
0 |
|
|
|
|
|||||
|
|
|
|
|
dv 0 |
|
0 |
|
||||
|
|
dv |
|
|
d |
|
||||||
w |
|
|
|
|
|
|
|
|
|
|
v |
|
dt |
|
|
dt |
|
||||||||
|
|
|
dt |
|
|
|
|
|||||
Первое слагаемое направлено по касательной. Рассмотрим второе слагаемое d 0 v . Вектор dt
d 0 направлен по нормали к n0 . По модулю он равен
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
d |
|
|
d |
|
(lim |
|
|
|
|
|
|
lim |
|
lim |
|||||||
|
|
|
|
|
|
|
|||||||||||||||
dt |
|
dt |
|
|
|
|
t |
|
|
|
|||||||||||
|
|
|
t 0 |
|
|
|
|
t 0 t t 0 |
|||||||||||||
|
|
|
d |
|
|
d dS |
|
|
1 |
|
|
|
|
|
|
|
0 |
||||
Но |
|
|
|
|
v , тогда |
d |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
dt |
dS dt |
|
|
dt |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv 0 |
|
|
v2 0 |
|
||
Окончательно, |
|
w |
|
|
|
|
|
n |
. |
||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
||
sin |
|
|
|
|
|
||
|
|
|
|
|
|||
2 |
|
lim |
). |
||||
|
|
|
|||||
|
|
|
|
t 0 t |
|||
2
v v n0v v2 n0 .
w |
|
dv |
- тангенциальная или касательная составляющая, w |
v2 |
|
|
|
|
- нормальная |
||
dt |
|
||||
|
|
n |
|
||
составляющая.
Так как wb 0, то w в соприкасающейся плоскости.
|
|
|
|
|
|
2 |
|
|
v |
2 |
2 |
||
|
2 |
2 |
|
|
|
|
|||||||
|
|
|
dv |
|
|
|
|
||||||
Ускорение по абсолютной величине: w |
w |
wn |
|
|
|
|
|
|
|
||||
|
|
|
. |
||||||||||
|
|
|
|
|
dt |
|
|
|
|||||
Угол - угол между wи главной нормалью: tg |
w |
. Если угол между w и v острый, то |
|||||||||||
wn |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
движение ускоренное, если тупой – движение замедленное.
Лекция №3
Кинематика системы и абсолютно твердого тела. Механическая система. Число степеней свободы системы и абсолютно твердого тела. Основные движения абсолютно твердого тела. Поступательное движение абсолютно твердого тела. Скорость и ускорение при поступательном движении.
Механической системой называется множество материальных точек, в котором движение каждой точки зависит от положения и движения остальных точек системы.
Положение системы из n точек известно, если известны координаты всех точек системы, то есть: x1, y1, z1, x2 , y2, z2 ,..., xn , yn , zn .
Зависимость между движениями точек возникает: 1) вследствие сил взаимодействия между ними; 2) вследствие наличия связей.
Связями называют условия, которые налагают ограничения на движение точек системы.
Аналитически связи выражаются уравнениями, которым в любой момент времени должны удовлетворять или координаты точек системы (геометрическая связь), или координаты и скорости точек системы (кинематическая связь):
f x1, y1, z1, x2, y2, z2,..., xn , yn, zn; t 0- геометрическая связь
x1, y1, z1, x2, y2, z2,..., xn , yn , zn; x1, y1, z1, x2, y2, z2,..., xn , yn , zn; t 0 - кинематическая связь.

Пусть на систему наложено k геометрических связей: f x1, y1,...., zn; t 0, ( 1, k)
Тогда из 3n координат независимых будет (3n-k) координат; то есть, если задать 3n-k какихлибо координат, остальные определятся из уравнений связей. Эти независимые координаты называют координатами системы. В случае только геометрических связей число координат системы называется числом степеней свободы системы.
Абсолютно твердым телом или неизменяемой системой называется такая механическая система, в которой расстояние между любыми двумя точками неизменно.
Основные движения твердого тела
Различают 5 видов движения твердого тела:
1)поступательное движение;
2)вращательное движение;
3)плоскопараллельное или плоское движение;
4)сферическое движение;
5)общий случай движения твердого тела.
Поступательное и вращательное движения являются простейшими, основными движениями твердого тела.
Поступательное движение твердого тела
Поступательным движением называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.
Теорема. Все точки твердого тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Таким образом, изучение поступательного движения твердого тела можно свести к
изучению движения отдельной точки этого тела, то есть к задаче кинематики точки.
Вектора v и w - свободные, то есть их можно приложить к любой точке тела. Они называются скоростью и ускорением поступательного движения твердого тела.
При любом другом движении твердого тела точки тела движутся с различными скоростями и ускорениями.
Уравнения поступательного движения твердого тела – уравнения движения любой его точки (обычно центра масс).
xc f1(t) yc f2 (t)
zc f3(t)
Точки твердого тела, движущегося поступательно, могут описывать любую траекторию, в том числе и прямую.
Если скорость постоянна, то все точки системы движутся прямолинейно и равномерно. То есть система совершает инерциальное движение.
Если скорости всех точек неизменяемой системы равны между собой только для какоголибо момента t, то мы говорим, что неизменяемая система в данный момент времени имеет
мгновенную поступательную скорость.
Лекция №4
Вращательное движение абсолютно твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение твердого тела. Скорость и ускорение точек твердого тела.
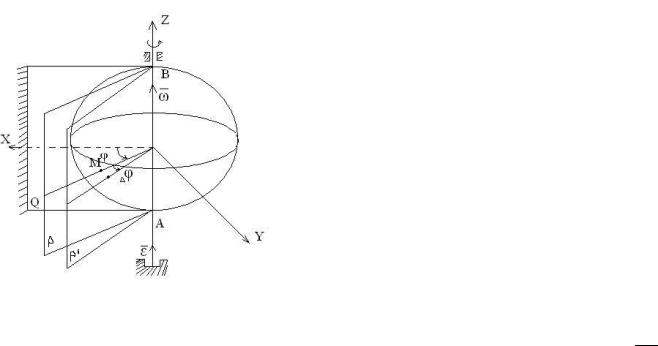
Если твердое тело движется так, что две его точки A и B остаются неподвижными, то движение тела называется вращательным, а прямая AB - осью вращения. При вращательном движении траектория всех точек – окружности, плоскости которых перпендикулярны оси
вращения, а центры лежат на этой оси.
Пусть ось вращения AB совпадает с осью z. Чтобы определить положение вращающегося тела, проведем через ось z две плоскости: Q - неподвижную и P - неизменно связанную с телом, неподвижную. Двугранный угол между неподвижной Q и подвижной P, называется углом поворота тела. 0, если с положительного конца оси z угол виден отложенным от неподвижной плоскости противоположно часовой стрелке.
Заданием величины и знака вполне определяется положение плоскости P, а следовательно, и положение тела. То есть, можно рассматривать как угловую координату тела. Угол поворота изменяется с течением времени, следовательно, является функцией времени:
(t) - закон вращательного движения.
Итак, при вращательном движении тело имеет одну степень свободы.
Если за промежуток времени t угол получает приращение , то величина t
называется средней угловой скоростью тела за данный промежуток времени. Переходя к пределу, получим:
|
|
|
|
d |
|
|
- угловая скорость вращения твердого тела. |
||||||
lim |
|
|
|
|
|
||||||||
t |
dt |
||||||||||||
t 0 |
|
|
|
|
|
|
|
|
|||||
В общем случае |
угловая скорость с течением времени изменяется, то есть (t). Если |
||||||||||||
приращение за t |
равно |
, то величина |
|
|
является средним угловым ускорением |
||||||||
|
|||||||||||||
|
t |
||||||||||||
тела за данный промежуток времени. В пределе получим: |
|||||||||||||
|
|
lim |
|
|
d |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
t |
dt |
- угловое ускорение тела. |
|||||||||
|
|
|
t 0 |
|
|
|
|
|
|||||
Угловая скорость в данный момент характеризуется вектором , направленным по оси
вращения. Длина вектора соответствует значению модуля |
|
, а направление будет таким, |
|
чтобы вращение с конца вектора было противоположным часовой стрелке.
Угловое ускорение – также вектор, , направленный вдоль оси вращения. Если направление и совпадают – движение ускоренное, если противоположно , то движение замедленное.
Если во все время движения const , то вращение называется равномерным. Закон такого движения: 0 t .
Если во все время движения const , то такое движение называется равнопеременным.
Закон этого вращения: 0 0 t |
t |
2 |
. |
|
|
|
|
||
2 |
|
|
t |
|
При этом угловая скорость изменяется по закону: 0 |
||||
Угол поворота часто выражают |
числом оборотов |
N. Тогда угол в радианах, |
||
соответствующий N оборотам, определяется как 2 N . |
|
|||
Момент вектора. Для неподвижного или скользящего вектора можно ввести понятие момента относительно центра и относительно оси.
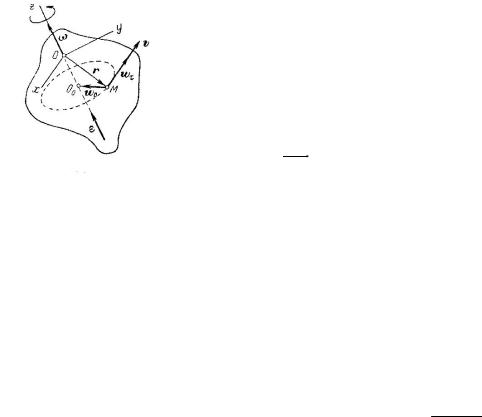
Пусть вектор a приложен в точке M . Положение точки M относительно Oxyz определяется
радиусом-вектором r .
r xi yj zk .
Моментом вектора a относительно центра O называется векторное произведение
r a : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
momOa r a |
|
x |
y |
|
z |
, |
|
momOa |
|
r a sin(r ,a) |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
ax ay az |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Направление векторного произведения определяется по «правилу буравчика». |
|
|
|||||||||||||||||||||||||||||
Как и любое |
векторное |
произведение, момент |
momOa |
по модулю |
равен |
площади |
|||||||||||||||||||||||||
параллелограмма, натянутого на вектора r |
и a, то есть равно ah rasin(r |
|
|
|
|
||||||||||||||||||||||||||
,a). |
|
|
|||||||||||||||||||||||||||||
Моменты относительно осей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y |
|
z |
|
|
|
|
|
|
|
|
|
|
z |
x |
|
|
|
|
|
|
|
|
|
x |
y |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Mx |
momxa |
ay |
az |
, My |
momya |
az |
ax |
|
, |
Mz |
momza |
|
ax |
ay |
|
|
|||||||||||||||
|
|
|
Скорости и ускорения точек вращающегося твердого тела |
||||||||||||||||||||||||||||
|
Любая точка М твердого тела совершает круговое движение, то |
||||||||||||||||||||||||||||||
|
есть vM O0M . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Тогда, |
|
v |
|
|
|
|
|
, |
так как O0M - плечо вектора относительно |
|||||||||||||||||||||
|
|
|
momM |
|
|||||||||||||||||||||||||||
|
точки М. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
momM |
|
|||
|
По |
определению |
|
момента: |
|
v совпадает |
|
с |
и по |
||||||||||||||||||||||
|
направлению, то есть vM momM . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Если О произвольная точка оси, в которой приложен скользящий |
||||||||||||||||||||||||||||||
|
вектор , |
и r OM , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
vM momM |
MO |
OM r |
r . |
|
|||||||||||||||||||||
Таким образом, для любой точки вращающегося твердого тела скорость определяется
формулой Эйлера:
v r
Возьмем произвольную точку О на оси вращения за начало системы координат Oxyz , Oz - вдоль оси вращения, тогда:
|
|
|
|
|
|
vx y |
|
|
|
i |
j |
k |
|
0 |
0 |
|
|
|||
v |
r |
vy x |
||||
|
|
|
x |
y |
z |
|
|
|
|
vz 0 |
|||
Ускорение любой точки М вращающегося тела также находится по формулам кругового движения:
w O0M , wn O0M 2, w 
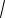 2 4 .
2 4 .
wn всегда направлен по радиусу окружности и его называют центростремительным
ускорением, w - вращательным ускорением.
Если скорости точек тела, лежащих на оси АВ равны нулю во все время движения, то эта ось называется перманентной или постоянной осью вращения.
Если же скорости точек тела, лежащих на некоторой оси, равны нулю только в данный момент времени, то эта ось называется мгновенной осью вращения. Скорости всех точек в этом случае также определяются формулой Эйлера, где , направленная вдоль мгновенной оси вращения, называется мгновенной угловой скоростью тела. В отличие от перманентной,
мгновенная ось непрерывно изменяет направление как в самом теле, так и по отношению к
|
|
||
основной системе отсчета. Тогда |
|
d |
не будет совпадать по направлению с угловой |
|
|||
скоростью вращения . |
|
dt |
|
|
|
|
|
Лекция №5
Плоскопараллельное движение абсолютно твердого тела. Основные понятия. Скорости точек плоской фигуры. Мгновенный центр скоростей. Геометрическое рассмотрение плоскопараллельного движения. Центроиды.
Плоскопараллельное движение абсолютно твердого тела Плоским или плоскопараллельным движением твердого тела называется такое
движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Плоская фигура, образованная сечением тела этой неподвижной плоскостью Q, во все время движения остается в этой плоскости.
Рассмотрим две точки тела, расположенные на одном перпендикуляре к неподвижной плоскости Q. Точка M1 движется в плоскости Q1||Q, точка M2 - в плоскости Q2||Q. При движении отрезок M1M2 остается перпендикулярным к Q, следовательно, параллельным самому себе. То есть все точки перпендикуляра M1M2 описывают тождественные и параллельные между собой траектории и имеют геометрически равные скорости и ускорения, то есть траектории А1В1, А2В2, АВ тождественны и параллельны, в данный момент времени
равны их скорости v1 v2 |
v и ускорения w1 w2 w. |
Таким образом, движение каждой точки плоской фигуры в |
|
неподвижной плоскости |
определяет собой движение всех |
точек твердого тела, расположенных на перпендикуляре к плоскости Q, это позволяет свести изучение плоского движения твердого тела к изучению движения плоской фигуры в ее плоскости.
Так как положение плоской фигуры на плоскости определяется положением двух точек или отрезка, содержащего две точки, то движение плоской фигуры можно изучать как движение прямолинейного отрезка в этой плоскости.
Основными видами плоской фигуры в ее плоскости являются поступательное и вращательное.
Поступательным движением плоской фигуры будет движение, при котором любая прямая в плоскости движущейся фигуры перемещается параллельно самой себе.
Вращательным движением фигуры в ее плоскости будет движение, при котором одна точка фигуры, называемая центром вращения остается неподвижной. Здесь все точки фигуры движутся по окружностям, имеющим центры в центре вращения.
|
|
|
|
|
|
, tg |
w |
|
|
Причем, v |
|
AB , |
w |
OM |
2 4 |
|
|||
|
w |
2 |
|||||||
|
B |
|
M |
|
|
|
|
||
|
|
|
|
|
|
|
n |
|
|
(Ускорение отклонено от радиуса вращения на угол , который одинаков для всех точек)
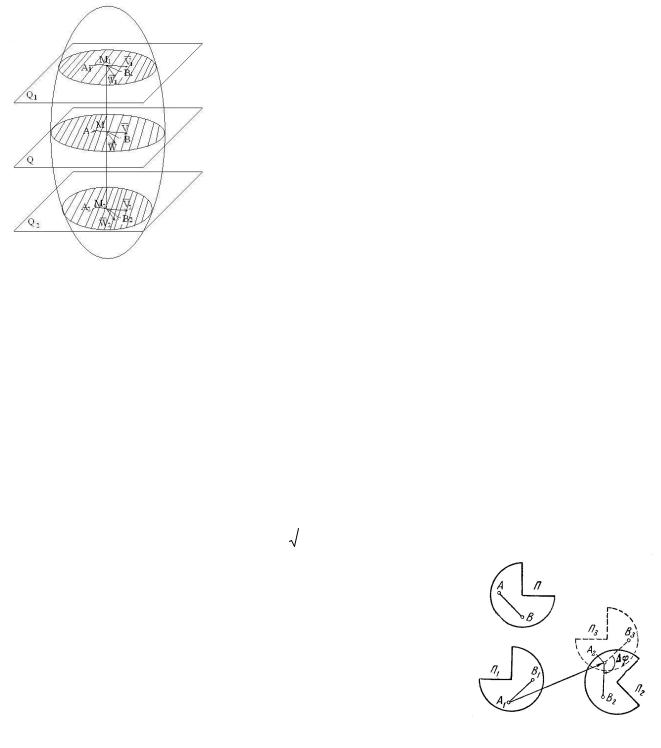
Теорема 1. Всякое перемещение плоской фигуры в ее плоскости может быть составлено из поступательного перемещения и поворота около произвольного центра (полюса)
(см. рис.).

Теорема 2. Всякое непоступательное перемещение плоской фигуры в ее плоскости может быть выполнено одним поворотом ее около определенного центра, называемого центром или полюсом конечного вращения (см. рис.).
Эти теоремы говорят о перемещении плоской фигуры из одного фиксированного положения в другое. Но, основываясь на них, можно представить геометрическую картину движения плоской фигуры.
Любое движение, в том числе и движение плоской фигуры в ее плоскости непрерывно и может рассматриваться как непрерывная последовательность элементарных перемещений, которую можно представить двумя способами.
1) Согласно Теореме 1 элементарное перемещение можно получить путем бесконечно малого поступательного перемещения вместе с произвольно выбранным полюсом и поворота на бесконечно малый угол вокруг этого полюса.
Отсюда следует, что всякое движение плоской фигуры можно рассматривать как совокупность поступательного движения, определяемого движением произвольно выбранного полюса, и вращательного движения вокруг этого полюса.
2) Согласно Теореме 2 любое элементарное перемещение фигуры можно осуществить одним только поворотом на бесконечно малый угол вокруг некоторого определенного центра, называемого мгновенным центром вращения. Следовательно, всякое непоступательное движение плоской фигуры можно рассматривать как непрерывную последовательность бесконечно малых поворотов вокруг мгновенных центров вращения (при этом положение мгновенного центра вращения непрерывно изменяется).
Поворот вокруг любого полюса или вокруг мгновенного центра происходит с одной и той
же для данного момента t угловой скоростью lim , (независящая от выбора полюса)
t 0 t
называется угловой скоростью фигуры в данный момент или мгновенной угловой скоростью. Мгновенный центр вращения – это предельное положение центра конечного вращения О, когда положение П2 стремится к положению П1. То есть это точка, элементарным поворотом
вокруг которой фигура перемещается из данного положения в соседнее, бесконечно близкое к данному.
Скорости всех точек А1, А2,…, Аn плоской фигуры в данный момент будут перпендикулярны к радиусам вращения
А1P, А2P,…, АnP. Скорость точки плоской фигуры, совпадающей с точкой P, будет в данный момент t равна нулю.
Эта точка фигуры называется мгновенным центром скоростей. Зная положение P, можно в данный момент времени t определить направление скорости любой точки плоской фигуры.
Чтобы определить положение мгновенных центров скоростей надо знать направление скоростей каких-нибудь двух точек фигуры. Восстановив перпендикуляры из этих точек, в их
пересечении получим мгновенный центр вращения P.
Центроиды. При движении плоской фигуры положение мгновенного центра вращения непрерывно изменяется как на неподвижной плоскости, так и на плоскости, связанной с движущейся фигурой. Геометрическое место мгновенных центров вращений на неподвижной плоскости есть непрерывная кривая, которая называется неподвижной центроидой. Геометрическое место мгновенных центров вращений на подвижной плоскости, связанной с движущейся фигурой есть
