УМК ТеорМех для Мех2012

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казахский национальный университет им. аль-Фараби

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Момент системы сил относительно центра.

Пусть F1,......,Fn - некоторая система сил.

Тогда вектор M0 , равный сумме моментов всех этих сил относительно центра О, т.е.

.pdf

Скачиваний:

Добавлен:

24.03.2015

Размер:

1.97 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

1.Реакция связи не вполне определяется самой связью; ее модуль, а иногда и направление, зависит от других сил и от движения системы (при отсутствии активных сил и движения реакции вообще не возникают). А модуль и направление активной силы известны заранее и от других приложенных к системе сил не зависят.

2.Активные силы могут сообщить системе то или иное движение (поэтому и называются

активными), а реакции связей – нет (поэтому пассивные силы).

Следовательно, всякое несвободное твердое тело можно освободить от связей, заменив действие связей их реакциями, и рассматривать его как свободное, находящиеся под действием приложенных к нему активных сил и реакций связей.

В статике связи, налагаемые на твердое тело, чаще всего встречаются в виде неподвижных поверхностей, линий, точек, гибких нитей.

Основные типы связей и их реакции

1.Идеальная гладкая неподвижная поверхность дает реакцию N к поверхности (рис.1).

2.Тело с гладкой поверхностью опирается на острие:

РеакцияN направлена по нормали к поверхности тела (т.е. если опорная поверхность вырождается в точку, то N направлена по к опирающейся поверхности) (рис. 2).

3.Двугранный угол. Реакции N1,N2 направлены по нормалям к гладким опорным поверхностям (рис. 3).

Рис. 1

Рис. 2

Рис. 3

4.Подвижный каток. Реакция N направлена по нормали к опорной поверхности (рис. 4).

5.Неподвижный цилиндрический шарнир (ось шарнира перпендикулярна плоскости Оху) (рис. 5а). Реакция R может иметь любое направление в плоскости Оху, перпендикулярной к его оси. Обычно реакция раскладывается на две составляющие по осям х и у (рис. 5б).

Рис. 4

Рис. 5

6.Шаровой шарнир (рис. 6) (или подпятник (рис.7)). Реакция R может быть какой угодно по модулю и направлению в пространстве. Обычно реакция раскладывается на три составляющие: по осям декартовой системы координат.

7. Невесомый стержень. Реакция R направлена вдоль оси стержня (рис. 8).

Рис. 6

Рис. 7

Рис. 8

8.Гибкое тело (нить, канат, цепь). Реакция направлена по нити и равна натяжению гибкой связи (рис. 9).

9.Жесткая заделка. Дает три реакции: по осям х, у и реактивный момент в плоскости Оху

(рис. 10).

Рис. 9

Рис. 10

Лекция 12

Система сил. Равнодействующая сил. Система сходящихся сил. Теорема о 3-х силах. Параллельные силы. Система многих параллельных сил. Центр параллельных сил. Статические моменты.

Система сил приложенных, в одной точке

Если на тело действуют две силы

приложенные в

одной

точке А,

то

равнодействующая этих сил

равна геометрической сумме

Модуль равнодействующей:

P2 Q2 2PQcos

P,Q

(перед косинусом стоит знак «плюс», хотя по теореме косинусов:

P2 Q2 2PQcos ,

но т.к. 1800 cos cos1800

cos ).

Направление

определяется

через

углы

По теореме sin:

sin

, где

sin

sin sin 1800 sin sin Q,P .

Если имеем систему n сил F1,..., Fn , приложенных в точке О, то применяя последовательно аксиому параллелограмма сил, получим:

R F1 ... Fn Fi

i 1

Таким образом, система сил, приложенных в одной точке, эквивалентна одной силе, т.е. имеет равнодействующую, равную геометрической сумме всех сил системы и приложенную в той же точке.

R может быть получена или графически аналитически:

	n	n	n
	Fix ,	Ry Riy ,	Rz Riz
Rx

(по методу векторного многоугольника) или

i 1

cos

; cos

;

cos

Равнодействующая системы сходящихся сил

Система действующих на абсолютно твердое тело сил, линии действия которых пересекаются в одной точке, называются системой сходящихся сил.

Очевидно, что можно перенести все силы по их линиям действия и приложить в одну точку О, следовательно система сходящихся сил приводится к равнодействующей, равной сумме этих сил и проходящую через точку О. Тогда для равновесия этой системы необходимо и

достаточно,

чтобы

равнодействующая

т.е.:

0 -

условие

равновесия

векторной форме.

i 1

В аналитической форме:

Rx Fix

0;Ry

Fiy

0;Rz Fiz

i 1

Т.к. при

силовой

многоугольник

замкнется, получаем

условие

равновесия

геометрической форме: для равновесия системы сходящихся сил необходимо и достаточно, чтобы векторный многоугольник, построенный из сил системы, был замкнутым.

Теорема о трех силах. Если плоская система трех непараллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.

Доказательство. Дано: F1,F2 ,F3 - плоская система сил в равновесии в точках A1, A2 , A3 .

Предположим, что линии действия F1 и F2 пересекаются в точке

О. Перенесем их в точку О и найдем R12 F1 F2 . Следовательно,

имеем эквивалентную систему F1,F2 ,F3 R12 ,F3 . Но система двух сил находится в равновесии только в том случае, если эти силы направлены по одной прямой, следовательно, линия действия F3

должна совпадать с линией действия R12 , т.е. должна пройти через точку О. Таким образом, для равновесия системы трех сил, лежащих в одной плоскости, необходимо (но недостаточно), чтобы линии действия этих сил пересекались

в одной точке.

Параллельные силы

Система двух параллельных сил, направленных в одну сторону и действующих на абсолютное твердое тело.

Рассмотрим систему двух параллельных сил, направленных в одну сторону и действующих

на абсолютно твердое тело. В точке А приложена сила P , в точке В - Q.

Соединяем точки А и В, приложим в точке А силуS , в точке

В силу

|=|

S |. Следовательно,

S ; |

Теперь сложим силы:

;

S =

. Система

3.Линии действия сил R1 и R2 пересекаются в точке О. Перенесем эти силы в точку О.

4.Разложим их в точке О R1 P S ; R2 Q S . Получим

систему сил

S , приложенных

в одной точке О.

0, следовательно, эти силы

можно отбросить. Остались две силы

направленные в одну сторону и действующие по одной прямой, параллельной линиям

действия P и Q. Их равнодействующая R P Q направлена параллельно данным силам.

5.Найдем, как линия действия R расположена по отношению к точкам А и В. Из подобия треугольников имеем:

P S , Q S .

OC AC OC CB

Разделим первое равенство на второе:

PCB P Q .

QAC CB AC

Таким образом, точка С AB и делит его внутренним образом на части, обратно пропорциональные силам.

Из последней пропорции составим:

P Q		P		Q	или	R		P		Q	. Отсюда легко определить AC , CB.
AC CB		CB		AC		AB		CB		AC

Система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, которая по модулю равна сумме модулей данных сил, параллельна им и направлена в ту же

сторону. Линия действия равнодействующей R проходит через точку, которая делит отрезокAB на части, обратно пропорциональные данным силам, внутренним образом.

Рассмотрим обратную задачу – о разложении R на две параллельные силы. Для определенности задачи необходимо задать модуль и линию действия одной силы, либо линии действия обеих сил.

1.Дается модуль и линия действия одной силы. Надо разложить равнодействующую так, чтобы одна сила была приложена в точке А и ее модуль равен P . Находим модуль второй

силы Q R P, а положение точки В из равенства:

CB AC

2. Даны равнодействующая

и положения точек

A,B,C

(т.е.

расстояния AC,BC ). Из

P R

равенства

Q R

Расстояние от точки С до линии действия силы называется плечом силы относительно точки С. Произведение силы на плечо – модуль величины, называемой моментом силы относительно данной точки.

Система двух антипараллельных сил (параллельные силы, направленные в

противоположные стороны).

Дано: в точке А приложена сила

, в точке B -

; P Q.

Разложим большую силу

на две параллельные силы

, причем так, чтобы |

|=|

и была приложена в точке В.

Тогда по известным формулам находим модуль

и ее точку

приложения С:

P R Q R P Q

Сила

и будет равнодействующей системы антипараллельных сил

. Действительно,

Система

двух

антипараллельных

сил

имеет

равнодействующую, которая равна по модулю разности модулей

этих сил, параллельна им и направлена в сторону большей силы. Линия действия R проходит через точку, которая лежит на продолжении AB и делит его внешним образом на части, обратно пропорциональные силам.

Обратная задача – разложение на две антипараллельные силы становится определенной в тех же случаях, что и для параллельных сил. Должны быть известны:

1.модуль и положение линии действия одной силы, либо

2.линии действия обеих сил.

Система многих параллельных сил

Если имеется система многих параллельных сил, то она приводится аналогичным образом к одной равнодействующей. Точка, через которую проходит равнодействующая системы параллельных сил, направленных в одну сторону, называется центром параллельных сил.

Центр тяжести

Сила, с которой тело притягивается к земле, называется силой тяжести. Численная

				величина этой силы равна весу тела.
					Рассмотрим небольшое, по сравнению с радиусом Земли, тело.
				Разобьем его на множество элементарных частиц. На каждую частицу
				действует сила тяжести, приложенная в точке, совпадающей с
				частицей. Все силы тяжести будут параллельны. Равнодействующая
				равна весу тела, а ее линия действия будет проходить через точку,
				совпадающую с центром параллельных сил тяжести частиц тела.
					Точка, являющаяся центром параллельных сил тяжести частиц
				тела, называется центром тяжести данного тела. Обозначается
				обычно через букву С.
					Пусть V - объем всего тела, V - объем какой-либо частицы, P -
				вес этой частицы.
Величина lim			P	dP	называется весом единицы объема тела в данной точке, а величина
Величина lim
		V 0	V dV
		представляет собой плотность тела (массу единицы объема) в данной точке.

	g
		Если тело однородно, то				и g - const. Вес любой частицы i с объемом Vi будет:
						Pi i Vi gi i Vi .

Если все силы тяжести частиц параллельны, то их равнодействующая равна сумме весов всех частиц, т.е. весу тела. Радиус-вектор точки приложения этой силы определяется как радиусвектор центра параллельных сил:

	Pi ri	i Vi ri .
r
c	Pi	i Vi

Так как i i gi , то

rc i gi Vi ri .i gi Vi

Если тело достаточно мало, то gi можно сократить, т.к. ускорение силы тяжести для всех точек тела будет одним и тем же. Тогда получим:

i Vi ri rc i Vi ,

где i Vi есть масса всего тела. Эта формула определяет радиус-вектор центра масс (центра

инерции) тела. Положение центра масс зависит только от распределения масс в объеме, занимаемом телом. Понятие центра масс – более общее, чем понятие центра тяжести. Кроме того, это понятие не связано с тем, находится тело в поле тяжести или нет. Для тела, находящегося в однородном поле тяжести, положение центра тяжести совпадает с положением центра масс.

Центр тяжести – геометрическая точка, она может не совпадать ни с какой точкой тела (к примеру – центр тяжести бублика).

Если и - непрерывные функции координат, то суммы представляют собой интеграл по объему.

Если тело однородно, то можно сократить:

r rdV - радиус-вектор центра тяжести объема тела.

c	V

Величина в числителе - rdV - называется статическим моментом относительно точки О.

Проекции статического момента на оси декартовой системы координат:

xdV

ydV

zdV

, zc

Если ищется центр масс плоских фигур, тогда вместо V берется S . Тогда вес частицы равен

, где

- вес единицы

площади.

Если тело однородно, то

rdS

Если ищется центр масс материальной линии,

то вместо V берется l. Тогда вес единицы

длины равна . Разобьем длину линии на элементы длины l . Тогда

lr .

Если линия однородна, то

rdl

Методы нахождения координат центра тяжести

1. Метод группировки. Разбиваем тело на части, центр тяжести которых легко определить, т.е можно найти:

i i

и т.д. Тогда, если в общей формуле

i 1

i 2

перегруппируем числитель, получим:

...

P1r1

P2 r2 ...

i 1

i i 2

, где P ,P ... веса соответствующих частей тела.

Симметрия. Если однородное тело имеет плоскость, ось или центра симметрии, то центр

тяжести этого тела находится соответственно в плоскости, на оси или в центре симметрии.

А). Пусть тело симметрично относительно плоскости xy. Тогда каждому элементу объема

тела

V x, y,z

соответствует

такой же по величине элемент

объема

V x, y, z .

статический момент относительно плоскости xy z V 0 zc

z V

0, т.е. zc xOy.

Б). Пусть тело симметрично относительно оси

z . Тогда каждому элементу объема тела

V x, y,z

соответствует такой же по величине элемент объема V x, y,z .

статические

x V 0

моменты

0, yc 0 zc 0. Следовательно, центр тяжести лежит на оси

y V 0

симметрии z .

В). Пусть тело имеет центр симметрии, который примем за начало координат О. Любой

частице тела с объемом V

соответствует такой же объем V

с радиус вектором

Следовательно,

статический момент относительно центра О r V

0 rc

0, т.е.

центр тяжести находится в центре симметрии.

3. Метод отрицательных масс. Это частный случай метода разбиения. Применяется к телам имеющим вырезы. Вырез рассматривается как площадь с отрицательной массой.

Лекция 13

Момент силы относительно центра и оси. Теория пар. Момент пары. Эквивалентность пар. Сложение пар. Теорема Вариньона.

Момент силы относительно центра

Пусть F - сила, приложенная в точке А (конец вектораF - в точке В), точка O - некоторый центр. Тогда моментом силы относительно центра O будет вектор, приложенный к центру O, направленный перпендикулярно к плоскости треугольника OAB в сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки и численно равный удвоенной

площади этого треугольника:

mom0F r F

Модуль этого вектора равен произведению F на расстояние h от центра O до линии

действия силы (h называется плечом силы относительно центра O), т.е. /r F / Fh

Если центр O принадлежит линии действия силы, то

mom0F 0 (т.к. h=0).

Если через центр O провести какую-нибудь систему прямоугольных осей Oxyz , то можно момент силы относительно центра представить в виде:


		i		j	k
mom0F r	F	x	y		z
		Fx	Fy		Fz

i 1

называется главным моментом системы этих сил относительно центра О. Если все силы

приложены в одной точке, то

n n

M0 (r Fi ) r Fi ,

i 1 i 1

отсюда следует что момент суммы сил, приложенных к одной точке, относительно какого-либо центра равен сумме моментов этих векторов относительно того же центра (теорема Вариньона).

Момент силы относительно оси. Моментом силы относительно оси называется

проекция момента силы, взятого относительно любой точки оси, на эту ось, т.е.

momx F (r F)x

Докажем, что точка O на оси x, относительно которой рассматривается

проекция момента силы F , может занимать любое положение на оси. Можно расписать:

momx

(

)

(

)

F остается константой,

(

)

есть также величина постоянная, равная

2S треугольника

с основанием

высотой

rsin(

0 ,

) d и,

следовательно, величина

(

)x не зависит от положения точки O.

Можно дать и другое определение.

Момент силы F относительно

какой-либо

оси x

– это момент проекции силы

F на

плоскость,

перпендикулярную к оси

x, взятый относительно точки O1

пересечения

оси x

с этой плоскостью. При этом момент проекции

A относительно

точки

рассматривается как

скалярная

величина. Если поворот,

совершаемый силой F A , виден с положительного конца оси х по часовой стрелке, момент берется со знаком «минус», если против часовой стрелки – со знаком «плюс»:

momx F momO1 FA FAh1 (скалярные величины).

Момент силы F относительно оси х равен нулю, если линия действия F пересекает ось x (в этом случае плечо h 0) или ей

параллельна (в этом случае проекция F A на плоскость равна нулю).

Проекции момента силы относительно осей декартовой системы координат могут быть расписаны следующим образом:

momx F (r F)x yFz zFy

momy F (r F)y zFx xFz

momz F (r F)z xFy yFx

Теория пар Моменты пары. Пара сил - это система двух равных по модулю

и противоположенных по направлению сил, действующих на твердое тело.

(F,F ) - пара, если F F , F F .

Расстояние d между линиями действия сил пары называется плечом пары. 1). Пара сил не имеет равнодействующей.

Пара сил, действующая на тело, стремится сообщить ему некоторое вращение. Вращательный эффект пары характеризуется моментом пары (момент равен F d ) и направлением вращения.

Момент пары (свободного вращения) есть вектор, перпендикулярный к плоскости действия пары, направленный по правилу правого винта и численно равный произведению одной из сил пары на плечо.

Эквивалентность пар.

Теорема 1. Действие пары на абсолютно твердое тело не изменится, если переместить пару в другое положение в плоскости ее действия.

Теорема 2. Действие пары на абсолютно твердое тело не изменится, если плоскость ее действия переносить параллельно самой себе.

Теорема 3. Действие пары на абсолютно твердое тело не изменится, если любым способом видоизменить силы и плечо пары, сохраняя постоянным их произведение, т.е. момент пары.

Сложение пар.

Теорема. Система пар, действующих на абсолютно твердое тело, эквивалентна одной паре, момент которой равен векторной сумме моментов этих пар.

Лекция 14

Система сил произвольно расположенных в пространстве. Приведение системы скользящих векторов (изложение со ссылкой на кинематику). Главный вектор и главный момент.

Лемма (основная). Всякая сила, приложенная к абсолютно твердому телу в данной точке А, эквивалентна той же силе, приложенной в другой точке В, и паре, момент который равен

моменту силы, приложенный в точке А, относительно точки В.

Доказательство. Пусть в точке А приложена сила FA . В точке В

приложим две взаимно противоположные силы FB FB , равные

по напряжению FA и параллельные ей. Тогда

FB и FA дают пару

с моментом, равным моменту данной силы

относительно точки

В, т.е.

A , что и требовалось доказать.

Приведение пространственной системы сил. Дана система произвольных сил:F1,.....,Fn . Выберем произвольную точку О и

перенесем в эту точку все силы. При этом каждая сила при переносе согласно основной лемме даст дополнительно пару, момент которой равен моменту Mi переносимой силы относительно

выбранного центра О. Складывая все силы, получим одну результирующую силу, которая называется главным вектором:

Fi R .

i 1

Складывая моменты всех пар, получим главный момент:

n n

(ri Fi ) Mi M0 .

i 1 i 1

Т.к. силы расположены произвольно в пространстве, то главный момент M0 по отношению

к R направлен под каким угодно углом. Таким образом, любая пространственная система сил, приведенная к некоторому центру О, заменяется одним главным вектором R , приложенным в точке О, и результирующей парой с главным моментом M0 .

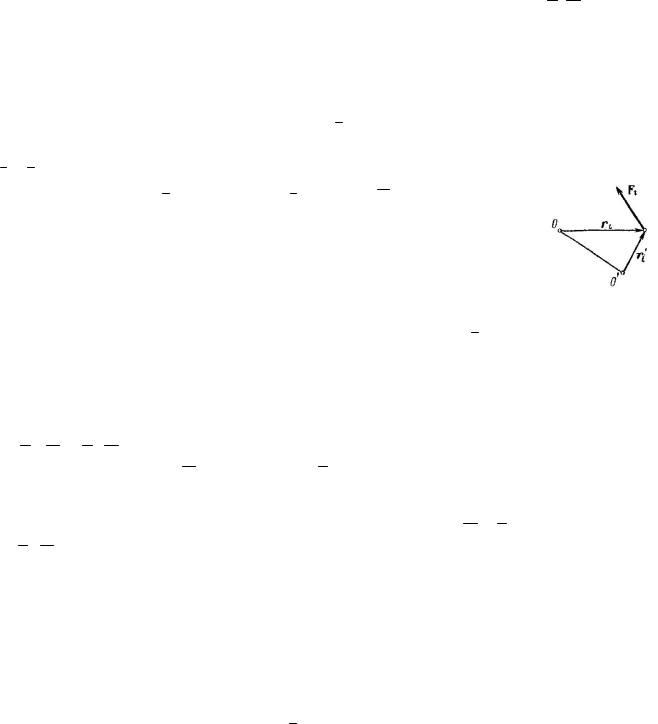
Изменение центра приведения. Пусть произвольная пространственная система сил приведена к центру О, при этом имеем главный вектор и главный момент -R,M0 . Возьмем произвольный другой центр O и приведем все силы системы к этому центру.

Очевидно, что R Fi

R (т.е. результирующая сила с изменением центра приведения

не изменяется – это первый инвариант системы). Найдем изменение

0 . Обозначим главный

момент относительно О через

, относительно O через

. Тогда

(

Радиус-вектор точки приложения

одной из сил

системы, проведенный

из нового центра:

. Подставляя это выражение, получим:

(

)

M OO

R M O O R . Т.е. главный момент

изменяется на величину, равную моменту вектора

относительно нового

центра приведения.

Вторым инвариантом

будет величина

или

RM RM cos(R,M)

проекция вектора

на направление

(

Доказательство: Для центра О мы имеем:

Для нового центра

: R

R Fi , M

M O O R

R(M

O O R) RM R (O O R).

Но R (O O R) равен нулю, т.к. имеет два

R) 0, т.к. sinO

равных множителя R (O O R) О О(R R) (R

R M R M const - второй инвариант.

Таким образом, проекция M на направление R - величина постоянная для данной системы сил и не зависит от выбора центра приведения.

Возможные расположения векторов M и R

1).R M 0

а)

0 (

лежит в плоскости пары (

которой заменим

). Система приводится к

одной силе, т.е. к равнодействующей

Это следует из того, что если R

M 0 p

б). R 0, но M 0 M M

const, т.к. M

M O O R 0. Т.е. главный момент не

зависит от выбора центра приведения. Система приводится к паре сил с моментом

(

) mom0

где О - произвольный центр.

в).

0 - система находится в равновесии.

2). Если

0, то любая система приводится к динаме (винту) с параметром

или к двум силам в разных плоскостях.

Динама (динамический винт) образуется главным

вектором

, направленным вдоль

центральной оси, и парой с наименьшим моментом

, коллинеарным

Две силы образуются, если вместо главного момента взять пару сил M (F,F ), одна из

которых проходит через точку О. Сложив главный вектор с этой силой, получим какую-то силу:

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.03.2015398.02 Кб77уголовное_1.rtf
#
24.03.2015741.42 Кб46Уголовное_2.rtf
#
24.03.2015240.64 Кб6угроза энерг безоп анализ.doc
#
24.03.2015495.67 Кб17Уильям Джеймс. Многообразие религиозного опыта.doc
#
08.03.2016367.18 Кб183УМК ХОМ.docx
#
24.03.20151.97 Mб19УМК ТеорМех для Мех2012.pdf
#
08.03.2016109.72 Кб46УМК ЭХМ.docx
#
04.05.2019448 Кб4УМКД - тексты 11-12.doc
#
08.03.2016607.39 Кб38УМКД по Соц-псих тренингу.docx
#
16.12.2018907.78 Кб7УП ЮРФАК.doc
#
24.03.20153.37 Mб172УПК РК Новый.doc