
- •Тема 2. Числа
- •Натуральные числа
- •Целые числа
- •Рациональные числа
- •Поле действительных чисел
- •Несоизмеримость диагонали квадрата и его стороны
- •Бесконечные десятичные дроби
- •Координаты на числовой оси
- •Сложение и умножение действительных чисел
- •Точные верхние и нижние грани
- •Степени и корни
- •Длина интервала на числовой прямой
- •Расширенная область действительных чисел
- •Пространство строк
Бесконечные десятичные дроби
Бесконечной десятичной дробью называют бесконечную сумму (т.е. ряд) вида

где
все
 – цифры, а впереди стоит либо знак «+»,
либо знак «-». При этом конечную десятичную
дробь
– цифры, а впереди стоит либо знак «+»,
либо знак «-». При этом конечную десятичную
дробь

назовем
приближением дроби (1) с точностью
 .
Знак «+» обычно опускают. Более кратко,
бесконечную десятичную дробь (1) записывают
как
.
Знак «+» обычно опускают. Более кратко,
бесконечную десятичную дробь (1) записывают
как

Например,
 .
.
Заметим, что рациональные числа изображаются периодическими бесконечными десятичными дробями. Например,

Для представления рационального числа в виде (периодической) бесконечной десятичной дроби мы просто делим уголком числитель на знаменатель. Для того, что бы представить периодическую десятичную дробь в виде рационального числа нужно воспользоваться теоремой о сумме геометрической прогрессии:

Формально,
соотношение (3) можно проверить, умножая
ряд
 на знаменатель
на знаменатель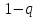 ,
раскрывая скобки и убеждаясь, что все
сокращается кроме 1. Вопросы сходимости
этого ряда и законности процедуры
умножения разобраны в главе «Ряды».
Например,
,
раскрывая скобки и убеждаясь, что все
сокращается кроме 1. Вопросы сходимости
этого ряда и законности процедуры
умножения разобраны в главе «Ряды».
Например,

Итак,
 .
По этой причине бесконечную дробь вида
.
По этой причине бесконечную дробь вида отождествляют с дробью
отождествляют с дробью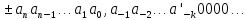 , где предполагается
, где предполагается и
и .
.
Определение.Действительным числом назовем
бесконечную десятичную дробь с
учетом описанного выше отождествления.
Совокупность действительных чисел
обозначим .
Числа из множества
.
Числа из множества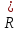 называют иррациональными.
называют иррациональными.
Например,
 ,
т.е.
,
т.е. -- иррационально, как было доказано
выше.
-- иррационально, как было доказано
выше.
Координаты на числовой оси
Мы
будем считать, что каждой точке
 на числовой прямой соответствует
координата
на числовой прямой соответствует
координата -- действительное число. При этом, если
-- действительное число. При этом, если лежит в положительном направлении от
начала координат, то
лежит в положительном направлении от
начала координат, то это не что иное как длина отрезка
это не что иное как длина отрезка .
Если же
.
Если же лежит в отрицательном направлении от
начала координат, то
лежит в отрицательном направлении от
начала координат, то .
.
Пусть
даны два действительных числа
 и
и ,
как координаты точек P и Q. Скажем, что
r<s тогда и только тогда, когда P лежит
левееQ
,
как координаты точек P и Q. Скажем, что
r<s тогда и только тогда, когда P лежит
левееQ
Сложение и умножение действительных чисел
Покажем
на примере
 ,
как складываются две бесконечные
десятичные дроби. Имеем:
,
как складываются две бесконечные
десятичные дроби. Имеем:

Складывая приближения с одним, двумя, тремя и т.д. десятичными знаками после запятой, получаем

Получаем
приближения бесконечной десятичной
дроби 3,146264369941972342…, которая и есть сумма
 .
Перемножаются бесконечные десятичные
дроби по тому же принципу – перемножают
их все более точные приближения, а затем
следят, к какой бесконечной десятичной
дроби стремятся эти приближения:
.
Перемножаются бесконечные десятичные
дроби по тому же принципу – перемножают
их все более точные приближения, а затем
следят, к какой бесконечной десятичной
дроби стремятся эти приближения:


Здесь
не так быстро как для сложения получаются
«верные» десятичные знаки. Три верных
знака мы получили лишь вычислив
произведение приближений с точностью
до

Умножение распространяется на все действительные числа при помощи правила знаков:

Теорема.Совокупность всех действительных чиселℝобразует поле относительно определенных выше операций сложения и умножения.
Отношение
 записывается также как
записывается также как .
Если
.
Если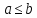 -- действительные числа, то
-- действительные числа, то


называют соответственно интервалом, отрезком и полуинтервалом.
Для неравенств выполняются такие правила
A.Если то
то
Б.Если ,
а
,
а то
то .
Если же
.
Если же ,
наоборот,
,
наоборот,
В.
Если или
или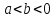 ,
то
,
то
С.(транзитивность отношения <) Если и
и ,
то
,
то
Наибольшее
из чисел
 будем обозначать
будем обозначать ,
а наименьшее --
,
а наименьшее -- .
.
Точные верхние и нижние грани
Подмножество
A поля действительных чисел называется
ограниченным сверху (снизу), если
найдется число
 ,
называемое верхней (нижней) границей
или гранью такое, что для любого
,
называемое верхней (нижней) границей
или гранью такое, что для любого следует
следует (∀
(∀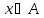 следует
следует ).
Ограниченное сверху и снизу множество
называют ограниченным. Верхняя грань
множества A называется точной верхней
гранью и обозначается
).
Ограниченное сверху и снизу множество
называют ограниченным. Верхняя грань
множества A называется точной верхней
гранью и обозначается ,
если она меньше любой другой верхней
грани.
,
если она меньше любой другой верхней
грани.
Аналогично определяется точная нижняя грань -- inf A.
Теорема о верхней грани. Любое непустое ограниченное сверху подмножество множества действительных чисел имеет точную верхнюю грань.
Теорема
о точной верхней грани в поле рациональных
чисел не выполняется как показывает
пример множества рациональных чисел
меньших
 ,
не имеющего точной верхней грани в
областиℚ.
,
не имеющего точной верхней грани в
областиℚ.
