Тема 4 Предел и непрерывность.

Предел числовой последовательности. Предел монотонной последовательности. Свойства предела. Предельный переход в неравенствах. Число e.

Предел функции. Свойства предела функции.

Замечательные пределы.

Непрерывность. Свойства непрерывных функций. Устойчивость знака.

Функции непрерывные на отрезке. Принцип непрерывности.

Предел последовательности вещественных чисел

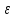Неравенство задает интервал, который называется𝜺-окрестностью точки (числа)Заметим, что любой интервал, содержащий точку, включает в себя-окрестность при достаточно малом

Определение.Числоназывается пределом последовательности(записывается), если для любого положительного𝜺найдется натуральное N такое, чтодля всех.

Пример.Докажем, что lim 1/n =0. Возьмём𝜺>0. Неравенство |1/n-0| <𝜺выполнено, если n>1/𝜺. В качестве N(𝜺) можно взять [1/𝜺]+1 -- наименьшее натуральное число, превосходящее 1/𝜺. Здесь через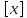обозначена целая часть числа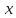, т.е. наибольшее целое число, не превосходящее.

Теорема.Любая монотонно возрастающая ограниченная сверху последовательностьимеет предел и он равен. Аналогично, любая монотонно убывающая и ограниченная снизу последовательность имеет предел равный точной нижней грани множества значений этой последовательности.

Доказательство. Пусть 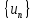-- монотонно возрастающая и ограниченная сверху последовательность. Обозначим. Пусть𝜺>0. Так как число u-𝜺не является верхней гранью значений нашей последовательности, то найдется натуральное N такое, что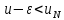. Тогда для любого n≥ N имеем

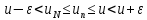
в силу монотонности последовательности и того факта, что u -- верхняя грань. Отсюда для любого натурального n≥ N следует неравенство<𝜺, что и требовалось доказать.□

Свойства предела

А.Если предел существует, то он единственен

Б.Предел суммы равен сумме пределов, если пределы слагаемых существуют.

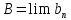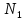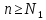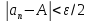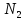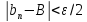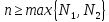Пусть ,. Фиксируем𝜺>0. Находимтакое, что для любоговыполняется неравенство. Аналогично, находимтакое, что для любоговыполняется неравенство. Тогда для любоговыполняется оценка

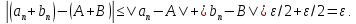
В.Предел константной последовательности равен этой константе

Последовательность 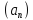называется ограниченной, если найдется константа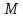такая, что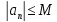для всех. Для доказательства следующего свойства нужна

Г. Любая сходящаяся последовательность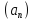ограничена.

Д.Предел произведения равен произведению пределов, при условии, что пределы сомножителей существуют.

Е.Константу можно выносить за знак предела:

Это утверждение есть следствие свойств Д и В.

Ж.Предел отношения равен отношению пределов, если пределы числителя и знаменателя существуют и последний не равен нулю.

На основе предела 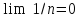можно вычислять другие пределы, пользуясь уже не определением, а правилами А-Е. Например,

Опишем теперь предельные переходы в неравенствах.

З.Если выполняется неравенство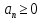начиная с некоторого N, и предел последовательности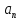существует, то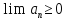. Аналогичное свойство имеет место для неравенства ≤ .

Действительно, если 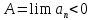, то длянайдется N, начиная с которого. Тогда.

Заметим, что для строгих неравенств аналогичное утверждение несправедливо. Например, 1/n>0 для любого n, но lim 1/n=0, как мы доказали выше.

И. Если выполняется неравенствоначиная с некоторого N, топри условии, что эти пределы существуют.

Действительно, так как 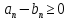для всех, то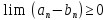согласно свойства Ж. Тогда, применяя свойства Б и Д, получим

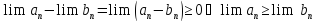
К (предел промежуточной последовательности). Если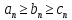начиная с некоторого номера, а пределы крайних последовательностей существуют и равны одному и тому же числу A, то предел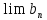также существует и равен A.