Тема 2. Числа

Натуральные числа. Цифры. Десятичная система счисления. Целые числа. Числовая ось. Порядок на кольце целых чисел. Рациональные числа, их равенство и арифметические операции, сравнение рациональных чисел. Десятичные дроби.

Поле действительных чисел как совокупность всех бесконечных десятичных дробей. Линейная упорядоченность поля 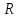. Полнота числовой прямой, аксиома о точной верхней грани. Приближения действительных чисел конечными десятичными дробями. Операции сложения и умножения над действительными числами. Координаты на числовой оси. Длина отрезка числовой оси.

Пополнение вещественной прямой бесконечно удаленными точками. Правила обращения с бесконечностью.

Числа бывают различной природы: натуральные -- ℕ, целые --ℤ, рациональные --ℚ, вещественные --ℝ, комплексные --ℂ. Каждая следующая система чисел есть расширение предыдущей:

ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ.

Натуральные числа

Натуральные числа, т.е. числа 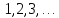получаются из единицы многократным применением операции сложения: 2=1+1; 3=2+1; …; 9=8+1;… Итак, множество натуральных чисел есть

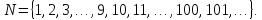
Множество натуральных чисел бесконечно. Первые девять натуральных чисел 1,2,…,9 и ноль 0 называются цифрами. При помощи цифр можно записать любое натуральное число, используя позиционную десятичную систему счисления:

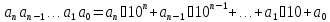
Здесь -- цифры. Пользуясь такой системой счисления, удобно столбиком складывать и умножать числа.

Геометрическая интерпретация натуральных чисел --точки на прямой ℓ, которые получаются в результате откладывания с помощью циркуля выбранного заранее единичного отрезка в выбранном направлении. Такой интерпретацией мы далее будем пользоваться постоянно, поэтому сформулируем

Определение.Числовой осью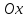называется прямая ℓ, с выбранной на ней точкой O (начало отсчета или начало координат), выбранном одном из двух положительном направлении и выбранном отрезке, длину которого полагаем равным единице. Противоположное направление к выбранному положительному направлению называется отрицательным направлением.

Итак, мы начали приписывать точке на оси координату– число. Сейчас мы это сделали только для некоторых точек – концов отрезков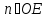. На множестве натуральных чисел вводится порядок: 1<2<3<… . Иными словами,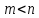для чисел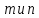, если и только если точкаP, соответствующая числуm(т.е.) лежит левее на числовой оси рис.1 чем точка Q, соответствующая числу n. Отношение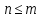нестрогого неравенства тогда получается из отношения строгого неравенства простой логической операцией: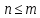по определению означает, что либо n=m, либо n<m. Например, 5 ≤ 5 -- верное высказывание.

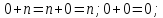
Присоединим к множеству натуральных чисел элемент ноль 0, обладающий свойствами для любого. Получаем множество всех целых неотрицательных чисел. Именно началу координат, точкеприпишем нулевую координату.

Целые числа

На множестве натуральных чисел уравнение вида не разрешимо, вообще говоря, относительно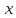. Чтобы исправить это, вводятся отрицательные целые числа. Это множество {-1,-2,-3,… }. Считаем, чтои, таким образом, по определению неравенство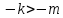для двух натуральных чисел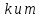имеет место тогда и только тогда, когда. Совокупность как положительных так и отрицательных целых чисел, а также нуля называется кольцом целых чиселℤ. Итак:

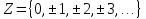
Целые отрицательные числа интерпретируются на числовой оси точками, которые получаются откладыванием единицы масштаба в отрицательном направлении (см. рис. 2)