
MATEMATIKA_EKZAMEN / ЛЕКЦИИ2 / Тема 6 Основные теоремы анализа
.docxТема 6 Основные теоремы анализа
-
Минимумы и максимумы
Пусть
функция
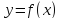 определена в окрестности точки
определена в окрестности точки
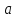 .
Точка
.
Точка
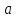 называется точкой локального максимума,
если
называется точкой локального максимума,
если
 для всех
для всех
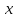 из достаточно малой окрестности точки
из достаточно малой окрестности точки
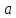 .
Если выполняется неравенство
.
Если выполняется неравенство
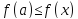 для всех
для всех
 из достаточно малой окрестности точки
из достаточно малой окрестности точки
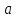 ,
то a называется точкой локального
минимума. Точка локального минимума
или локального максимума называется
точкой локального экстремума.
,
то a называется точкой локального
минимума. Точка локального минимума
или локального максимума называется
точкой локального экстремума.
Точек локального экстремума на заданном
отрезке может быть сколь угодно много
(в частности, бесконечно много). Значений
в этих точках может быть также сколь
угодно много. Но наибольшее (наименьшее)
значение функции на заданном множестве
может быть только одно. Каждая точка
интервала, в которой достигается
наибольшее значение (наименьшее значение)
на этом интервале автоматически будет
точкой локального максимума (локального
минимума), но обратное неверно (см. рис.).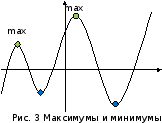
Теорема
Ферма; необходимое условие экстремума.
Пусть
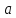 - точка локального экстремума функции
- точка локального экстремума функции
 ,
причем эта функция определена в
окрестности точки
,
причем эта функция определена в
окрестности точки
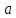 и имеет в этой точке производную. Тогда
и имеет в этой точке производную. Тогда
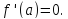
Доказательство.
Предположим, что
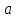 -- точка локального максимума. Тогда для
-- точка локального максимума. Тогда для
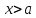 имеем
имеем
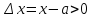 и
и
 .
Следовательно,
.
Следовательно,
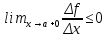 .
Но этот правый предел совпадает с
двусторонним пределом. Отсюда
.
Но этот правый предел совпадает с
двусторонним пределом. Отсюда
 .
Аналогично, рассматривая левый предел,
т.е. налагая условие
.
Аналогично, рассматривая левый предел,
т.е. налагая условие
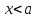 ,
получим, что
,
получим, что
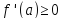 .
Из последних двух неравенств следует
равенство
.
Из последних двух неравенств следует
равенство
 .
□
.
□
Теорема
Ролля. Пусть функция
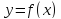 непрерывна на отрезке
непрерывна на отрезке
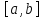 и дифференцируема на интервале
и дифференцируема на интервале
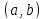 ,
а в концах отрезка
,
а в концах отрезка
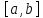 принимает одинаковое значение. Тогда
найдется точка
принимает одинаковое значение. Тогда
найдется точка
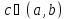 такая, что
такая, что
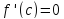 .
.
Доказательство.
Пусть
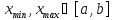 -- точки в которых функция
-- точки в которых функция
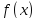 достигает своих наименьшего и наибольшего
значений (теорема Вейерштрасса). Если
достигает своих наименьшего и наибольшего
значений (теорема Вейерштрасса). Если
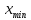 не является концевой точкой отрезка
не является концевой точкой отрезка
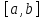 ,
то
,
то
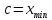 -- искомая точка по теореме Ферма.
-- искомая точка по теореме Ферма.
Аналогично
рассуждаем в случае, когда
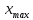 не является концевой точкой. Итак,
осталось разобрать случай, когда обе
точки
не является концевой точкой. Итак,
осталось разобрать случай, когда обе
точки
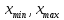 --
концевые. Тогда
--
концевые. Тогда
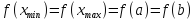 ,
и поэтому функция
,
и поэтому функция
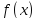 постоянна на отрезке
постоянна на отрезке
 ,
ибо любое значение
,
ибо любое значение
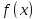 лежит между
лежит между
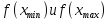 .
В этом случае в качестве c можно взять
любую точку интервала
.
В этом случае в качестве c можно взять
любую точку интервала
 .
□
.
□
Механический смысл теоремы Ролля: если материальная точка, двигаясь на оси, возвратилась в исходную точку, то найдется момент времени, в котором ее мгновенная скорость была равна нулю. Геометрический смысл теоремы Ролля состоит в том, что если концы гладкой кривой лежат на одном и том же уровне относительно некоторой прямой, то найдется точка на этой кривой, касательная в которой параллельна заданной прямой.
Теорема
Лагранжа. Пусть функция
 непрерывна на отрезке
непрерывна на отрезке
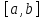 и дифференцируема на интервале
и дифференцируема на интервале
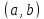 .
Тогда найдется точка
.
Тогда найдется точка
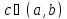 такая,
что
такая,
что

или
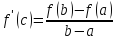
Доказательство.
Рассмотрим вспомогательную функцию
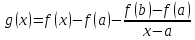 и применим к ней теорему Ролля. Это
можно сделать, так как
и применим к ней теорему Ролля. Это
можно сделать, так как
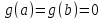 .
Тогда получаем точку
.
Тогда получаем точку
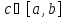 с условием
с условием
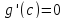 ,
т.е.
,
т.е.
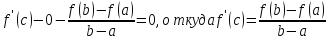
Механический смысл теоремы Лагранжа: -- если материальная точка движется на оси некоторый конечный отрезок времени, то найдется промежуточный момент времени, в котором ее мгновенная скорость была равна средней скорости. Геометрический смысл теоремы Лагранжа состоит в том, что если через концы гладкой кривой провести секущую ℓ , то найдется точка на этой кривой, касательная в которой параллельна прямой ℓ .
Обобщим теорему Лагранжа
Теорема
Коши. Пусть функции f(x) и g(x) непрерывна
на отрезке
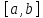 и дифференцируема на интервале (a,b),
причем g'(x)≠ 0 для любой точки
и дифференцируема на интервале (a,b),
причем g'(x)≠ 0 для любой точки
 .
Тогда найдется точка
.
Тогда найдется точка
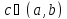 такая, что
такая, что
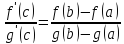
Доказательство
такое же как и у теоремы Лагранжа, но
следует взять вспомогательную функцию
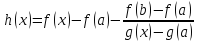 .
.
-
Правило Лопиталя
Теорема.
Пусть функции
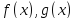 дифференцируемы в окрестности точки
дифференцируемы в окрестности точки
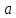 и
и
 .
Предположим также, что
.
Предположим также, что
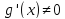 в некоторой достаточно малой проколотой
окрестности точки
в некоторой достаточно малой проколотой
окрестности точки
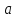 .
Если существует предел отношения
производных
.
Если существует предел отношения
производных
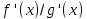 при
при
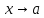 ,
то существует предел отношения функций,
и эти два предела совпадают:
,
то существует предел отношения функций,
и эти два предела совпадают:
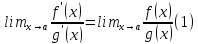
Доказательство. Имеем
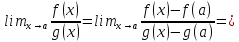
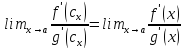
Здесь
мы применили теорему Коши к отрезку
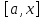 и нашли точку
и нашли точку
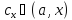 .□
.□
Правило
Лопиталя для бесконечности. Пусть
функции
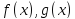 дифференцируемы для всех достаточно
больших
дифференцируемы для всех достаточно
больших
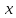 .
Предположим также, что
.
Предположим также, что
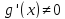 для всех достаточно больших
для всех достаточно больших
 .
Если
.
Если
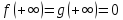 и существует предел отношения производных
и существует предел отношения производных
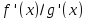 при
при
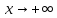 , то существует предел отношения функций
и эти два предела совпадают:
, то существует предел отношения функций
и эти два предела совпадают:
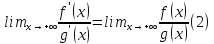
Аналогичный результат имеет место и для -∞ .
Замена
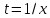 сводит доказательство к случаю a=0 правила
Лопиталя.
сводит доказательство к случаю a=0 правила
Лопиталя.
Правило
Лопиталя для неопределенности ∞/∞ .
Пусть функции
 дифференцируемы для всех достаточно
больших
дифференцируемы для всех достаточно
больших
 .
Предположим также, что
.
Предположим также, что
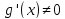 для всех достаточно больших x. Если
для всех достаточно больших x. Если
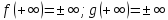 и существует предел отношения производных
и существует предел отношения производных
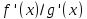 при x→ +∞ , то существует
предел отношения функций и эти два
предела совпадают (см (2)).
при x→ +∞ , то существует
предел отношения функций и эти два
предела совпадают (см (2)).
Аналогичный результат имеет место и для -∞ .
Замена дроби f/g на (1/g)/(1/f) сводит доказательство к предыдущему случаю.
Пример.
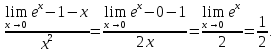
-
Сравнение степени возрастания показательных, степенных и логарифмических функций.
Для
любого
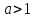 и для любого натурального n имеет место
соотношение
и для любого натурального n имеет место
соотношение
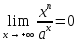
а также соотношение

Для
доказательства этих соотношений следует
применить правило Лопиталя достаточно
количество раз. Эти соотношения
обобщаются на случай, когда
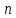 -- любое действительное число.
-- любое действительное число.
Пример.
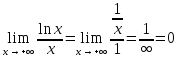
-
Формула Тейлора
Ставится
задача приблизить (аппроксимировать)
функцию
 в окрестности точки
в окрестности точки
 многочленом степени n. Для n=1 мы уже нашли
решение:
многочленом степени n. Для n=1 мы уже нашли
решение:
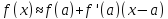 .
Удобно точкой отсчета считать нулевую
точку, т.е. от координат
.
Удобно точкой отсчета считать нулевую
точку, т.е. от координат
 мы переходим к приращениям
мы переходим к приращениям
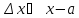 и
и
 .
Ряд
.
Ряд
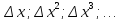
представляется из себя семейство бесконечно малых величин, каждая последующая из которых есть б.м. большего порядка, чем предыдущая. Поставим задачу о разложении вида
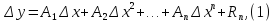
где
остаточный член
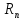 есть б.м. высшего порядка по сравнению
с
есть б.м. высшего порядка по сравнению
с
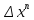 .
Деля (1) на
.
Деля (1) на
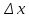 и устремляя
и устремляя
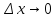 получаем
получаем
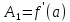 .
Найдем другие коэффициенты в этом
разложении:
.
Найдем другие коэффициенты в этом
разложении:
Локальная
формула Тейлора. Пусть функция
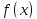 дифференцируема в окрестности точки
дифференцируема в окрестности точки
 n раз, и n-ая производная непрерывна в
точке
n раз, и n-ая производная непрерывна в
точке
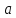 .
Тогда
.
Тогда
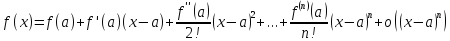
Доказательство. Применяем n раз правило Лопиталя к вычислению предела отношения
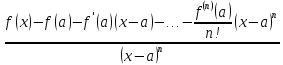 и доказываем, что этот предел равен 0.□
и доказываем, что этот предел равен 0.□
В
условиях теоремы функция
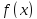 раскладывается
в окрестности точки a в сумму многочлена
степени ≤ n от переменной
раскладывается
в окрестности точки a в сумму многочлена
степени ≤ n от переменной
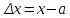 и остаточного члена
и остаточного члена
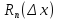 ,
про который известно, что он есть величина
бесконечно малая высшего порядка по
сравнению с
,
про который известно, что он есть величина
бесконечно малая высшего порядка по
сравнению с
 .
.
Функция
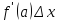 линейна по переменной
линейна по переменной
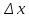 ,
она называется дифференциалом
,
она называется дифференциалом
 в точке
в точке
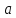 и обозначается
и обозначается
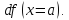 Легко видеть, что
Легко видеть, что
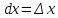 .
Мы получаем «симметричный» вид
дифференциала вычисленный в произвольной
точке
.
Мы получаем «симметричный» вид
дифференциала вычисленный в произвольной
точке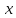 :
:

Отсюда
получаем, что производная равна отношению
дифференциалов:
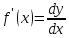
Аналогично,
функция
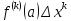 называется дифференциалом k-го
порядка и обозначается
называется дифференциалом k-го
порядка и обозначается
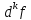 .
Ее симметричный вид есть
.
Ее симметричный вид есть
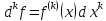 .
Тогда локальная формула Тейлора в
дифференциалах принимает вид:
.
Тогда локальная формула Тейлора в
дифференциалах принимает вид:
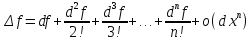
Уточним вид остаточного члена
Формула
Тейлора с остаточным членом в форме
Лагранжа. Пусть функция
 дифференцируема
в окрестности точки
дифференцируема
в окрестности точки
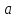 n+1 раз. Тогда для всех
n+1 раз. Тогда для всех
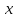 достаточно близких к
достаточно близких к
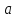 найдется точка
найдется точка
 такая, что
такая, что

В частности, если

то имеет место следующая оценка остаточного члена:

Частный
случай формулы Тейлора -- формула
Маклорена получается при
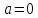 .
Тогда при наличии n+1 производной в
окрестности нуля, для каждого достаточно
малого
.
Тогда при наличии n+1 производной в
окрестности нуля, для каждого достаточно
малого
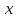 найдется
найдется
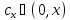 такой, что
такой, что
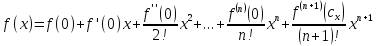
-
Разложение элементарных функций по формуле Маклорена
-
Разложение экспоненты
Для всех x∈ ℝ имеет место разложение
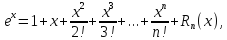
где
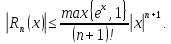
Например,
если
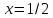 ,
то
,
то
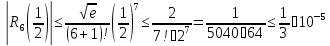
Тем
самым
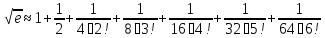 c точностью
c точностью
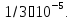
-
Разложение синуса и косинуса
Для
всех
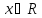 имеет место разложение
имеет место разложение

где

Для
всех
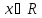 имеет место разложение
имеет место разложение

где
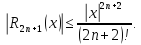
-
Бином Ньютона
Для
каждого действительного числа α и для
каждого
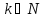 определим биномиальный коэффициент
определим биномиальный коэффициент

По
определению полагаем также, что
 .
Имеем:
.
Имеем:
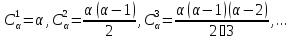
Теорема.
Для любого действительного α и для
любого
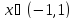 имеет место разложение
имеет место разложение
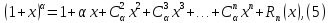
причем
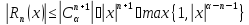
Рассмотрим частные случаи формулы (5).
Случай
α =m -- натуральное число. Тогда
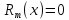 и мы получаем бином Ньютона
и мы получаем бином Ньютона
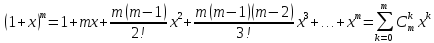
Случай
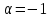 .
Тогда нетрудно вывести, что
.
Тогда нетрудно вывести, что
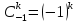 .
Поэтому
.
Поэтому
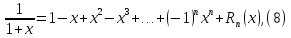
где
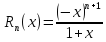
-
Разложение логарифма
Из (8) или непосредственно нетрудно получить
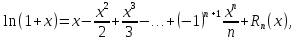
где

