
MATEMATIKA_EKZAMEN / ЛЕКЦИИ2 / Тема 9 Векторы
.docxВекторы
-
Основные определения векторного исчисления
-
Понятие вектора
-
Вектором
называется направленный отрезок, т. е.
отрезок
 ,
одна крайняя точка которого (скажем
,
одна крайняя точка которого (скажем
 )
объявлена началом, а другая концом.
Такой вектор обозначается как
)
объявлена началом, а другая концом.
Такой вектор обозначается как
 .
Длиной или модулем вектора
.
Длиной или модулем вектора
 называется длина отрезка
называется длина отрезка
 ;
она обозначается как
;
она обозначается как
 .
Примерами векторных величин является
скорость, ускорение, сила, перемещение.
Если
.
Примерами векторных величин является
скорость, ускорение, сила, перемещение.
Если
 ,
то вектор
,
то вектор
 называется нулевым и обозначается 0.
Вектора, два или более, называются
коллинеарными, если прямые, на которых
они лежат, либо параллельны, либо
совпадают. Два вектора
называется нулевым и обозначается 0.
Вектора, два или более, называются
коллинеарными, если прямые, на которых
они лежат, либо параллельны, либо
совпадают. Два вектора
 и
и
 называются равными, если их длины равны,
они коллинеарны и сонаправлены, т. е.
"смотрят" в одну сторону (см. рис.
1). Если вектора
называются равными, если их длины равны,
они коллинеарны и сонаправлены, т. е.
"смотрят" в одну сторону (см. рис.
1). Если вектора
 и
и
 не лежат на одной прямой, то их равенство
эквивалентно тому, что четырехугольник
не лежат на одной прямой, то их равенство
эквивалентно тому, что четырехугольник
 есть параллелограмм.
есть параллелограмм. 
Простое
геометрическое построение убеждает
нас, что для любого вектора
 и любой точки
и любой точки
 существует единственная точка
существует единственная точка
 такая, что
такая, что
 .
Этот вектор
.
Этот вектор
 называется реализацией вектора
называется реализацией вектора
 в точке
в точке
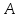 .
.
-
Арифметические операции над векторами
Пусть
имеются два вектора
 .
Реализуем
.
Реализуем
 в точке A:
в точке A:
 ,
а вектор
,
а вектор
 реализуем в точке B:
реализуем в точке B:
 .
Тогда вектор
.
Тогда вектор
 назовем суммой векторов
назовем суммой векторов
 . Это определение корректно, т. е. результат
суммы двух векторов не зависит от
изначально выбранной точки
. Это определение корректно, т. е. результат
суммы двух векторов не зависит от
изначально выбранной точки
 .
Из определения суммы векторов вытекает
равенство Шаля:
.
Из определения суммы векторов вытекает
равенство Шаля:

Равенство Шаля можно обобщить на случай многих векторов:


Существует
другое определение операции суммы двух
векторов -- правило параллелограмма,
но оно "работает" только для не
коллинеарных векторов. Пусть имеются
два неколлинеарных вектора
 .
Реализуем их в одной точке A, так что
.
Реализуем их в одной точке A, так что
 и
и
 .
Достроим
.
Достроим
 до параллелограмма
до параллелограмма
 .
Тогда
.
Тогда
 (см. рис. 2). Результат сложения не зависит
от выбора точки
(см. рис. 2). Результат сложения не зависит
от выбора точки
 .
Так как
.
Так как
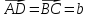 на рис. 2, то сложение по правилу
параллелограмма приводит к тому же
результату, что и сложение по правилу
треугольника.
на рис. 2, то сложение по правилу
параллелограмма приводит к тому же
результату, что и сложение по правилу
треугольника.
Умножить
вектор
 на число
на число
 значит построить вектор
значит построить вектор
 такой, что
такой, что
-

-

-
если
 ,
то
,
то
 и
и
 сонаправлены, а если
сонаправлены, а если
 ,
то
,
то
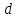 и
и
 направлены в противоположные стороны.
В случае
направлены в противоположные стороны.
В случае
 вектор
вектор
 нулевой.
нулевой.
 Вектор
Вектор
 можно реализовать прямой ℓ в точке
можно реализовать прямой ℓ в точке
 как вектор
как вектор
 ,
где точка
,
где точка
 строиться
так, что
строиться
так, что
 ,
причем, если >0,
то точка D должна лежать по ту же сторону
от A, что и точка B; если же
<0, то точку D следует выбирать на прямой
ℓ по другую сторону от (см. рис. 3).
,
причем, если >0,
то точка D должна лежать по ту же сторону
от A, что и точка B; если же
<0, то точку D следует выбирать на прямой
ℓ по другую сторону от (см. рис. 3).
Заметим,
что из определения умножения вектора
на число вытекает, что вектор
 коллинеарен ненулевому вектору
коллинеарен ненулевому вектору
 тогда и только тогда, когда
тогда и только тогда, когда
 для подходящего числа
для подходящего числа
 .
.
Множество всех векторов в пространстве, относительно определенных выше операций сложения и умножения обладает следующими свойствами:
-
 (коммутативность);
(коммутативность); -
 (ассоциативность);
(ассоциативность); -
 (свойство
нейтральности нулевого вектора
относительно операции сложения);
(свойство
нейтральности нулевого вектора
относительно операции сложения); -
для любого вектора
 существует противоположный вектор
существует противоположный вектор
 такой, что
такой, что
 ;
;
-
 (ассоциативность
умножения);
(ассоциативность
умножения); -
 и
и
 (дистрибутивность);
(дистрибутивность); -
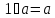 (унитарность).
(унитарность).
Эти равенства
верны для любых векторов
 и любых действительных чисел
и μ .
и любых действительных чисел
и μ .
-
Разложение по стандартному базису
Рассмотрим
в пространстве декартову систему
координат
 .
Обозначим через
.
Обозначим через
 вектора единичной длины, направленные
по осям
вектора единичной длины, направленные
по осям
 соответственно. Эту упорядоченную
тройку векторов называются стандартным
базисом (см. рис.). Этот набор векторов
ортонормирован в том смысле, что
соответственно. Эту упорядоченную
тройку векторов называются стандартным
базисом (см. рис.). Этот набор векторов
ортонормирован в том смысле, что

Стандартный
базис на плоскости состоит из двух
векторов
 .
.
Теорема.
Для любого вектора
 существуют единственный набор чисел
существуют единственный набор чисел
 называемый координатами вектора
называемый координатами вектора
 относительно стандартного базиса и
такой, что
относительно стандартного базиса и
такой, что
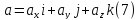
Доказательство.
Сначала заметим, что если
 -- параллелепипед с основанием
-- параллелепипед с основанием
 ,
то
,
то


Итак, пусть
нам дан произвольный вектор
 реализованный в начале координат.
Опустим перпендикуляры из конца вектора
реализованный в начале координат.
Опустим перпендикуляры из конца вектора
 ,
точки
,
точки
 на оси
на оси
 . Получим точки
. Получим точки
 соотвественно. Достроим пирамиду
соотвественно. Достроим пирамиду
 до прямоугольного параллелепипеда
до прямоугольного параллелепипеда
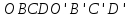 и применим соотношение (8):
и применим соотношение (8):
 .
Так как
.
Так как
 ,
то
,
то
 для подходящего и единственным образом
определенного числа
для подходящего и единственным образом
определенного числа
 (см. замечание после определения
произведения вектора на число). Аналогично,
(см. замечание после определения
произведения вектора на число). Аналогично,
 и
и
 .
Собирая все вместе, получаем (7) □
.
Собирая все вместе, получаем (7) □
В координатах
арифметические операции над векторами
выражаются следующим образом. Пусть
вектора имеют координаты
имеют координаты
 и
и
 соответственно. Тогда координаты
векторов
соответственно. Тогда координаты
векторов
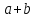 и
и
 будут
будут

соответственно.
Вектор
можно проектировать на плоскость и
прямую. Пусть заданы вектор
 и прямая или плоскость
и прямая или плоскость
 Проекции точек
Проекции точек
 на
на
 обозначим
обозначим
 .
Тогда вектор
.
Тогда вектор
 назовем проекцией вектора
назовем проекцией вектора
 на прямую (плоскость)
на прямую (плоскость)
 .
Это определение корректно, т.е. результат
не зависит от реализации вектора
.
Это определение корректно, т.е. результат
не зависит от реализации вектора
 .
Более того, проекция обладает свойством
линейности:
.
Более того, проекция обладает свойством
линейности:

Теорема.
Пусть
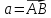 и известны координаты точек
и известны координаты точек
 и
и
 –
–
 и
и
 соответственно. Тогда
соответственно. Тогда

Доказательство.
Имеет место равенство
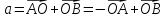 .
Из определения координат вектора
вытекает, что координаты вектора,
реализованного в начале координат,
совпадают с координатами концевой
точки. Следовательно,
.
Из определения координат вектора
вытекает, что координаты вектора,
реализованного в начале координат,
совпадают с координатами концевой
точки. Следовательно,
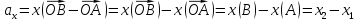
Аналогично доказываются оставшиеся два равенства. □
-
Орт и направляющие косинусы
Длина
вектора
 выражается через его координаты следующим
образом
выражается через его координаты следующим
образом

Этоа формула есть простое следствие теоремы Пифагора.
Пусть
 - углы, которые образует ненулевой
вектор
- углы, которые образует ненулевой
вектор
 с осями
с осями
 соответственно. Тогда
соответственно. Тогда
 назовем направляющими косинусами
вектора
назовем направляющими косинусами
вектора
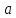 .
.
Вектор,
сонаправленный с вектором
 ,
и имеющий единичную длину, назовем
ортом и обозначим
,
и имеющий единичную длину, назовем
ортом и обозначим
 .
.
Нетрудно
видеть, что, если
 -- ненулевой вектор, то координаты орта
-- ненулевой вектор, то координаты орта
 имеют вид
имеют вид
 ,
причем они совпадают с направляющими
косинусами вектора
,
причем они совпадают с направляющими
косинусами вектора
 :
:

Зная длину и направляющие косинусы, можно найти координаты вектора по формулам

-
Скалярное произведение геометрических векторов
Скалярным
произведением векторов
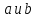 называется произведение длин этих
векторов на косинус угла между ними:
называется произведение длин этих
векторов на косинус угла между ними:

Если один из векторов нулевой, то и скалярное произведение равно 0.
Это
произведение называется скалярным,
поскольку двум векторам сопоставляется
число -- скалярная величина. Отметим
свойства скалярного произведения. Сразу
из определения следует (СК2) симметричность:
скалярное произведение не зависит от
порядка сомножителей:
 .
.
Скалярным
квадратом называется скалярное
произведение вектора на самого себя:
 .
Имеет место положительная определенность
и невырожденность скалярного произведения:
если
.
Имеет место положительная определенность
и невырожденность скалярного произведения:
если
 ,
то
,
то
 .
.
В частности, длина вектора выражается через скалярное произведение следующим образом:

Угол между ненулевыми векторами также выражается через скалярное произведение, ибо

Если векторы ортогональны, т. е. лежат на перпендикулярных прямых, то скалярное произведение равно нулю. Очевидно, верно и обратное утверждение. Таким образом, мы получаем критерий ортогональности:

В частности, имеет место ортонормированность стандартного базиса:

СК1. Билинейность:


Действительно,
равенство
 верно в силу симметричности скалярного
произведения, а равенство
верно в силу симметричности скалярного
произведения, а равенство
 доказывается, как и выше:
доказывается, как и выше:
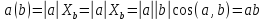
Вычисление
скалярного произведения в координатах.
Если
 и
и
 ,
то
,
то

Доказательство. Применяем билинейность и учитываем (4).
Следствие.
Если вектора
 ненулевые, то
ненулевые, то

В частности,
вектора
 ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда

-
Векторное произведение
Тройку
векторов
 назовем правой, если определитель
назовем правой, если определитель

строго
больше нуля. Если этот определитель
меньше нуля, то тройку векторов
 назовем левой.
назовем левой.
Определение.
Векторным произведением вектора
 на вектор
на вектор
 называется вектор, обозначаемый
называется вектор, обозначаемый
 такой, что
такой, что
1) он
перпендикулярен плоскости векторов
 ;
;
2) длина
этого вектора равна площади параллелограмма,
построенного на векторах
 ,
т.е.
,
т.е.
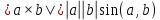
3) тройка
векторов
 правая
правая
Третий
пункт в определении векторного
произведения можно выразить таким
наглядным способом: глядя из конца
вектора
 ,
вращение от
,
вращение от
 кажется происходящим против часовой
стрелки.
кажется происходящим против часовой
стрелки.
Если
 -- вектор силы, а
-- вектор силы, а
 -- вектор, описывающий рычаг, на конец
которого действует сила
-- вектор, описывающий рычаг, на конец
которого действует сила
 ,
то векторное произведение
,
то векторное произведение
 дает момент силы a относительно
начала вектора
дает момент силы a относительно
начала вектора
 .
.
Свойства векторного произведения:
ВП1.
Билинейность --
 и
и

ВП2.
Кососимметичность:
 для всех векторов
для всех векторов
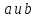
ВП3.
 .
.
Вычисление
векторного произведения в координатах.
Если
 и
и
 ,
то
,
то
 (2)
(2)
Следствие.
Площадь параллелограмма, построенного
на векторах
 равна
равна

В частности,
если
 -- вектора на плоскости, то
-- вектора на плоскости, то

Это можно
трактовать как геометрический смысл
определителя
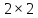 .
.
