Непрерывность на отрезке

Теорема Вейерштрасса.Функция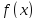, непрерывная на отрезке, ограничена на этом отрезке и достигает своего наибольшего и наименьшего значения, т.е. существуют точки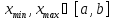такие, что

для любого .

Для интервала аналогичное утверждение неверно -- см. пример неограниченной функции tgxна интервале (-π /2,π /2).

Теорема Больцано-Коши.Пусть функциянепрерывна на отрезке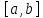и в концах отрезка принимает значения разных знаков. Тогда найдется точкатакая, чтоf(c)=0.

Следствие. Пусть функциянепрерывна на отрезке. Обозначим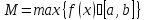,. Тогда для любого числаCлежащего междуmиMнайдется точкатакая, что.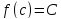

Достаточно применить теорему Больцано-Коши к разности и отрезкувместо.

Определение.Функцияназывается обратной к функции, еслии.

Например, обратна к функции. Немного не строго, в ситуации предыдущего определения, функциютакже называют обратной к функции.

Теорема [непрерывность обратной функции]. Еслинепрерывно и строго монотонно отображает отрезокв отрезоктак, что(либов случае убывающей функции), то обратная функциясуществует, и она непрерывно и монотонно отображает отрезокна отрезок.

Доказательство. Существование обратной функции, т.е. фактически свойство , вытекает из следствия теоремы Больцано-Коши. Монотонностьgясна.

Пустьи𝜺>0. Предполагаем, чтовозрастает. Тогда

Возьмем

.

Тогда для выполняется неравенство. Это влечет непрерывность функцииg.□

Ранее мы уже определили корень арифметический n-ой степени из неотрицательного числа. Однако непрерывность корня мы можем обосновать только сейчас.

Следствие.Существует и единственен арифметический корень-- непрерывная функция как обратная к непрерывной монотонной функции.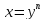

Принцип непрерывности

Ранее мы определили и частично изучили степенные функции , тригонометрические, показательныеи логарифмические. Добавим сюда еще обратные тригонометрические функции

Все перечисленные выше функции называются основными элементарными функциями.

Функция называется элементарной, если она может быть получена из основных элементарных функций действиями сложения, вычитания, умножения, деления и подстановкой функции в функцию. Так, например -- элементарные функции. Однако существуют очень важные функции, не являющиеся элементарными. Таковыми, например, являются функция ошибок и интегральный синус.

Теорема. Любая элементарная функция непрерывна на всей естественной области определения.

Доказательство. Ранее доказана непрерывность многочленов, . Непрерывностьпримем на веру. Непрерывностьследует из свойства Н4 (§Непрерывность функции). Тогда и-- непрерывные функции (там, где они определены), как частное двух непрерывных функций (свойство Н3). Следовательно,непрерывны как обратные функции к непрерывным монотонным функциям. В силу свойств непрерывных функций Н1-Н4 и определения элементарной функции, получаем, что любая элементарная функция непрерывна.□

16