8. Непрерывность функции

Определение.Функция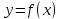, определенная в окрестности точки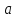,называется непрерывной в этой точке, если. Функция непрерывна на отрезке (интервале), если она непрерывна в каждой точке этого отрезка (интервала).

Это определение можно переписать так: функция непрерывна в точке 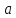, если

,

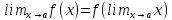т.е. когда две операции над переменной 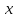-- функцияfи предельный переход перестановочны.

Обозначим 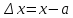--приращение переменнойи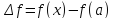--приращение функции. Тогда определение непрерывности можно переписать и так: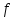непрерывна в точкеa, если.

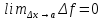1. Свойства непрерывных функций

Н1.Сумма непрерывных функций есть непрерывная функция

Н2.Произведение непрерывных функций есть непрерывная функция

Н3.Частное непрерывных функций -- непрерывная функция, во всех точках, где знаменатель отличен от 0

Эти свойства являются непосредственным следствием соответствующих свойств пределов (см. LIM2-LIM4, ).

Н4.Подстановка непрерывной функции в непрерывную функцию есть непрерывная функция

Это свойство следует из свойства LIM8 -- предел сложной функции.

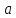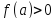Устойчивость знака непрерывной функции.Пустьнепрерывна в точке, и. Тогда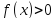для всех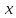достаточно близких к.

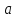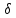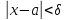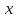Доказательство. Для найдетсятакое, что как только, то. Для этих значенийимеем:□

Примеры непрерывных функций

1. Константа, а также тождественная функция 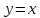непрерывны.

Доказательство вытекает из LIM1.

2. Любой многочлен непрерывная функция.

Применяем Н1 и Н2 к тождественной функции

3. Рациональная функция, т.е. отношение двух многочленов, непрерывная функция в точках не являющихся корнями знаменателя.

Применяем Н3 к многочленам.

4. Функция 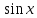непрерывна.

Действительно, (применяем неравенство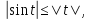полученное при выводе первого замечательного предела). Отсюда следует, что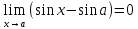, т.е.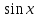непрерывна в точке.

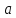5. Функция 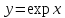непрерывна. Действительно,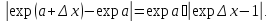

и при достаточно малых 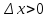имеет место оценка:

???

9. Непрерывность на отрезке

Лемма 1. Из ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство. Из ограниченности последовательности вытекает, что все ее значения принадлежат отрезку. Делим этот отрезок пополам и выбираем ту половину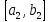, в которой бесконечное число членов последовательности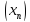(если обе половины удовлетворяют этому условию, то выбираем, например, левую). С отрезком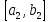поступаем точно также. Получаем систему вложенных друг в друга отрезков, которые по принципу Кантора о вложенных отрезках имеет общую точкуd. Выберем затем индексы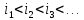так, что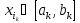. Тогда в силу, для любого𝜺>0 окрестность (d-𝜺,d+𝜺) содержит все отрезки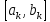а значит и все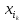начиная с некоторого номераN. Это доказывает, что.□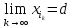

Лемма 2 [замкнутость отрезка]Отрезок содержит все свои предельные точки.

Доказательство. Если все 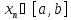, то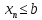для всехn. Отсюда получаем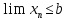. Аналогично,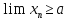. Тогда.□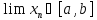

Теорема Вейерштрасса.Функция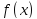, непрерывная на отрезке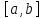, ограничена на этом отрезке и достигает своего наибольшего и наименьшего значения, т.е. существуют точки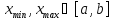такие, что

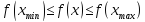
для любого .

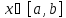Доказательство. Пусть 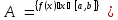. Если функция неограничена сверху, то полагаем здесьA=+∞ . Тогда найдется последовательность точек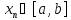таких, что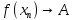. Выберем из нее сходящуюся подпоследовательность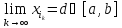(см. леммы выше). Тогда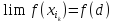в силу непрерывности. Тем самымA=f(d)<+∞ и ограниченность следует. Полагаем.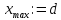

Аналогично доказывается существование.□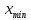

Для интервала аналогичное утверждение неверно -- см. пример неограниченной функции tgxна интервале (-π /2,π /2).

Теорема Больцано-Коши.Пусть функция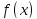непрерывна на отрезке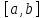и в концах отрезка принимает значения разных знаков. Тогда найдется точкатакая, чтоf(c)=0.

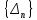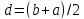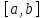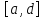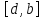Доказательство. Строим систему вложенных друг в друга отрезков . Первый из них -- отрезок. Далее рассмотрим точку-- середину отрезка. Еслиf(d)=0, тоc=d-- искомая точка. Иначе из двух отрезковивыбираем тот на концах которого функцияпринимает значения разных знаков. Его объявляеми с ним поступаем точно также как и с отрезком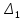(см. рис. 2).

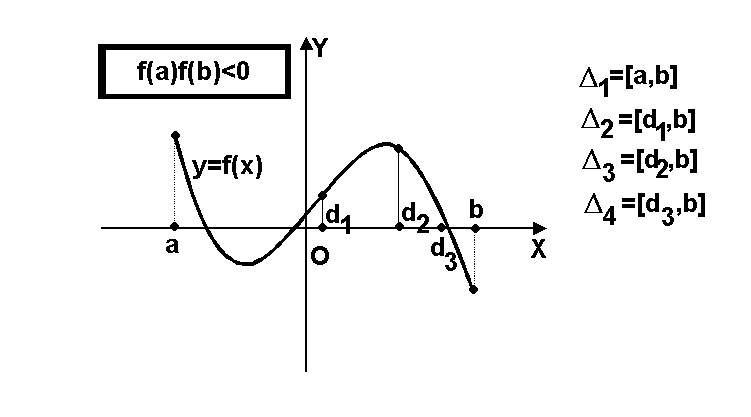
Рисунок 1. Решение уравнения f(x)=0 методом дихотомии

Либо мы на каком-то шаге придем к искомой точке c, либо получим бесконечную последовательность вложенных друг в друга отрезков

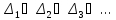
каждый последующий из которых вдвое короче предыдущего. Из принципа Кантора вложенных отрезков вытекает, что существует точка 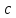принадлежащая всем отрезкам. Если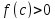, то найдется окрестность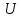точкиcтакая, чтодля любогоследует неравенство(устойчивость знака непрерывной функции). Но ясно, что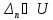для какого либоn. Это противоречит тому, что на концах отрезка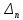функцияпринимает значения разных знаков. Аналогично приводится к противоречию предположение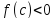. Остается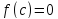, что и требовалось доказать.□

Следствие. Пусть функция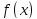непрерывна на отрезке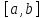. Обозначим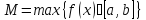,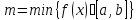. Тогда для любого числаCлежащего междуmиMнайдется точка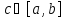такая, что.

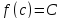Достаточно применить теорему Больцано-Коши к разности 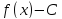и отрезкувместо.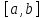

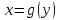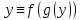Напомним, что функция называется обратной к функции, еслии.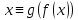

Например, 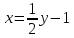обратна к функции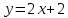. Немного не строго, в ситуации предыдущего определения, функцию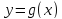также называют обратной к функции.

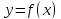Теорема [непрерывность обратной функции]. Еслинепрерывно и строго монотонно отображает отрезок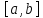в отрезок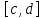так, чт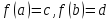о(либо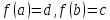в случае убывающей функции), то обратная функциясуществует, и она непрерывно и монотонно отображает отрезок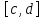на отрезок.

Доказательство. Существование обратной функции, т.е. фактически свойство 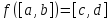, вытекает из следствия теоремы Больцано-Коши. Монотонностьgясна.

Пустьи𝜺>0. Предполагаем, что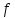возрастает. Тогда

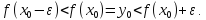
Возьмем

.

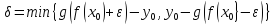Тогда для 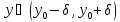выполняется неравенство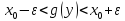. Это влечет непрерывность функцииg.□

Ранее мы уже определили корень арифметический n-ой степени из неотрицательного числа. Однако непрерывность корня мы можем обосновать только сейчас.

Следствие.Существует и единственен арифметический корень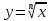-- непрерывная функция как обратная к непрерывной монотонной функции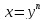.