
LEKTsII / Тема 9 Аналит_Геометрия
.docxАналитическая геометрия
Оглавление
1Прямая на плоскости 1
1.1Деление отрезка в заданном отношении 2
1.2Взаимное расположение двух прямых на плоскости. 3
2Плоскость в пространстве 5
3Прямая в пространстве 6
4Кривые второго порядка 8
1Эллипс 8
2Гипербола 9
3Парабола 10
-
Прямая на плоскости
Пусть
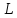 - прямая на плоскости,
- прямая на плоскости,
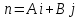 -- ненулевой вектор, перпендикулярный
-- ненулевой вектор, перпендикулярный
 ,
,
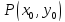 - какая-либо точка на прямой
- какая-либо точка на прямой
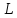 .
Тогда точка
.
Тогда точка
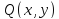 принадлежит прямой
принадлежит прямой
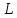 тогда и только тогда, когда вектор
тогда и только тогда, когда вектор
 перпендикулярен вектору
перпендикулярен вектору
 ,
а это имеет место в том и только том
случае, когда
,
а это имеет место в том и только том
случае, когда
 и это эквивалентно тому, что
и это эквивалентно тому, что
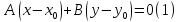
Итак, (1) --
уравнение прямой L, проходящей через
заданную точку
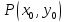 и перпендикулярную заданному вектору
и перпендикулярную заданному вектору
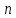 .
Отсюда, обозначив
.
Отсюда, обозначив
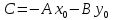 ,
получим:
,
получим:

-- общее уравнение прямой на плоскости. Далее:
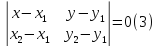
-- уравнение
прямой, проходящей через две не совпадающие
точки
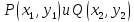 .
Действительно, подставляя в (3) вместо
.
Действительно, подставляя в (3) вместо
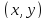 координаты заданных точек, получаем
верные равенства. Так как либо
координаты заданных точек, получаем
верные равенства. Так как либо
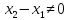 ,
либо
,
либо
 ,
то (3) действительно будет уравнением
прямой. Заметим, что вектор
,
то (3) действительно будет уравнением
прямой. Заметим, что вектор
 коллинеарен прямой
коллинеарен прямой
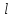 .
Соотношение (3) эквивалентно пропорции
.
Соотношение (3) эквивалентно пропорции
 ,
отсюда получаем решение еще одной
стандарной задачи:
,
отсюда получаем решение еще одной
стандарной задачи:

-- уравнение
прямой, проходящей через точку
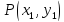 и коллинеарной заданному ненулевому
вектору
и коллинеарной заданному ненулевому
вектору
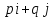 .
Если обе равные дроби в (4) считать
параметром
.
Если обе равные дроби в (4) считать
параметром
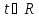 и выразить
и выразить
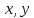 через этот параметр, то получим
через этот параметр, то получим

-- параметрическое уравнение прямой.
-
Деление отрезка в заданном отношении
Согласно
(5) и (4) параметрическое уравнение
прямой, проходящей через различные
точки
 и
и
 имеет вид
имеет вид
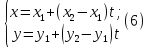
Значению
параметра
 соответствует точка P,
а значению
соответствует точка P,
а значению
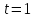 --- точка Q.
Отсюда следует, что точки отрезка PQ
описываются уравнениями с дополнительным
ограничением
--- точка Q.
Отсюда следует, что точки отрезка PQ
описываются уравнениями с дополнительным
ограничением
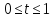 .
Поставим задачу: найти координаты точки
R, делящей отрезок PQ в отношении
.
Поставим задачу: найти координаты точки
R, делящей отрезок PQ в отношении
 (от точки P).
Здесь m,n
– неотрицательные числа, не равные 0
одновременно. Ответ таков:
(от точки P).
Здесь m,n
– неотрицательные числа, не равные 0
одновременно. Ответ таков:
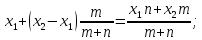

В частности
середина отрезка PQ имеет координаты
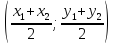 .
.
Пример.
Найдем уравнение срединного перпендикуляра
отрезка PQ. В качестве вектора n,
перпендикулярному этому срединному
перпендикуляру можно взять
 .
Получаем:
.
Получаем:
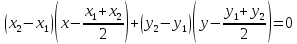
или

-
Взаимное расположение двух прямых на плоскости.
Пусть
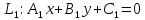 и
и
 - две прямые на плоскости. Тогда
- две прямые на плоскости. Тогда
а)
 пересекаются в точке тогда и только
тогда, когда
пересекаются в точке тогда и только
тогда, когда
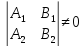
б)
 тогда и только тогда, когда
тогда и только тогда, когда
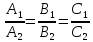 ;
;
в)
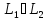 тогда и только тогда, когда
тогда и только тогда, когда
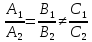 ;
;
г)
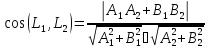 .
.
д)
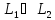 тогда и только тогда, когда
тогда и только тогда, когда
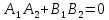 .
.
Утверждение а) следует из правила Крамара, примененного к системе

Расстояние
от точки
 до прямой L, заданной общим уравнением
(2), может быть вычислено по формуле:
до прямой L, заданной общим уравнением
(2), может быть вычислено по формуле:

Докажем
формулу (8) взяв на прямой L точку
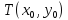 .
Вектор
.
Вектор
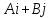 перпендикулярен L, а значит
вектор
перпендикулярен L, а значит
вектор
 коллинеарен L ,ибо скалярное
произведение этих двух векторов равно
0. Тогда и точка
коллинеарен L ,ибо скалярное
произведение этих двух векторов равно
0. Тогда и точка
 принадлежит прямой L.
Подсчитаем площадь параллелограмма,
построенного на векторах
принадлежит прямой L.
Подсчитаем площадь параллелограмма,
построенного на векторах
 и
и
 сначала как произведение основания
сначала как произведение основания
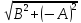 на высоту, а она равна
на высоту, а она равна
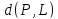 а затем как модуль векторного произведения
а затем как модуль векторного произведения
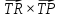 :
:
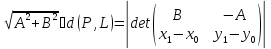
или
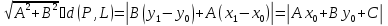
ибо
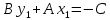 .
.
Полуплоскости,
определяемые прямой. Пусть на плоскости
задана прямая
 .
Прямая
.
Прямая
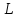 разделяет плоскость на две полуплоскости
разделяет плоскость на две полуплоскости
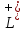 и
и
 ,
задаваемые неравенствами
,
задаваемые неравенствами
 и
и
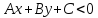 .
Если точки
.
Если точки
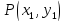 и
и
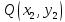 принадлежат одной полуплоскости, то и
весь отрезок
принадлежат одной полуплоскости, то и
весь отрезок
 принадлежит этой полуплоскости. Если
же точки
принадлежит этой полуплоскости. Если
же точки
 и
и
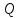 принадлежат разным полуплоскостям, то
любая непрерывная кривая, соединяющая
принадлежат разным полуплоскостям, то
любая непрерывная кривая, соединяющая
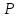 с
с
 пересекает прямую
пересекает прямую
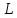 ,
а отрезок PQ пересекает L ровно в одной
точке.
,
а отрезок PQ пересекает L ровно в одной
точке.
-
Плоскость в пространстве
Пусть π -
плоскость в пространстве,
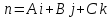 -- ненулевой вектор, перпендикулярный
плоскости
-- ненулевой вектор, перпендикулярный
плоскости
 ,
,
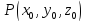 - какая-либо точка на плоскости π . Тогда
- какая-либо точка на плоскости π . Тогда
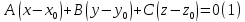
-- уравнение
плоскости π , проходящей через заданную
точку
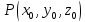 и перпендикулярную заданному вектору
n. Отсюда:
и перпендикулярную заданному вектору
n. Отсюда:

-- общее уравнение плоскости в пространстве. Далее:

-- уравнение
плоскости, проходящей через три точки
 ,
,
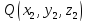 ,
,
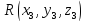 ,
не лежащие на одной плоскости.
,
не лежащие на одной плоскости.

-- уравнение
плоскости, проходящей через точку
 и коллинеарной двум векторам
и коллинеарной двум векторам
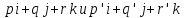 ,
не коллинеарным между собой.
,
не коллинеарным между собой.
Взаимное
расположение двух плоскостей в
пространстве. Пусть
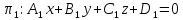 и
и
 - две плоскости в пространстве. Тогда:
- две плоскости в пространстве. Тогда:
а)
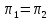 тогда и только тогда, когда
тогда и только тогда, когда
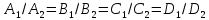 ;
;
б)
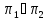 тогда и только тогда, когда
тогда и только тогда, когда
 ;
;
в)

г)
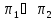 тогда и только тогда, когда
тогда и только тогда, когда
 ;
;
Расстояние
от точки
 до плоскости π может быть вычислено по
формуле:
до плоскости π может быть вычислено по
формуле:

Полупространства,
определяемые плоскостью. Пусть в
пространстве задана плоскость
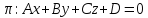 .
Плоскость π разделяет пространство
на два полупространства, задаваемые
неравенствами Ax+By+Cz+D>0 и Ax+By+Cz+D<0. Если
точки
.
Плоскость π разделяет пространство
на два полупространства, задаваемые
неравенствами Ax+By+Cz+D>0 и Ax+By+Cz+D<0. Если
точки
 и
и
 принадлежат
одному полупространству, то и весь
отрезок
принадлежат
одному полупространству, то и весь
отрезок
 принадлежит этому же полупространству.
Если же точки
принадлежит этому же полупространству.
Если же точки
 и
и
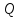 принадлежат разным полупространствам,
то любая непрерывная кривая, соединяющая
принадлежат разным полупространствам,
то любая непрерывная кривая, соединяющая
 с
с
 пересекает плоскость
пересекает плоскость
 .
.
-
Прямая в пространстве
Пусть
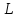 - прямая в пространстве,
- прямая в пространстве,
 и ненулевой вектор
и ненулевой вектор
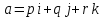 коллинеарен прямой
коллинеарен прямой
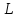 .
Тогда
.
Тогда
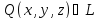 тогда и только тогда, когда вектор
тогда и только тогда, когда вектор
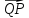 коллинеарен вектору
коллинеарен вектору
 ,
а это имеет место в том и только том
случае, когда
,
а это имеет место в том и только том
случае, когда
 для некоторого t∈
ℝ . Переходя к
покоординатной записи, получаем
для некоторого t∈
ℝ . Переходя к
покоординатной записи, получаем
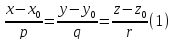
-- каноническое уравнение прямой в пространстве, а

-- параметрическое уравнение прямой в пространстве.
Общее уравнение прямой в пространстве имеет вид:
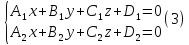
где вектора
 не
коллинеарны.
не
коллинеарны.
Расположение двух прямых в пространстве. Пусть в пространстве заданы две прямые - L, уравнением (1), и

Тогда:
а) L=L' тогда и только тогда, когда
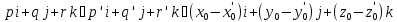 ;
;
б) L∥ L' тогда и только тогда, когда
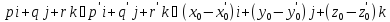 ;
;
в)
 ;
;
г) L и L' лежат в одной плоскости тогда и только тогда, когда

д) L и L' скрещиваются тогда и только тогда, когда определитель в (3) не равен нулю
-
Кривые второго порядка
-
Эллипс
-
Эллипс это
геометрическое место точек на плоскости,
сумма расстояний которых до двух
фиксированных точек есть величина
постоянная. Две точки, о которых идёт
речь в определении эллипса, называются
фокусами эллипса, расстояние между ними
называется фокальным расстоянием.
Обозначим половину фокального расстояния
через
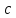 ,
а половину суммы от точки на эллипсе до
фокусов обозначим
,
а половину суммы от точки на эллипсе до
фокусов обозначим
 .
Эта величина называется большой
полуосью. Заметим, что случай c=0 не
исключается, он приводит к окружности
радиуса
.
Эта величина называется большой
полуосью. Заметим, что случай c=0 не
исключается, он приводит к окружности
радиуса
 .
Выберем систему координат на плоскости
так, что точки
.
Выберем систему координат на плоскости
так, что точки
 -- фокусы эллипса. Обозначим также
-- фокусы эллипса. Обозначим также
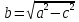 ;
-- малая полуось. Очевидно, что
;
-- малая полуось. Очевидно, что
 .
Тогда каноническое уравнение эллипса
будет следующее
.
Тогда каноническое уравнение эллипса
будет следующее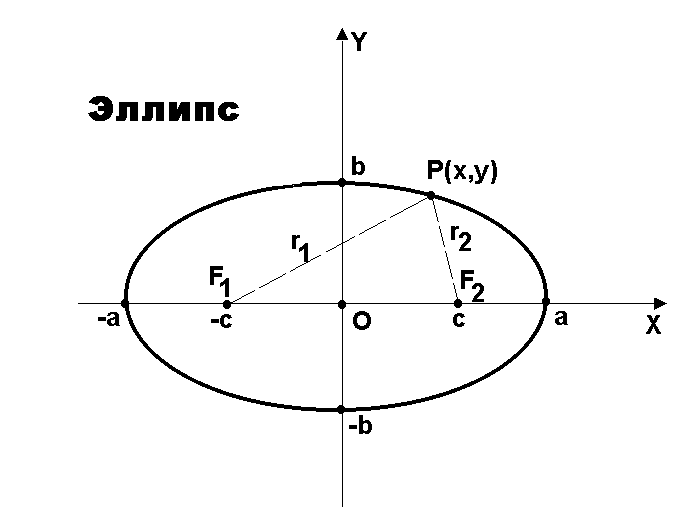
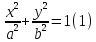
Величину
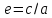 называют эксцентриситетом. Ясно, что
0≤ e<1 для эллипса, и чем ближе e к 1 тем
более сплюснут эллипс. Более точно,
эллипс (1) получается из окружности
называют эксцентриситетом. Ясно, что
0≤ e<1 для эллипса, и чем ближе e к 1 тем
более сплюснут эллипс. Более точно,
эллипс (1) получается из окружности
 сжатием по оси OY в
сжатием по оси OY в

 раз,
т.е. если точка
раз,
т.е. если точка
 лежит на окружности
лежит на окружности
 ,
то точка
,
то точка
 ,
где
,
где
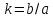 лежит на эллипсе (1). Отсюда, в частности,
следует, что площадь эллипса равна
лежит на эллипсе (1). Отсюда, в частности,
следует, что площадь эллипса равна
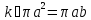 .
Точки
.
Точки
 называются вершинами эллипса. Эллипс
(1) симметричен относительно оси
называются вершинами эллипса. Эллипс
(1) симметричен относительно оси
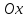 ,
называемой большой или фокальной ось,
а также симметричен относительно оси
,
называемой большой или фокальной ось,
а также симметричен относительно оси
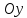 (малая ось).
(малая ось).
Пусть
 -- точка на эллипсе. Расстояния
-- точка на эллипсе. Расстояния
 называются фокальными. Можно доказать,
что
называются фокальными. Можно доказать,
что
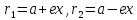 .
.
-
Гипербола
Гипербола
есть геометрическое место точек на
плоскости, модуль разность расстояний
которых до двух фиксированных точек,
называемых фокусами гиперболы, есть
величина постоянная, обозначаемая, как
и выше, через
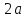 .
Так же как для эллипса, обозначим через
c -- половину фокального расстояния. Но
для гиперболы
.
Так же как для эллипса, обозначим через
c -- половину фокального расстояния. Но
для гиперболы
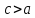 ;
поэтому определена величина
;
поэтому определена величина
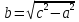 .
Расположим фокусы гиперболы
.
Расположим фокусы гиперболы
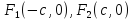 также как и для эллипса. Тогда каноническое
уравнение гиперболы будет такое:
также как и для эллипса. Тогда каноническое
уравнение гиперболы будет такое:

Эксцентриситет
для гиперболы определяется также как
и для эллипса:
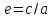 ,
но он уже больше 1 и чем ближе к 1, тем
более сплюснута гипербола. Гипербола,
в отличии от эллипса, неограниченная
линия на плоскости. Она имеет пару
асимптот:
,
но он уже больше 1 и чем ближе к 1, тем
более сплюснута гипербола. Гипербола,
в отличии от эллипса, неограниченная
линия на плоскости. Она имеет пару
асимптот: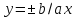 .
Координатные оси являются осями симметрии
гиперболы. Если
.
Координатные оси являются осями симметрии
гиперболы. Если
 ,
то гипербола называется равнобочной.
В координатах,
,
то гипербола называется равнобочной.
В координатах,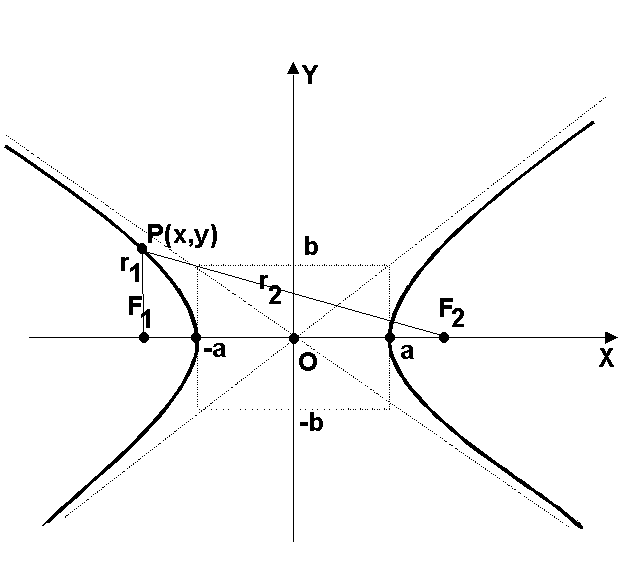
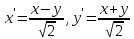
повернутых
относительно канонических координат
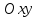 (см. (1)) на
(см. (1)) на
 ,
уравнение равнобочной гиперболы
приобретает вид
,
уравнение равнобочной гиперболы
приобретает вид
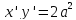 или
или
 -- известная из школы функциональная
обратно пропорциональная зависимость.
Мы видим, что гипербола имеет две ветви
-- левую и правую.
-- известная из школы функциональная
обратно пропорциональная зависимость.
Мы видим, что гипербола имеет две ветви
-- левую и правую.
Пусть
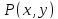 -- точка на гиперболе. Расстояния
-- точка на гиперболе. Расстояния
 называются фокальными. Можно доказать,
что
называются фокальными. Можно доказать,
что
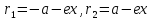 при
при
 и
и
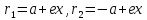 при
при
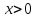 .
.
-
Парабола
Парабола
-- геометрическое место точек на плоскости,
расстояния которых до фиксированной
точки (фокус параболы) и до фиксированной
прямой (директрисса параболы) равны.
Если обозначить расстояние от фокуса
до директриссы через p, (p>0 по определению),
поместить фокус в точку
 а директрису отождествить с прямой
x=-p/2, то каноническое уравнение параболы
будет выглядеть так:
а директрису отождествить с прямой
x=-p/2, то каноническое уравнение параболы
будет выглядеть так:
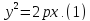
Действительно,
точка
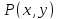 принадлежит параболе в точности тогда,
когда
принадлежит параболе в точности тогда,
когда


Парабола (1) имеет ось OX своей осью симметрии. Точка O(0,0) - начало координат, будет левой крайней точкой параболы (1). Она называется вершиной параболы. У параболы также есть эксцентриситет, он равен 1 и не зависит от p.
