
- •Оглавление
- •Системы линейных уравнений с одним идвумя неизвестными
- •Системы с тремя неизвестными
- •Метод Гаусса решения систем линейных уравнений.
- •Исследование системы по ступенчатому виду.
- •Матричное исчисление
- •Произведение матриц
- •Подстановки
- •Определители
- •Вычисление определителей некоторых матриц
- •Правило Крамара
- •Обратная матрица
Системы. Матрицы. Определители
Оглавление
1Системы линейных уравнений с одним идвумя неизвестными 1
2Системы с тремя неизвестными 6
3Метод Гаусса решения систем линейных уравнений. 6
3.1Исследование системы по ступенчатому виду. 9
4Матричное исчисление 11
4.1Произведение матриц 12
5Подстановки 13
6Определители 14
7Вычисление определителей некоторых матриц 18
8Правило Крамара 19
9Обратная матрица 21
Системы линейных уравнений с одним идвумя неизвестными
Общий
вид линейного уравнения с одним
неизвестным
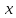 следующий:
следующий:
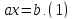
Здесь
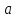 и
и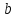 какие-то действительные числа. Мы ищем
все решения уравнения (1), т.е. такие
числа, при подстановке которых вместо
какие-то действительные числа. Мы ищем
все решения уравнения (1), т.е. такие
числа, при подстановке которых вместо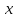 ,
получается слева в (1) то же число, что и
справа. Сформулируем ответ.
,
получается слева в (1) то же число, что и
справа. Сформулируем ответ.
Случай
1:
 Тогда
решение единственно и равно
Тогда
решение единственно и равно .
.
Случай
2:
 ,
но
,
но .
Тогда решений нет или, по-другому,
множество решений пусто.
.
Тогда решений нет или, по-другому,
множество решений пусто.
Случай
3:
 .
Тогда множество решений -- вся числовая
ось, т.е. все множество действительных
чиселℝ.
.
Тогда множество решений -- вся числовая
ось, т.е. все множество действительных
чиселℝ.
Перейдем к одному уравнению с двумя неизвестными

Случай
1:
 .
Тогда уравнение (2) эквивалентно
функциональной зависимости
.
Тогда уравнение (2) эквивалентно
функциональной зависимости ,
графиком которой служит наклонная
прямая на плоскости.
,
графиком которой служит наклонная
прямая на плоскости.
Случай
2:
 ,
но
,
но .
Тогда уравнение (2) эквивалентно
.
Тогда уравнение (2) эквивалентно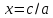 .
Множество точек на плоскости,
удовлетворяющих этому соотношению есть
вертикальная прямая.
.
Множество точек на плоскости,
удовлетворяющих этому соотношению есть
вертикальная прямая.
Случай
3:
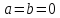 ,
но
,
но .
Тогда решений нет.
.
Тогда решений нет.
Случай
4:
 .
Тогда все пары чисел являются решениями.
.
Тогда все пары чисел являются решениями.
Перейдем
теперь к линейной системе 2×2 с неизвестными
 и
и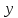 .
Общий вид её следующий:
.
Общий вид её следующий:

Фигурная скобка слева в (3) заменяет союз
"и". Нам надо найти все пары чисел
 ,
при подстановке которых в первоеиво второе уравнение системы (3) получаются
верные числовые равенства. Исключим
неизвестное
,
при подстановке которых в первоеиво второе уравнение системы (3) получаются
верные числовые равенства. Исключим
неизвестное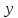 из системы (3). Для этого первое уравнение
умножим на
из системы (3). Для этого первое уравнение
умножим на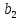 ,
второе -- на
,
второе -- на ,
и вычтем из полученного первого уравнения
получившееся второе уравнение. Далее
исключим неизвестное
,
и вычтем из полученного первого уравнения
получившееся второе уравнение. Далее
исключим неизвестное из системы (3), для чего первое уравнение
умножим на
из системы (3), для чего первое уравнение
умножим на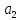 ,
второе -- на
,
второе -- на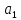 ,
и вычтем из полученного второго уравнения
первое. Получим следующую систему:
,
и вычтем из полученного второго уравнения
первое. Получим следующую систему:
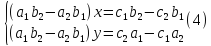
Система
двух уравнений (4) является следствием
системы (3). Это значит, что равенства
(4) верны, коль скоро пара
 есть решение системы (3). Если внимательно
присмотреться к коэффициентам системы
(4), то можно заметить, что все они
составлены по одному и тому же правилу.
Назовём следующую конструкцию
есть решение системы (3). Если внимательно
присмотреться к коэффициентам системы
(4), то можно заметить, что все они
составлены по одному и тому же правилу.
Назовём следующую конструкцию
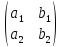
2×2-матрицей
с коэффициентами
 ,
а число
,
а число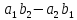 назовем ее определителем и будем
записывать так:
назовем ее определителем и будем
записывать так:
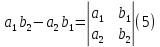
Определитель (5) также называют определителем системы (3). Будем обозначать этот определитель прописной греческой буквой Δ ("дельта"). Правые части уравнений (4) также являются определителями, но уже других матриц. Обозначим их следующим образом:
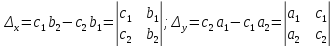
Итак, следствием системы (3) является "распадающаяся" или диагональная система

которую мы уже знаем как решать.
Случай
1:
 .
Тогда система (4) имеет единственное
решение
.
Тогда система (4) имеет единственное
решение
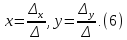
Оказывается,
что (6) в случае
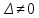 есть единственное решение системы (3).
Эта формулировка правила Крамара для
системы 2× 2. Мы сформулировали правило
Крамара, но доказали лишь единственность
решения (6), а сам факт, что (6) есть решение
системы (3) установить можно прямой
проверкой:
есть единственное решение системы (3).
Эта формулировка правила Крамара для
системы 2× 2. Мы сформулировали правило
Крамара, но доказали лишь единственность
решения (6), а сам факт, что (6) есть решение
системы (3) установить можно прямой
проверкой:

Аналогично
проверяется, что пара чисел
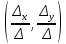 является решением и второго уравнения
системы (3).
является решением и второго уравнения
системы (3).
Случай
2:
 ,
но либо
,
но либо ,
либо
,
либо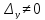 .
Тогда одно из уравнений системы (4) не
имеет решения. Отсюда немедленно
вытекает, что система (3) не имеет решений,
так как (4) есть следствие системы (3).
.
Тогда одно из уравнений системы (4) не
имеет решения. Отсюда немедленно
вытекает, что система (3) не имеет решений,
так как (4) есть следствие системы (3).
Случай
3:
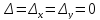 .
Конечно, в этом случае система (4) имеют
решениями все пары чисел. Но это не
значит, что любая пара чисел является
решением исходной системы (3). Например,
в системе
.
Конечно, в этом случае система (4) имеют
решениями все пары чисел. Но это не
значит, что любая пара чисел является
решением исходной системы (3). Например,
в системе все
определители
все
определители равны нулю, но решением ее будет
биссектриса второго и четвертого
квадрантов.
равны нулю, но решением ее будет
биссектриса второго и четвертого
квадрантов.
Если
 ,
то второму уравнению удовлетворяет
любая пара чисел, так что его без ущерба
для множества решений можно выбросить
из системы. Но тогда мы возвращаемся в
уже исследованный случай одного уравнения
с двумя неизвестными.
,
то второму уравнению удовлетворяет
любая пара чисел, так что его без ущерба
для множества решений можно выбросить
из системы. Но тогда мы возвращаемся в
уже исследованный случай одного уравнения
с двумя неизвестными.
Считаем
теперь, что тройка
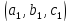 ненулевая, т.е. по крайней мере, одна из
компонент этой тройки есть ненулевое
число. Тогда равенства
ненулевая, т.е. по крайней мере, одна из
компонент этой тройки есть ненулевое
число. Тогда равенства можно переписать как пропорции:
можно переписать как пропорции:
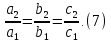
Не
следует смущаться, если в знаменателе
пропорции окажется ноль. По определению
пропорция
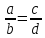 имеет место, если накрест лежащие
произведения равны:
имеет место, если накрест лежащие
произведения равны: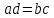 .
Обозначим общее отношение (7) греческой
буквой("лямбда").
Тогда тройка коэффициентов
.
Обозначим общее отношение (7) греческой
буквой("лямбда").
Тогда тройка коэффициентов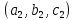 получается из тройки
получается из тройки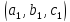 умножением нав
том смысле, что
умножением нав
том смысле, что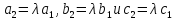 .
А это означает, в свою очередь, что если
мы ко второму уравнению системы (3)
прибавим первое уравнение, предварительно
умноженное на, то
придем к системе вида
.
А это означает, в свою очередь, что если
мы ко второму уравнению системы (3)
прибавим первое уравнение, предварительно
умноженное на, то
придем к системе вида

Система
(3) в свою очередь может быть получена
из системы (8) обратным преобразованием:
надо ко второму уравнению системы (8)
прибавить первое, умноженное на 1/. (Если бы было=0,
то и мы бы начинали с отбрасывания первого
уравнения). Это значит, что системы (3)
и (8) имеют одно и то же множество решений,
или как мы будем говорить, они эквивалентны.
Понятно, что система (8) проще устроена,
чем (3), и мы будем решать именно ее. Как
уже отмечалось, нулевое уравнение можно
отбросить, и мы снова возвращаемся к
случаю одного уравнения с двумя
неизвестными.
и мы бы начинали с отбрасывания первого
уравнения). Это значит, что системы (3)
и (8) имеют одно и то же множество решений,
или как мы будем говорить, они эквивалентны.
Понятно, что система (8) проще устроена,
чем (3), и мы будем решать именно ее. Как
уже отмечалось, нулевое уравнение можно
отбросить, и мы снова возвращаемся к
случаю одного уравнения с двумя
неизвестными.
Мы
полностью решили систему 2×2. Подведем
итог. В случае отличия от нуля определителя
системы, решение единственно. Если же
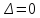 ,
то решений может не быть вовсе, либо
может быть бесконечное множество
решений, образующих прямую на декартовой
плоскости
,
то решений может не быть вовсе, либо
может быть бесконечное множество
решений, образующих прямую на декартовой
плоскости .
В случае равенства нулю всех коэффициентов,
множество решений заполняет всю плоскость
.
В случае равенства нулю всех коэффициентов,
множество решений заполняет всю плоскость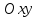 .
.
Мы
не случайно в последнем абзаце прибегнули
к геометрии. Если есть возможность
какой-либо математический объект
истолковать геометрически, то этой
возможностью надо обязательно
воспользоваться. То, что такая возможность
есть для системы 2×2, показывает следующая
таблица (в этой таблице предполагается,
что пары коэффициента
 и
и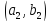 ненулевые.
ненулевые.
|
Аналитический язык
|
Геометрический язык |
|
Пара чисел
|
Точка
|
|
Уравнение
|
Прямая на плоскости
|
|
Решение системы (3) |
Поиск пересечения двух прямых –
|
|
Решение системы (3) единственно
( |
Прямые
|
|
Система (3) решений не имеет |
Прямые
|
|
Система (3) имеет бесконечное множество решений |
Прямые
|

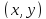
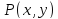 на плоскости
на плоскости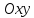
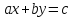 (
(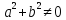 )
)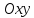
 и
и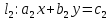
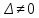 )
) и
и пересекаются
пересекаются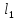 и
и параллельны
параллельны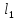 и
и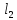 совпадают.
совпадают.