7. Вычисление определителей некоторых матриц

Определитель с углом нулей.Пусть A,B -- квадратные матрицы (не обязательно одинакового размера). Тогда

для любой матрицы C подходящего размера. Аналогично,

для любой матрицы D подходящего размера.

Теорема.Определитель произведения матриц равен произведению определителей:(для любых-матрици).

Доказательство. Применим предыдущую теорему и свойства определителей:

□

Квадратная матрица A называется невырожденной, если , и называется вырожденной в противном случае.

Следствие.Произведение вырожденной матрицы на любую квадратную матрицу того же размера снова будет вырожденной матрицей. Произведение невырожденных матриц является невырожденной матрицей.

Теорема 6 (Определитель Вандермонда). Для любыхимеет место равенство:

В правой части здесь стоит произведение вида

(всего n(n-1)/2 сомножителей.)

Доказательство. Начиная справа, вычтем из каждого последующего столбца предыдущий, умноженный на , а далее разложим по получившейся первой строке -- (1,0,0,… ,0) . Приходим к определителю (n-1)×(n-1) :

Далее вынесем из строк множители и сведем задачу к вычислению такого же определителя меньшего размера. Применение индукции заканчивает доказательство.□

8. Правило Крамара

Рассмотрим линейную систему n уравнений с n неизвестными:

Правило Крамара.Система (1) определена тогда и только тогда, когда матрица A невырождена. В этом случае решение находится по формулам:

где - матрица, полученная из матрицы A заменой i –го столбца на столбец свободных членов.

Доказательство. Заметим, что при элементарных преобразованиях системы 1-3 типов свойство невырожденности (вырожденности) матрицы системы сохраняется. Следовательно, если , то в ступенчатом виде на главной диагонали должны стоять ненулевые элементы (см. теорему об определителе треугольной матрицы), т. е. система (1) будет определенной. Наоборот, если система (1) определена, то все неизвестные -- главные, следовательно матрица ступенчатого вида невырождена, и поэтому. Остается проверить формулу (1) в случае.

Фиксируем натуральное число . Умножим i -ое уравнение системы (1) на-- алгебраическое дополнение элементаматрицы A , и результаты просуммируем по i=1,2,… ,n . Тогда в силу свойства "ложного разложения" по столбцу матрицы A будем иметьдля всякого j≠ k , а. Тем самым результат после суммирования будет следующий:

(Последнее равенство верно в силу разложения по k -ому столбцу). Отсюда находими тем самым доказательство правила Крамара завершено.□

Следствие доказательства.Если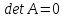, нодля какого-либо k , то система (1) несовместна.

Теорема. Пусть (1) -- однородная система, т. е.. Эта система имеет ненулевое решение тогда и только тогда, когда.

Доказательство. Так как однородная система всегда совместна, то остается две возможности - эта система либо определена (т. е. имеет только нулевое решение), либо неопределена (т. е. имеет ненулевое решение). Остается применить правило Крамара. □

9. Обратная матрица

Матрица Dназывается обратной кn×n-матрице А, еслиAD=DA=E. Обратная матрица, если оно существует, единственна (см. единственность обратного элемента в полеℝ)

Теорема 1. Обратная матрица к n×n -матрице A существует тогда и только тогда, когда матрица A невырождена. В этом случае

где , как и ранее, алгебраическое дополнение к (i,j) -тому элементу матрицы.A.

Доказательство. Если матрица A вырождена, то и AB вырождена, поэтому произведение не может быть равно единичной матрице.

Предположим теперь, что . Тогда правая часть в (1) определена и можно убедиться непосредственной проверкой, что ее произведение на матрицу A дает единичную матрицу; при этом используются свойства разложения и ложного разложения определителя матрицы по столбцу (строке).□

Предложение 1.Имеет место равенстводля любой невырожденной матрицы A .

21