
LEKTsII / Тема 6 Исследование функций
.docxИсследование функций
Оглавление
Экстремумы. Монотонность. 1
Выпуклость и вогнутость 3
Асимптоты 5
Экстремумы. Монотонность.
Определение.
Функция
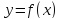 называется возрастающей (убывающей)
на множестве
называется возрастающей (убывающей)
на множестве
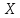 ,
если для любых
,
если для любых
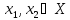 таких, что
таких, что
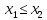 следует
неравенство
следует
неравенство
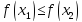 (
(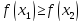 ).
Возрастающая или убывающая функция
называется монотонной. Функция
).
Возрастающая или убывающая функция
называется монотонной. Функция
 называется строго возрастающей
(строго убывающей) на множестве
называется строго возрастающей
(строго убывающей) на множестве
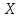 ,
если для любых
,
если для любых
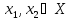 таких, что
таких, что
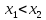 следует
неравенство
следует
неравенство
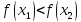 (
(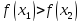 ).
Строго возрастающая или строго убывающая
функция называется строго монотонной.
).
Строго возрастающая или строго убывающая
функция называется строго монотонной.
Теорема.
Пусть
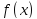 дифференцируема на интервале
дифференцируема на интервале
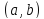 ,
и
,
и
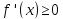 (
(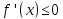 )
для любой точки
)
для любой точки
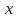 этого интервала. Тогда
этого интервала. Тогда
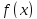 возрастает (убывает) на
возрастает (убывает) на
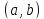 .
Верно и обратное утверждение.
.
Верно и обратное утверждение.
Доказательство.
Если
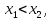 то по теореме Лагранжа найдется точка
то по теореме Лагранжа найдется точка
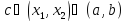 такая, что
такая, что
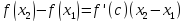 .
В силу того, что
.
В силу того, что
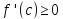 и
и
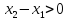 имеем:
имеем:
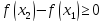 ,
т.е.
,
т.е.
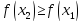 .
□
.
□
Точка
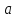 называется критической точкой функции
называется критической точкой функции
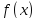 ,
если производная
,
если производная
 существует и равна 0. Необходимое условие
экстремума может быть сформулировано
так: для дифференцируемой функции любая
точка локального экстремума является
критической. Обратное утверждение
неверно как показывает пример кубической
параболы
существует и равна 0. Необходимое условие
экстремума может быть сформулировано
так: для дифференцируемой функции любая
точка локального экстремума является
критической. Обратное утверждение
неверно как показывает пример кубической
параболы
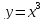 ,
которая в нуле имеет нулевую производную,
т.е. 0 - критическая точка, но эта точка
не является экстремальной.
,
которая в нуле имеет нулевую производную,
т.е. 0 - критическая точка, но эта точка
не является экстремальной.
Первое
достаточное условие экстремума. Пусть
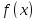 дифференцируема в окрестности точки
дифференцируема в окрестности точки
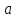 ,
и производная
,
и производная
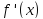 при переходе через точку a меняет знак.
Тогда
при переходе через точку a меняет знак.
Тогда
 -- точка экстремума. При этом
-- точка экстремума. При этом
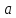 -- локальный максимум, если смена знака
производной происходит с плюса на минус,
и
-- локальный максимум, если смена знака
производной происходит с плюса на минус,
и
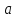 -- локальный минимум, если знак меняется
с минуса на плюс.
-- локальный минимум, если знак меняется
с минуса на плюс.
Доказательство -- следствие теоремы. □
Второе
достаточное условие экстремума. Пусть
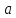 -- критическая точка дважды непрерывно
дифференцируемой функции
-- критическая точка дважды непрерывно
дифференцируемой функции
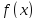 .
Если
.
Если
 ,
то
,
то
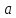 -- локальный минимум. Если же
-- локальный минимум. Если же
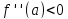 ,
то
,
то
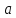 -- локальный максимум.
-- локальный максимум.
Доказательство.
Если
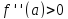 ,
то
,
то
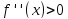 в некоторой достаточно малой окрестности
точки
в некоторой достаточно малой окрестности
точки
 (пользуемся непрерывностью второй
производной). Тогда по теореме производная
(пользуемся непрерывностью второй
производной). Тогда по теореме производная
 возрастает в этой окрестности. С учетом
равенства
возрастает в этой окрестности. С учетом
равенства
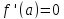 это влечет, в частности, то, что
это влечет, в частности, то, что
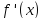 меняет знак с минуса на плюс при переходе
через точку
меняет знак с минуса на плюс при переходе
через точку
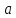 .
Первое достаточное условие экстремума
тогда утверждает, что
.
Первое достаточное условие экстремума
тогда утверждает, что
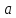 -- локальный минимум. Второй случай
разбирается аналогично. □
-- локальный минимум. Второй случай
разбирается аналогично. □
Пусть
функция
 непрерывна на отрезке
непрерывна на отрезке
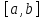 и дифференцируема на интервале
и дифференцируема на интервале
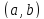 .
Поставим задачу о вычислении наибольшего
и наименьшего значения функции
.
Поставим задачу о вычислении наибольшего
и наименьшего значения функции
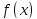 на отрезке
на отрезке
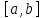 .
Напомним, что они существуют согласно
теореме Вейерштрасса.
.
Напомним, что они существуют согласно
теореме Вейерштрасса.
Теорема.
Пусть
 -- все критические точки функции
-- все критические точки функции
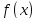 на интервале
на интервале
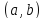 .
Тогда
.
Тогда
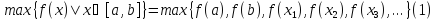
и

Доказательство.
Пусть в точке
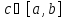 функция
функция
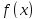 достигает наибольшего значения (см.
теорему Вейерштрасса). Если
достигает наибольшего значения (см.
теорему Вейерштрасса). Если
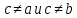 ,
т.е.
,
т.е.
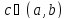 ,
то
,
то
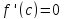 по теореме Ферма. Седовательно,
по теореме Ферма. Седовательно,
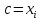 для какого-либо
для какого-либо
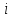 ,
и равенство (1) следует. Если же c
совпадает с одной из концевых точек
отрезка
,
и равенство (1) следует. Если же c
совпадает с одной из концевых точек
отрезка
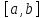 ,
то равенство (1) тривиально.
,
то равенство (1) тривиально.
Выпуклость и вогнутость
График
дифференцируемой на интервале
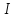 функции
функции
 называется выпуклым вверх или
просто выпуклым (выпуклым вниз или
вогнутым), если он лежит ниже (выше)
касательной, проведенной в любой точке
(см. рис ).
называется выпуклым вверх или
просто выпуклым (выпуклым вниз или
вогнутым), если он лежит ниже (выше)
касательной, проведенной в любой точке
(см. рис ).
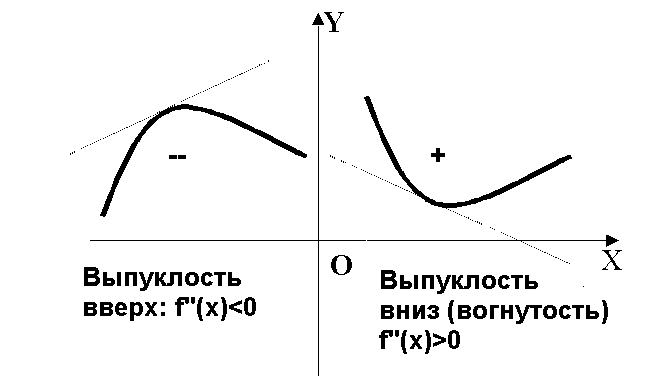
Рис. Выпуклость и вогнутость
Так
как уравнение касательной в точке
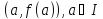 есть
есть
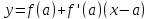 ,
то условие выпуклости будет таким:
,
то условие выпуклости будет таким:

Условие вогнутости будет следующим:
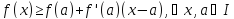
Достаточное
условие выпуклости. Пусть функция
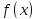 дважды дифференцируема на интервале
дважды дифференцируема на интервале
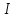 и
и
 для любой точки
для любой точки
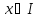 .
Тогда график этой функции вогнут на
интервале
.
Тогда график этой функции вогнут на
интервале
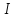 .
Если же
.
Если же
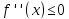 для любой
для любой
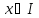 ,
то график функции
,
то график функции
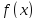 выпукл.
выпукл.
Доказательство.
Рассмотрим лишь случай
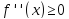 .
Докажем неравенство (2), убедившись, что
разность левой и правой части
неотрицательна:
.
Докажем неравенство (2), убедившись, что
разность левой и правой части
неотрицательна:
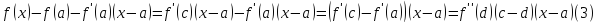
Точки
 и
и
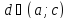 для которых верно (3) гайдутся согласно
теоремы Лагранжа. Если
для которых верно (3) гайдутся согласно
теоремы Лагранжа. Если
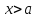 ,
то
,
то
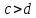 .
Если же
.
Если же
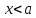 ,
то и
,
то и
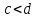 .
В любом случае
.
В любом случае
 .
Тогда и все произведение в правой части
(3) будет неотрицательным. □
.
Тогда и все произведение в правой части
(3) будет неотрицательным. □
Определение. Точка, при переходе через которую график функции меняет выпуклость, называется точкой перегиба.
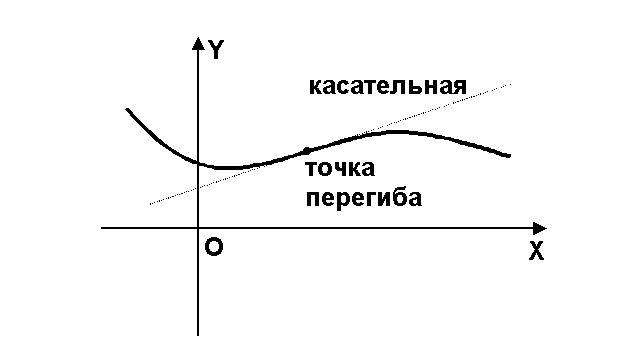
Рис. Точка перегиба
Другое
определение точки перегиба:
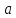 -- точка перегиба дифференцируемой
функции
-- точка перегиба дифференцируемой
функции
 ,
если график функции
,
если график функции
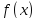 лежит по обе стороны от касательной
(или, иначе, переходит с одной стороны
касательной на другую), проведенной к
графику этой функции в точке
лежит по обе стороны от касательной
(или, иначе, переходит с одной стороны
касательной на другую), проведенной к
графику этой функции в точке
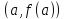 (см. рис.).
(см. рис.).
Асимптоты
Прямая ℓ называется асимптотой кривой γ , если ρ (P,ℓ )→ 0 при условии P→ ∞ , P∈ γ (см. рис. ).
Асимптоты
графика функции
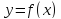 бывают вертикальные, т.е. задающиеся
уравнением
бывают вертикальные, т.е. задающиеся
уравнением
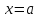 и наклонными, т.е. те прямые, которые
задаются уравнением
и наклонными, т.е. те прямые, которые
задаются уравнением
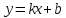 .
.
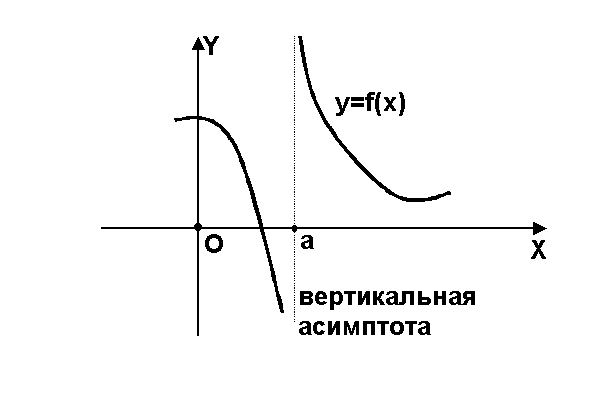
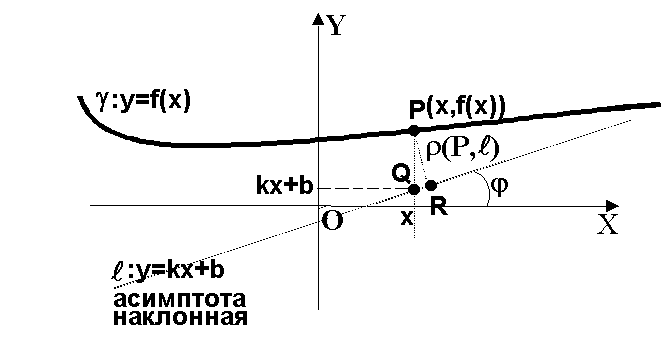
Рис. Асимптоты
Теорема.
Прямая
 является вертикальной асимптотой тогда
и только тогда, когда либо
является вертикальной асимптотой тогда
и только тогда, когда либо
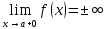 ,
либо
,
либо
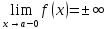 (см. рис. ).
(см. рис. ).
Прямая
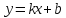 будет
наклонной асимптотой к графику функции
будет
наклонной асимптотой к графику функции
 на +∞ (на -∞ ), если и только если существуют
следующие пределы
на +∞ (на -∞ ), если и только если существуют
следующие пределы
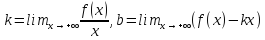
Доказательство.
Из
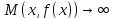 и
и
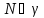 вытекает
вытекает
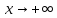 .
Тогда при x→ +∞ имеют
место эквивалентности:
.
Тогда при x→ +∞ имеют
место эквивалентности:
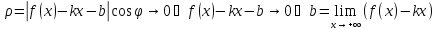
Отсюда следует
 для некоторой б.м. α (x).
Тогда
для некоторой б.м. α (x).
Тогда
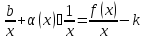
и
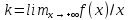 .
.
