
Функции
Оглавление
1Функции 1
1.1Декартовы координаты на плоскости 3
1.2Основные элементарные функции 4
1.3Линейные функции 6
1.4Модуль и знак 7
1.5Параболы. Гипербола. 8
1.6Показательные и логарифмические функции 8
1.7 Тригонометрические функции 12
Произведения 16
Степени 16
Суммы 17
Однопараметрическое представление 17
1.8Обратные тригонометрические функции 17
Функции
Пусть
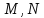 -- числовые множества.Функцией одной
переменнойс областью определения
(ОДЗ)
-- числовые множества.Функцией одной
переменнойс областью определения
(ОДЗ)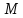 иобластью прибытия
иобластью прибытия называется правило
называется правило ,
в силу которого каждому числу
,
в силу которого каждому числу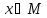 (аргумент) ставится в соответствие
некоторое число
(аргумент) ставится в соответствие
некоторое число (значение функции). Функция двух
переменных
(значение функции). Функция двух
переменных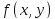 определяется также, но в качестве
определяется также, но в качестве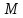 теперь берется некоторая область на
плоскости
теперь берется некоторая область на
плоскости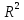 .
.
Примеры.
а) Функция ,
заданная формулой
,
заданная формулой ,
не является ни отображениемна(отрицательные числа не имеют прообразов),
ни взаимно однозначным (
,
не является ни отображениемна(отрицательные числа не имеют прообразов),
ни взаимно однозначным ( ,
но
,
но ).
Однако, если эту же формулу рассматривать
как отображение
).
Однако, если эту же формулу рассматривать
как отображение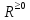 на
на ,
то оно будет биективным, и обратным
отображением к нему будет
,
то оно будет биективным, и обратным
отображением к нему будет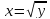 .
.
б)
Функции
 и
и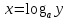 взаимно обратны. Первая отображает
взаимно обратны. Первая отображает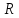 на
на ,
а вторая наоборот.
,
а вторая наоборот.
в)
Функция синуса не является взаимно
однозначно. Если
 сузить на отрезок
сузить на отрезок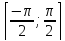 ,
то она биективно отображает этот отрезок
на отрезок
,
то она биективно отображает этот отрезок
на отрезок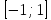 и обратным отображением служит
и обратным отображением служит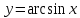 .
.
Самой
простой функцией является тождественная
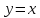 .
Ее график – биссектриса первого и
третьего квадрантов. Отправляясь от
такой функции с помощью арифметических
операций можно получить любой многочлен.
Если допустить и операцию деления, то
из тождественной функции можно получить
любую рациональную функцию, т.е. отношение
двух многочленов. Значения рациональной
функции можно вычислить вручную, в
отличие от значений трансцендентных
функций –
.
Ее график – биссектриса первого и
третьего квадрантов. Отправляясь от
такой функции с помощью арифметических
операций можно получить любой многочлен.
Если допустить и операцию деления, то
из тождественной функции можно получить
любую рациональную функцию, т.е. отношение
двух многочленов. Значения рациональной
функции можно вычислить вручную, в
отличие от значений трансцендентных
функций –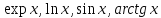 .
.
Можно
задавать функцию таблицей из двух строк,
где в первой строке перечислены все
возможные аргументы, а во второй –
соответствующие им значения. В математике
чаще прибегают к аналитическому способу
задания функции. Опишем процесс
построения аналитического выражения.
Пусть
 фиксированные функции, каждая из которых
возможно зависит от нескольких переменных.
Числом
фиксированные функции, каждая из которых
возможно зависит от нескольких переменных.
Числом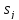 обозначим количество переменных функции
обозначим количество переменных функции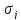 .
Тогда аналитическим выражением с базой
.
Тогда аналитическим выражением с базой и множеством переменных
и множеством переменных называется функция
называется функция ,
построенная в соответствие со следующим
рекуррентным правилом:
,
построенная в соответствие со следующим
рекуррентным правилом:
 для какого-либо
для какого-либо ,
где
,
где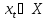 -- переменные;
-- переменные; для какого-либо
для какого-либо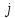 ,
где все
,
где все -- аналитические выражения.
-- аналитические выражения.
Если
база состоит только из трех типов
функций:
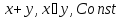 ,
а переменная одна,
,
а переменная одна, ,
то класс аналитических выражений
совпадает с многочленами одной переменной.
Если расширим базу двуместной операцией
деления
,
то класс аналитических выражений
совпадает с многочленами одной переменной.
Если расширим базу двуместной операцией
деления ,
то получим семейство дробно-рациональных
функций вида
,
то получим семейство дробно-рациональных
функций вида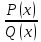 (см. далее). Если же базу дополнить еще
и функциями
(см. далее). Если же базу дополнить еще
и функциями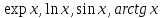 ,
то получимкласс элементарных функций.
,
то получимкласс элементарных функций.
Естественной
ОДЗ аналитического выраженияназывается
совокупность всех чисел, при которых
все операции, входящие в аналитическое
выражение определены, и получается
итоговый результат -- .
.
Пример.
Естественная ОДЗ функции есть отрезок
есть отрезок .
.
Декартовы координаты на плоскости
На
плоскости выберем точку
 (начало координат), единицу масштаба и
две взаимно перпендикулярные прямые,
проходящие через точку
(начало координат), единицу масштаба и
две взаимно перпендикулярные прямые,
проходящие через точку ,
которые превратим в оси с началом
,
которые превратим в оси с началом .
Все это и называется декартовой системой
координат. Каждая точка
.
Все это и называется декартовой системой
координат. Каждая точка на плоскости получит пару координат
на плоскости получит пару координат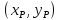 .
Соответствие между точками на плоскости
и декартовым квадратом
.
Соответствие между точками на плоскости
и декартовым квадратом будет биективным. Расстояние между
точками
будет биективным. Расстояние между
точками и
и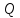 находится по формуле
находится по формуле

Принцип Декарта: любое уравнение вида

задает
кривую на плоскости состоящую из всех
точек, координаты которых удовлетворяют
данному уравнению. Именно так и
определяется график функции
 .
Наоборот, кривые на плоскости (прямые,
окружности, эллипсы, гиперболы, параболы
и т.д.), определяемые в геометрических
терминах, задаются аналитически
уравнением вида (2)
.
Наоборот, кривые на плоскости (прямые,
окружности, эллипсы, гиперболы, параболы
и т.д.), определяемые в геометрических
терминах, задаются аналитически
уравнением вида (2)
Примеры.
Уравнение вида ,
где
,
где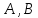 одновременно не равны 0, задает прямую
на плоскости и каждая прямая на плоскости
задается таким уравнением. Окружность
радиуса
одновременно не равны 0, задает прямую
на плоскости и каждая прямая на плоскости
задается таким уравнением. Окружность
радиуса с центром в точке
с центром в точке задается уравнением
задается уравнением
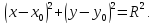
Области на плоскости задаются либо одним неравенством вида
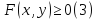
либо системой таких неравенств.
Примеры.
Неравенство вида ,
где
,
где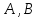 одновременно не равны 0, задает
полуплоскость и каждая полуплоскость
задается таким неравенством. Круг
радиуса
одновременно не равны 0, задает
полуплоскость и каждая полуплоскость
задается таким неравенством. Круг
радиуса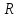 с центром в точке
с центром в точке задается неравенством
задается неравенством
