Тема 18 Степенные ряды

Функциональные ряды.

Ряд вида

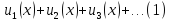
называется функциональным. Областью сходимости этого ряда называется множество всех чисел 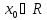при которых числовой ряд 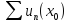сходится.

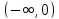Примеры 1. Ряд имеет интервал своей областью сходимости.

2. Ряд имеет область сходимости .

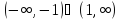Пусть D - подмножество множества действительных чисел. Говорят, что ряд (1) сходится к функции 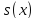, определенной на D равномерно, если для любого 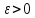найдется номер N такой, что для всякого натурального 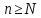и для всякого выполняется неравенство 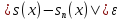. Здесь 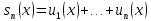-- частичные суммы ряда (1).

Пример 3. Имеет место равенство

для любого 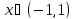; при этом сходимость не является равномерной на всем интервале (-1,1) и даже на полуинтервале 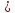, но является таковой на отрезке , где -- некоторое положительное число меньшее 1. Действительно, -ый остаток этого ряда выражается и оценивается при 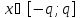как

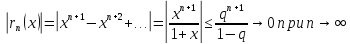
Так как б.м. величина не зависит от 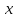, то функциональный ряд будет равномерно сходится на отрезке .

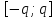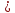Докажем теперь, что ряд не сходится равномерно на полуинтервале . Это следует из неограниченности остатка на полуинтервале . Какое бы 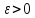и какое бы натуральное число 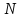мы ни взяли, найдется 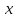достаточно близкое к -1 c условием .

Ряд (1) называется мажорируемым на области D, если существует сходящийся числовой ряд такой, что для любого n и для любого .

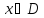Теорема. Если ряд (1) мажорируем и члены ряда непрерывны, то и функция непрерывна.

Доказательство. Пусть – мажоранта, 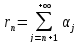. Справедлива оценка

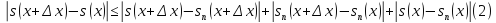
Фиксируем точку . Для заданного числа найдем номер такой, что при любом 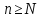. Тогда и при любом 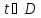и при любом Далее, выберем такое, что 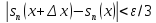при любом (пользуемся непрерывностью функции ). Тогда оценка (2) показывает, что □

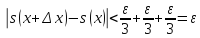Почленная дифференцируемость и интегрируемость функциональных рядов

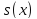Теорема о почленном интегрировании. Пусть ряд с непрерывными слагаемыми, мажорируем на отрезке и сходится к функции . Тогда

(тем самым числовой ряд в правой части (1) сходится).

Доказательство вытекает из оценки

где -- n-ый остаток мажоранты □

Теорема о почленном дифференцировании. Пусть 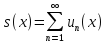, функции дифференцируемы и ряд мажорируем на отрезке . Тогда функция также дифференцируема на отрезке и имеет место равенство

Доказательство. Обозначим 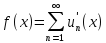. Тогда по предыдущей теореме

Отсюда следует равенство 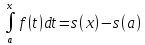. Левая часть в этом равенстве -- дифференцируемая функция, производная которой равна подынтегральной функции. Следовательно, □

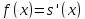Примеры. Применим к ряду , мажорируемому на отрезке , (мажоратна -- ), теорему о почленном интегрировании:

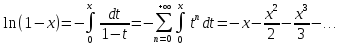
Применим к этому же ряду теорему о почленном дифференцировании

Для обоснования этой операции нужно установить мажорируемость ряда . Мажорантой для его на том же самом отрезке может служить числовой ряд , который сходится по признаку Даламбера.

К ряду 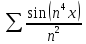нельзя применять теорему о почленном дифференцировании, так как в результате формального дифференцирования получается расходящийся (например, в точке x=0) ряд .

Степенные ряды.

Функциональный ряд вида

называется степенным рядом. Исследуем ряд (1) на абсолютную сходимость с помощью признака Даламбера:

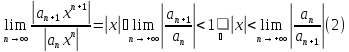
Обозначим

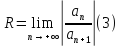
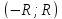и назовем это число радиусом сходимости. Из выкладок (2) и признака Даламбера вытекает, что ряд (1) абсолютно сходится при , т.е. в интервале и расходится при условии 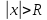. Поведение ряда (1) в точках исследуется особо.

Примеры. Ряд 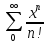имеет бесконечный радиус сходимости и, как мы потом увидим, его сумма совпадает с функцией 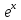. Ряд 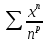имеет единичный радиус сходимости. При 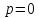в точках этот ряд расходится, а при 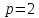этот ряд в точках 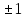сходится абсолютно. Ряд 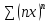имеет нулевой радиус сходимости, т.е. он сходится только в одной точке – 0.

Более общие степенные ряды, по степеням 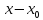имеют вид:

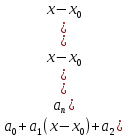
Линейной заменой переменной они сводятся к рядам вида (1). Интервалом абсолютной сходимости ряда (4) является , где – радиус сходимости ряда .

Дифференцирование и интегрирование степенного ряда

Пусть

-- степенной ряд с радиусом сходимости R.

Лемма 1. Ряд (1) мажорируем на любом отрезке [a,b] лежащем в интервале сходимости.

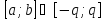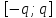Доказательство. Случай отбросим как тривиальный. Найдем такое, что . Тогда есть мажоранта ряда (1) на отрезке , а значит и на отрезке . □

Лемма 2. Ряд , полученный из ряда (1) почленным дифференцированием, имеет тот же радиус сходимости, что и исходный ряд.

Доказательство в предположении, что существует предел отношения следует из равенства

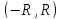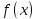Теорема. Пусть -- сумма ряда (1) на интервале . Функция бесконечно дифференцируема на этом интервале и её k-ая производная равна сумме k-ых производных членов ряда (1):

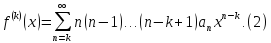
При этом ряд, стоящий в правой части (2) имеет тот же радиус сходимости R. Далее,

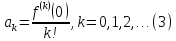
Кроме того, ряд (1) можно почленно интегрировать на любом отрезке 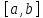, лежащем в интервале сходимости. В частности,

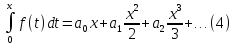
для любого 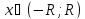и ряд, стоящий в правой части (4), имеет тот же радиус сходимости .

Ряды Тейлора и Маклорена

Вспомним формулу Тейлора:

Пусть здесь 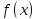-- бесконечно дифференцируемая функция. Тогда степенной ряд

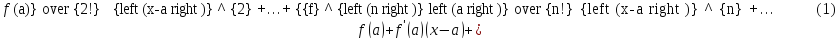
называется рядом Тейлора функции 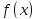в окрестности точки 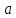. В частном случае, когда , этот ряд называют рядом Маклорена.

Предложение. Ряд Тейлора (1) сходится к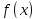 тогда и только тогда, когда .

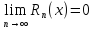Вообще говоря, ряд Тейлора может расходится в точках сколь угодно близких к точке или может сходится, но не к функции . Например функция

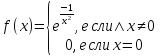
бесконечно дифференцируема в нуле и имеет все производные равные нулю. Следовательно, ряд Маклорена этой функции - нулевой, и его сумма не равна .

Определение. Если ряд (1) сходится к функции в окрестности точки , то функцию называют аналитической в этой точке. Аналитичность функции на множестве означает аналитичность в каждой точке этого множества.

Разложение элементарных функций в ряд Маклорена.

а) Разложение экспоненты

Для всех имеет место равенство

Для доказательства равенства (2) убеждаемся, что

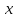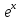при любом фиксированном и любых величинах . Далее применяем предложение предыдущего параграфа. По другому докажем равенство (2): как функция , так и сумма ряда в (2) - решения дифференциального уравнения с начальным условием y(0)=1. Из теоремы единственности решения дифференциального уравнения следует, что в этом случае функции совпадают.

б) Разложение гармоник

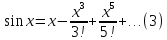
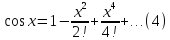
Равенства (3) и (4) можно доказать так же как и в а), взяв дифференциальное уравнение с начальными условиями y(0)=0, y'(0)=1 для функции sin x и y(0)=1, y'(0)=0 для функции cos x. Можно поступить и иначе: подставить в разложение (2) вместо 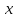чисто мнимое число , а далее приравнять действительные и мнимые части - получим в точности (3) и (4).

Заметим, что во всех трех равенствах (2),(3),(4) радиус сходимости ряда, стоящего справа равен бесконечности, т.е. разложения имеют место на всей числовой оси.

в) Биномиальное разложение

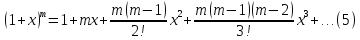
Здесь -- параметр. Исследуем сходимость ряда (5):

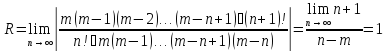
Итак, разложение (5) имеет место для всех 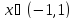, ибо как функция так и сумма ряда в (5) удовлетворяют дифференциальному уравнению 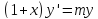с начальными условиями y(0)=1.

Отметим частные случаи разложения (5).

Пусть m - натуральное число. Тогда в ряду, стоящем в (5), остается лишь первые m+1 слагаемых, -- остальные равны нулю. Получаем равенство

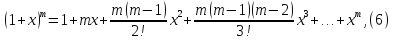
которое называется биномом Ньютона. Коэффициенты многочлена в правой части (6) называются биномиальными. Имеет смысл для любого действительного числа m и для любого целого неотрицательного числа n определить биномиальный коэффициент:

Нетрудно сосчитать: что 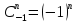, поэтому

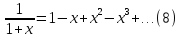
Далее, вычисляя

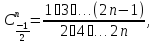
получим:

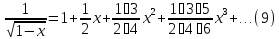
Подставляя в (9) вместо и интегрируя на отрезке , где 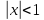получим:

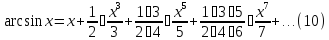
При левая часть в (10) также равна правой (следует применить вторую теорему Абеля):

г) Разложение логарифмической функции.

Интегрируя (8) на отрезке 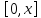при условии 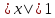, получим:

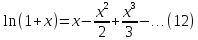
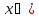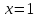Это равенство верно при любом . В частности, при имеем:

Для достижения точности надо взять 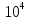слагаемых в ряду (13). Иначе, можно воспользоваться формулой

в которую подставим так, чтобы 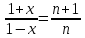. Тогда

В частности, при n=1 получаем:

Для достижения точности достаточно взять пять слагаемых, ибо ...

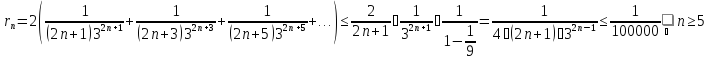
Тогда

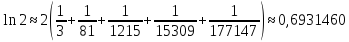
(Точное значение равно 0,6931471…)

Применение степенных рядов

Вычислим интеграл :

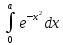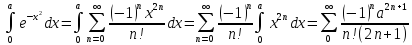
Решим дифференциальное уравнение c начальным условием . Полагая и подставляя этот ряд в дифференциальное уравнение, а затем почленно интегрируя, а затем приравнивая коэффициенты при одинаковых степенях, получим

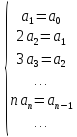
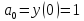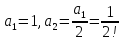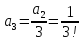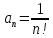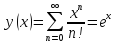Так как , то последовательно находим коэффициенты , и т.д. . Получаем . Полученный ряд имеет бесконечный радиус сходимости. Это оправдывает операцию почленного дифференцирования при любом .