ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Оглавление

1Определение определенного интеграла 1

2Свойства определённого интеграла 4

3Критерий интегрируемости Дарбу 10

4Формула Ньютона-Лейбница 12

5Замена переменной и интегрирование по частям в определённом интеграле 14

6Несобственные интегралы 15

6.1Теорема сравнения. 18

6.2Абсолютная сходимость 21

7Интегралы, зависящие от параметра 23

8Гамма-функция Эйлера 25

9Приближенное вычисление определённых интегралов 27

1. Определение определенного интеграла

Пусть функция 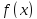определена на отрезке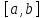и неотрицательна. Фигура, заданная неравенстваминазываетсякриволинейной трапецией(см. рис. 1). Вычислим площадь криволинейной трапеции. Идея вычисления состоит в том, чтобы нарезать эту трапецию на узенькие вертикальные полоски, площадь каждой полоски считать как площадь прямоугольника, а затем сложить получившиеся результаты. Мы получим приближенный ответ. Для получения точного ответа надо брать полоски все уже и уже и перейти к пределу, когда максимальная ширина полоски стремится к нулю. Вычислим таким образом площадь под экспонентой, если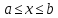. Возьмём равномерное разбиение отрезка [a,b]: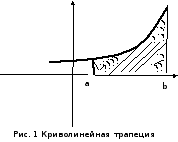

;

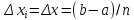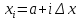
Тогда заменяя каждую полоску на прямоугольник с высотой равной значению экспоненты в левом конце основания полоски, получим суммарную площадь всех полосок, очевидно превосходящую площадь криволинейной трапеции под экспонентой:

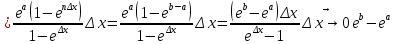
Здесь использована формула суммы геометрической прогрессии, а также эквивалентность бесконечно малых 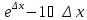при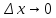. Так как функция e^xнепрерывна, то доказано, что S=e^b-e^a.

Пример.Вычислим площадь под параболойна отрезке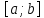(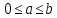). Возьмем разбиение вида (1) этого отрезка, а отмеченные точки выберем так:

Ясно, что , ибо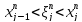, что в свою очередь эквивалентно

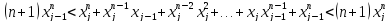
Тогда интегральная сумма вычисляется просто:

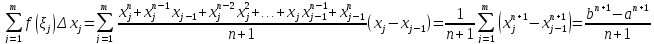
и предел этих интегральных сумм как предел константы равен . Это и есть площадь под параболой.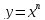

Перейдем к точным определениям. Разбиением отрезканазывается семейство точектаких, что

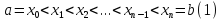
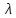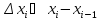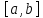Параметром разбиения(обозначим его) называется наибольшее из приращенийкогда индекспробегает от 1 до n. Пусть- функция, определенная на отрезкеи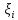- какие-либо точки из отрезков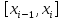которые назовемотмеченными. Тогда

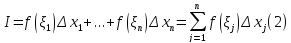
называется интегральной суммой.

Определение.Определённым интегралом функциина отрезкеназывается предел интегральных сумм, если параметр разбиения стремиться к нулю:

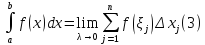
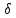Это значит, что определенный интеграл есть такое число , что для любого сколь угодно малогонайдется такое(зависящее от), что для любого разбиения (1) с параметроминтегральная сумма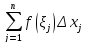отличается от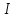меньше чем на:

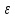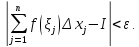
Функция 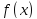называется подинтегральной,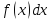называется подинтегральным выражением. Числоназывается нижним пределом интегрирования, а– верхним пределом интегрирования.

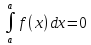Распространим понятие интеграла на случай отрезка, вырождающегося в точку, полагая по определению . Распространим понятие интеграла также на тот случай, когда нижний предел больше верхнего; считаем по определению

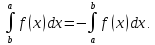
Так как предел не всегда существует, то и определенный интеграл на отрезке существует не от любой функции. Необходимым условием существования интегралаявляется ограниченность функциина отрезке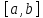. Действительно, если функция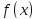неограничена, например, сверху, то при любом разбиении, каков бы ни был малый его параметр, найдутся отмеченные точки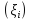такие, что интегральная сумма (2) больше чем любая наперед заданная величина. Следовательно, конечного предела интегральные суммы иметь не могут.

Основываясь на вычислении площади под параболой 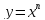, мы можем вычислить интеграл от многочлена, не прибегая к формуле Ньютона-Лейбница:

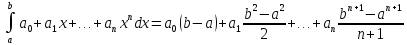
Критерий Коши интегрируемости функции. Ограниченная функция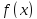на отрезке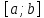интегрируема в том и только том случае, когда для любого𝜺>0найдетсяδ>0, что при любых двух разбиениях вида (1) с параметрамиинтегральные суммы различаются (по модулю) менее чем на𝜺.

??? Док-во

Функцию 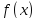, заданную на отрезке, для которой предел (3) существует, назовеминтегрируемой (по Риману)на этом отрезке. Пространство интегрируемых функций на отрезке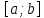обозначим.