5. Замена переменной и интегрирование по частям в определённом интеграле

Замена переменной. Пусть-- дифференцируемое отображениеcнепрерывной производной и такое, что, а-- непрерывная функция, заданная на отрезке. Тогда

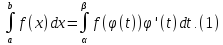
Доказательство. Пусть -- первообразная функции. Тогда по формуле замена переменной в неопределенном интеграле функцияесть первообразная функции. Применим формулу Ньютона-Лейбница дважды:

-- что и требовалось доказать. □

Пример 1.Вычислим площадь верхнего полукруга радиусаR.

Интегрирование по частям. Пустьи-- дифференцируемые функции на отрезке. Тогда

Доказательство. Соотношение проинтегрируем отдоbполучим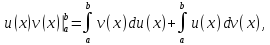что эквивалентно (2).

Пример 2.Вычислим

Заметим, что при условии

6. Несобственные интегралы

Пусть функция задана на полуинтервале, где, а величинаможет быть как конечным числом, так и. Предположим, чтоинтегрируема на любом отрезке,. Полагаем по определению

и называем это число несобственным интегралом. В случае, когда предел (1) существует, то говорим, что соответствующий интегралсходится; в противном случае будем говорить, что онрасходится.

Несобственный интеграл (1) применяется в двух типичных ситуациях.

1) Пусть . Тогда

2) Пусть d∈ℝи функциянеограничена на полуинтервале.

Если на полуинтервале, то несобственный интеграл равен площади неограниченной фигуры -- криволинейной трапеции, ограниченной сверху графиком функции, снизу – осью Ох и слева – вертикальной прямой (см. рис. 1)

Отметим, что если функцияна самом деле интегрируема на отрезке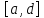(это означает, в частности, что), то коллизии обозначений не возникает -- несобственный интеграл в смысле (1) будет равен определенному интегралу функциина отрезке.

Аналогично определяется несобственный интеграл для функций, определенных на полуинтервале , гдеи:

В примере §5 мы фактически вычислили несобственный интеграл.

Cвойство линейности несобственных интегралов.Если интегралысходятся, то для любых чиселkиmсходится также и интеграл, и он равен.

Это свойство вытекает из свойства линейности предельного перехода.

Свойство аддитивности несобственных интегралов. Пустьинтегрируема на отрезкедля фиксированногои любоготакого, что. Выберем точку. Несобственный интеграл сходится в том и только том случае, если сходится несобственный интегралПри этом условии имеет место равенство

Формула Ньютона-Лейбница для несобственных интегралов. Пусть-- первообразная непрерывной функциина интервале (c,d). Предположим, что существуют пределы

Тогда несобственный интеграл сходится, причём

Равенство (5) вытекает из формулы Ньютона-Лейбница для обычных интегралов и соотношений (4).

Пример 1. Вычислим

Пример2. Докажем ???

1. Теорема сравнения.

Пусть на интервале. Тогда

1. если сходится, тосходится;

2. если расходится, то расходится.

Доказательство. 1) Если сходится, то существует (конечная) площадь криволинейной трапеции Т под графиком функции. Криволинейная трапеция под графиком функциисодержится в Т, следовательно и у нее площадь также конечна. Тем самым интегралсходится.

2) следует из 1) в силу логического принципа: импликация эквивалентна импликации(черта сверху – отрицание утверждения). Более подробно: если бы интеграл сходился, то и интеграл также бы сходился, согласно первому утверждению. Это, однако, противоречит условию. Противоречие показывает, что интеграл должен расходится.□

Следствие.Пусть функции кусочно непрерывны и имеют неотрицательные значения на полуинтервале. Предположим, что существует пределпричём он отличен от 0. Тогда интегралыиведут себя одинаково в смысле сходимости, т.е. либо оба сходятся, либо оба расходятся.

Аналогичное утверждение имеет место для полуинтервала (c,b].

Предложение об "эталонных" интегралах . Пусть a>0.

1. Интеграл сходится тогда и только тогда, когда p>1.

2. Интеграл сходится тогда и только тогда, когдаp<1.

Доказательство. 1. Если, то первообразная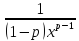подинтегральной функцииимеет конечный предел 0 при. По формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интегралсходится и равен.

Если , то первообразной подинтегральной функции служит, который не имеет конечного предела на. Длято же самое можно сказать о первообразной.

Аналогично, прямыми вычислениями доказывает второе утверждение.

Примеры

1. Интегралсходится, так как здесьТогда и интегралбудет сходится, ибо на бесконечности имеет место асимптотическая оценка:

2. Исследуем на сходимость . Так какпри x→0, а интегралсходится (здесь-- см. предложение об эталонных интегралах, пункт 2), то и исходный интеграл сходится.

2. Докажем, что интегралы исходятся и вычислим их. Имеем

Интеграл также сходится, ибо занесение под знак дифференциалаи заменапревращают его в интеграл, который сходится согласно предложению об эталонных интегралах и равен 1.

Интегралы ирасходятся, так как такая же замена приводит их к несобственным эталонным интегралами, с