2. Сумма ряда

Ряд

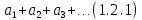
имеет общий член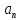ипоследовательность частичных сумм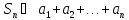Ряд (1.2.1) называют сходящимся к числуS, если.

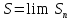Следствие теоремы о пределе монотонной последовательности.Ряд с неотрицательными слагаемыми сходится тогда и только тогда, когда последовательность частичных сумм ограничена сверху.

2. Число е

Теорема 1.Предел последовательности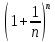существует и заключен между числами 2 и 3.

Доказательство. Обозначим 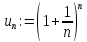. Если вычислять значения последовательности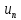, то видим, что

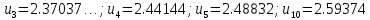
Видим, что эта последовательность возрастает. Докажем этот факт. Используя бином Ньютона, получим:

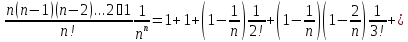
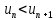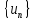При переходе к следующему члену последовательности каждый из сомножителей 1-k/n в правой части (1) увеличивается, а кроме того, добавляется еще одно (n+2)-е слагаемое. Итак, доказано, что, т.е. последовательностьмонотонно возрастает. Далее, если ограничить сверху каждый из сомножителей 1-k/n единицей, а 1/k! ограничить сверху, то

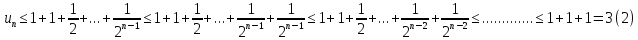
Итак, последовательность монотонно возрастает и ограничена сверху числом 3, следовательно, по аксиоме о пределе монотонно возрастающей и ограниченной сверху последовательности эта последовательность имеет предел, причем он меньше либо равен 3 по свойству ПР7.

Так как 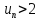, то по свойству ПР7 следует, что это предел больше либо равен 2.□

Определение. Предел последовательности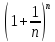обозначают e и называютоснованием натуральных логарифмов или числом е.

Приближенное значение e≈2.718281828 (1828 -- год рождения Л.Н. Толстого). Чаще всего пользуются приближением e≈ 2.7.

Теорема 2.

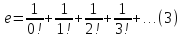
Доказательство. Оценку (2) можно применить и к частичным суммам 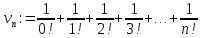. Отсюда следует ограниченность сверху последовательности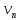, значит она имеет предел, т.е. ряд в (3) имеет сумму. Из формулы (1) следует, что эта сумма больше либо равна. ???

3. Предел функции

В этом параграфе изучается важнейшее понятие анализа – предел функции.

Примеры

Составим таблицу значений функци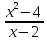и при

	1.9	1.95	1.98	1.99	1.999
	3.9	3.95	3.98	3.99	3.999

Заметим, что значение мы подставить не можем, так как получим неопределенность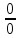. Тем не менее, понятно, что значения функции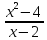приближаются к числу 4 по мере того, как значения аргумента приближаются к 2. Это станет совершенно очевидно, после сокращения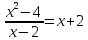. Правая часть здесь уже определена при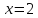и имеет значение 4. Иными словами, простым алгебраическим преобразованием мы раскрыли неопределенность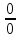и вычислили предел функци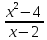ипри.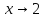

Рассмотрим еще один пример: вычислим предел 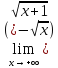. Преобразуем

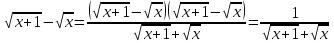
При неограниченном увеличении аргумента 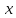знаменатель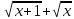становиться больше чем любое наперед заданное число. Так как, то получаем нулевое значение предела.

1. Определение и свойства предела функции.

Интервал 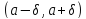называют δ-окрестностью точки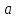(здесь δ >0). Она задается неравенством. Множество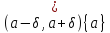называютпроколотой окрестностью точки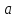. Она задается неравенством.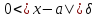

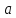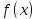Пусть функция определена в некоторой проколотой окрестности точки. Число A называется пределом функциипри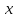стремящемся к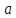, если чем ближе подходит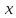к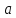тем меньше значение функции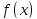отличается от своего предела. Мерой близост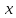ии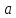можно считать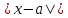. Однако мы не допускаем равенства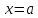, ибо функция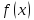может быть и неопределенной в точке.

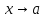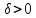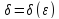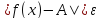Определение.Число A называетсяпределом функции при, если для любого положительного𝜺, найдется число, зависящее от() такое, чтодля всех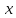принадлежащих проколотой δ-окрестности точки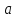, т.е. таких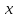, что.

Предложение 1.Если предел функции существует, то он единственен.

Доказательство такое же как и для предела последовательности.

Предел функции 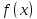призаписывают как. Формально,

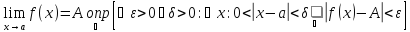
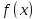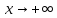Теперь приведем определение пределов на бесконечности. Число A называется пределом функции при, если для любого положительного𝜺найдется число C такое, что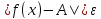для всехтаких, что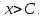Предел функци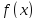ипри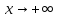записывают как.

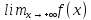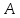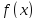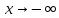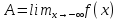Аналогично, число называется пределом функциипри(), если для любого положительного𝜺найдется C такое, что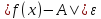для всех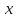, таких, что.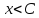

Иногда приходится рассматривать предел при дополнительных условиях, ограничениях на переменную 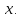Например, совершенно ясно, чт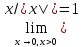о, ибо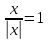при ограничении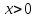. Аналогично,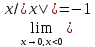. Найденные пределы называются односторонними, первый – предел справа, второй – предел слева. Заметим, что «двустороннего» предела функция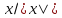при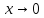не имеет.

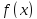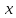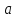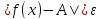Число A называется пределом функции пристремящемся к справа, если для любого положительного𝜺найдется δ =δ (𝜺)>0 такое, чтодля всех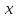таких, что.

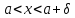Предел функци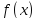и при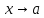справа записывают как.

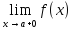Число A называется пределом функции при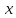 стремящемся к 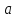слева(записываем как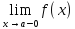), если для любого положительного𝜺найдется δ =δ (𝜺)>0 такое, что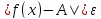для всех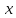таких что

Предложение 2.Предел функции существует тогда и только тогда, когда существуют оба односторонних предела, причем они совпадают.

Доказательство. Пусть 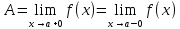. Тогда длянайдутся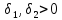такие, что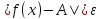для всех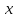таких что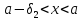и для всехтаких что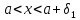. Взяв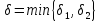, получим, что неравенствовыполняется для всех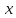из проколотой-окрестности точки. В обратном направлении утверждение есть очевидная тавтология.

Предел функции и предел последовательности связаны между собой как показывает следующее утверждение.

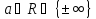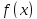Теорема 1.Пустьи-- функция, определенная в проколотой окрестности точки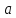. Тогда предел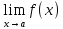существует и равен A в том и только том случае, когда для любой последовательности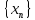точек сходящихся к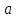и отличных от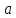, последовательность значений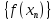сходится к A.

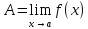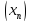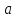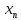Доказательство. Пусть ) и-- последовательность, сходящаяся к, причем для любогоnне равно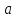. Возьмем какое-либо положительное𝜺и найдем для него δ >0 такое, что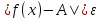как только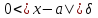. Так как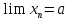, то найдется номер N такой, что для всех n>N имеет место неравенство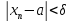. Тогда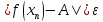. Это значит, что.

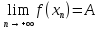Наоборот, пусть равенство не имеет места. Тогда

Взяв здесь последовательность , сходящуюся к нулю и выбрав для нее соответствующие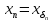, получим последовательность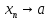, причем для любого n имеет место неравенство, поэтому предел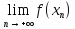не равенA.□