
- •Оглавление
- •Предел последовательности вещественных чисел
- •Свойства предела
- •Сумма ряда
- •Число е
- •Предел функции
- •Примеры
- •Определение и свойства предела функции.
- •Свойства предела функции
- •Бесконечно малые величины
- •Сравнение бесконечно малых величин.
- •Первый замечательный предел
- •Второй замечательный предел
- •Непрерывность функции
- •Свойства непрерывных функций
- •Непрерывность на отрезке
- •Принцип непрерывности
Свойства предела функции
Следующие свойства предела функции вытекают из аналогичных свойств предела последовательности с применением теоремы 2.
LIM1. Константная функция имеет предел, равный этой же константе
Пусть
существую пределы
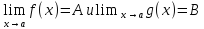 .
Тогда
.
Тогда
LIM2.
Предел суммы существует и равен сумме
пределов: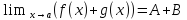 .
.
LIM3.
Предел произведения существует и равен
произведению пределов: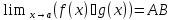 .
В частности, константу можно выносить
за знак предела.
.
В частности, константу можно выносить
за знак предела.
LIM4. Предел отношения существует и равен отношению пределов в том случае, когда предел знаменателя отличен от 0.
Следующие свойства LIM5-LIM7 описывают предельный переход в неравенствах.
LIM5.
Если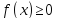 при любом x из некоторой малой окрестности
точки a, то и
при любом x из некоторой малой окрестности
точки a, то и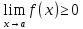 (при условии существования предела).
Аналогично свойство имеет место для
неравенства "≤ ".
(при условии существования предела).
Аналогично свойство имеет место для
неравенства "≤ ".
Как следствие предыдущего свойства получаем монотонность предела:
LIM6.
Предположим, что для любого
для любого близкого к a. Тогда и
близкого к a. Тогда и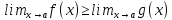 при условии существования этих пределов.
при условии существования этих пределов.
Следующее свойство называется теоремой о пределе промежуточной функции
LIM7.(предел промежуточной функции)Предположим, что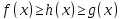 для любого
для любого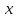 из некоторой проколотой окрестности
точки
из некоторой проколотой окрестности
точки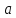 .
Предположим также, что пределы
.
Предположим также, что пределы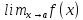 и
и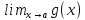 существуют и совпадают между собой.
Тогда и предел промежуточной функции
существуют и совпадают между собой.
Тогда и предел промежуточной функции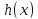 при
при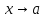 существует и совпадает с пределами
крайних функций.
существует и совпадает с пределами
крайних функций.
LIM8. (предел сложной функции) Предположим, что
существует предел
 равный
равный ;
;существует предел
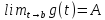 .
.
Тогда
существует предел сложной функции
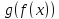 при
при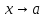 и он равен A.
и он равен A.
Доказательство.
Фиксируем
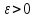 .
Находим
.
Находим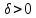 такое, что
такое, что для любого
для любого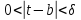 .
Для этого
.
Для этого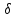 находим
находим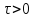 такое, что как только
такое, что как только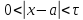 ,
то
,
то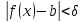 .
Тогда и неравенство
.
Тогда и неравенство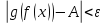 также будет выполнено для любого
также будет выполнено для любого ,
удовлетворяющего неравенствам
,
удовлетворяющего неравенствам .□
.□
Бесконечно малые величины
Функция
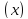 ,
определенная в некоторой проколотой
окрестности точки
,
определенная в некоторой проколотой
окрестности точки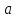 называется бесконечно малой при
называется бесконечно малой при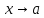 ,
если
,
если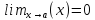 .
.
Свойства бесконечно малых величин вытекают из соответствующих свойств предела:
M1. Сумма бесконечно малых величин суть бесконечно малая величина.
Функция
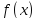 называется ограниченной в точке
называется ограниченной в точке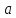 ,
если найдется такая окрестность этой
точки и такая константа
,
если найдется такая окрестность этой
точки и такая константа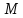 ,
что
,
что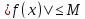 для
всех
для
всех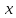 из этой окрестности.
из этой окрестности.
Предложение.Функция, имеющая предел в точке ,
ограничена в этой точке. Более того,
если
,
ограничена в этой точке. Более того,
если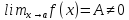 ,
то
,
то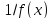 ограничена в точке a.
ограничена в точке a.
Доказательство.
Если
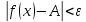 для любых
для любых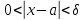 ,
то для любых
,
то для любых из -окрестности точки
из -окрестности точки имеет место оценка
имеет место оценка

Докажем
второе утверждение. Полагаем
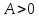 .
Для𝜺=A/2 найдем
δ такое, что
.
Для𝜺=A/2 найдем
δ такое, что . Тогда
. Тогда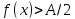 и
и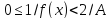 для всех x из δ-окрестности точки
для всех x из δ-окрестности точки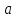 .
Аналогично разбирается случай A<0.□
.
Аналогично разбирается случай A<0.□
M2.
Произведение бесконечно малой
величины на функцию, ограниченную в
точке ,
является бесконечной малой величиной.
В частности, произведение б.м. на функцию,
имеющую предел в точке
,
является бесконечной малой величиной.
В частности, произведение б.м. на функцию,
имеющую предел в точке суть также б.м., а также произведение
нескольких б.м. есть б.м.
суть также б.м., а также произведение
нескольких б.м. есть б.м.
М3. Произведение б.м. на константу есть б. м.
M4.Отношение б.м. к функции, имеющий
ненулевой предел в точке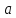 является б.м.
является б.м.
Действительно,
если
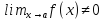 ,
то
,
то ограничена в точке a по выше доказанному
в предложении. Следовательно, на основании
свойства М2 получаем, что
ограничена в точке a по выше доказанному
в предложении. Следовательно, на основании
свойства М2 получаем, что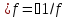 также есть б.м.
также есть б.м.
М5.
Пусть(x) - бесконечно
малая при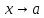 ,
а
,
а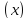 -- функция такая, что выполняется
неравенство
-- функция такая, что выполняется
неравенство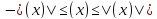 для всех x из достаточно малой проколотой
окрестности точки
для всех x из достаточно малой проколотой
окрестности точки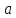 .
Тогда
.
Тогда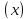 также будет б.м.
также будет б.м.
Это свойство верно в силу теоремы о пределе промежуточной функции.
