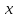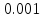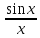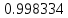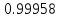- •Оглавление
- •Предел последовательности вещественных чисел
- •Свойства предела
- •Сумма ряда
- •Число е
- •Предел функции
- •Примеры
- •Определение и свойства предела функции.
- •Свойства предела функции
- •Бесконечно малые величины
- •Сравнение бесконечно малых величин.
- •Первый замечательный предел
- •Второй замечательный предел
- •Непрерывность функции
- •Свойства непрерывных функций
- •Непрерывность на отрезке
- •Принцип непрерывности
Сравнение бесконечно малых величин.
Две
функции (x) и(x) называютсяэквивалентными при
 (записываем это как
(записываем это как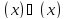 ),
если предел их отношения при
),
если предел их отношения при равен единице. Чаще всего это определение
применяют к б.м. величинам. Отношение
эквивалентности функций обладает
свойствами:
равен единице. Чаще всего это определение
применяют к б.м. величинам. Отношение
эквивалентности функций обладает
свойствами:
симметричность (если ∼, то и∼),
транзитивность (если ∼и∼γ, то∼γ );
рефлексивность (т.е. ∼)
Пусть
теперь (x),(x) -- б.м. при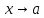 .
Если
.
Если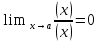 ,
то(x) называетсяб.м. высшего порядка малости по сравнению
с (x); записывают
это так(x)=o((x)) (читается: величина альфа есть о-малая
от величины бэта). Бесконечно малыеиимеютодин
порядок малости, если указанный выше
предел существует и не равен 0. Отношение
"иметь один порядок малости" также
есть отношение эквивалентности, т.е.
выполняются свойства a), b),c) выше. Если
,
то(x) называетсяб.м. высшего порядка малости по сравнению
с (x); записывают
это так(x)=o((x)) (читается: величина альфа есть о-малая
от величины бэта). Бесконечно малыеиимеютодин
порядок малости, если указанный выше
предел существует и не равен 0. Отношение
"иметь один порядок малости" также
есть отношение эквивалентности, т.е.
выполняются свойства a), b),c) выше. Если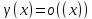 ,
то∼+γ . Действительно,
,
то∼+γ . Действительно,
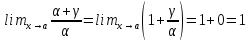
Предложение
1. Предел функции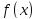 при
при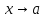 существует
и равен A тогда и только тогда, когда
существует
и равен A тогда и только тогда, когда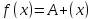 для некоторой б.м..
для некоторой б.м..
Доказательство.
Если
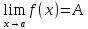 ,
то
,
то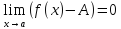 и
и есть искомая б.м. В другую сторону
утверждение вытекает из свойства предел
суммы.
есть искомая б.м. В другую сторону
утверждение вытекает из свойства предел
суммы.
Теорема 1.Функцию можно заменять на эквивалентную без изменения предела, если она стоит в качестве сомножителя в числителе или знаменателе.
Доказательство. Пусть ∼. Тогда
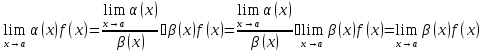
Аналогичное доказательство проходит для случая, когда истоят в знаменателе.□
Пример.Далее мы покажем, что при имеет место эквивалентность x∼sin x∼tg x. Тогда
имеет место эквивалентность x∼sin x∼tg x. Тогда

Первый замечательный предел
Составим
теперь табличку значений функции
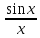 при
при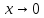 .
Так как
.
Так как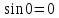 ,
то мы снова сталкиваемся с раскрытием
неопределенности “0/0” .
,
то мы снова сталкиваемся с раскрытием
неопределенности “0/0” .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы видим, что значения функции приближаются к единице по мере того, как аргумент стремится к нулю. Однако никакое алгебраическое преобразование нам не поможет раскрыть эту неопределенность. Прибегая к оценкам площадей фигур и свойствам предела, мы докажем, что
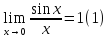
На
рис.
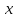 -- длина дуги
-- длина дуги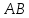 .
Из рисунка видно, что при
.
Из рисунка видно, что при имеют место неравенства
имеют место неравенства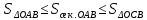
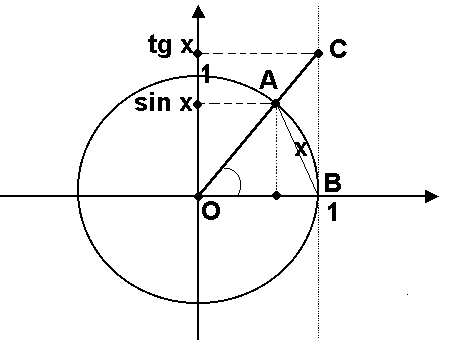
Но
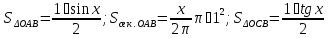
Отсюда
получаем неравенства
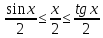 .
Поделим все части этого неравенства
на
.
Поделим все части этого неравенства
на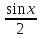 >0,
получим
>0,
получим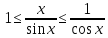 .
Обратим дроби и выводим
.
Обратим дроби и выводим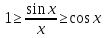 .
Отметим также, что заодно мы доказали
неравенство
.
Отметим также, что заодно мы доказали
неравенство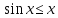 при
при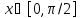 .
Так как функции
.
Так как функции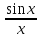 и
и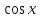 четные, то для любых ненулевых
четные, то для любых ненулевых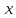 с модулем меньше π /2 имеют место
неравенства
с модулем меньше π /2 имеют место
неравенства
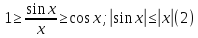
Тогда
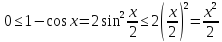
--
стремится к 0, откуда
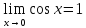 . Левая часть двойного неравенства в
(2) также имеет предел равный 1. По теореме
о пределе промежуточной функции получаем
требуемое равенство.
. Левая часть двойного неравенства в
(2) также имеет предел равный 1. По теореме
о пределе промежуточной функции получаем
требуемое равенство.
Второй замечательный предел
Теорема.Существует предел функции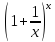 при
при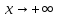 и оно равен e. Это же число е равно пределу
функции
и оно равен e. Это же число е равно пределу
функции при
при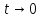 .
.
Докажем
это равенство, используя теорему о
связи предела последовательности и
предела функции. Пусть
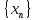 -- последовательность точек, сходящихся
к +∞ . Можно считать, что
-- последовательность точек, сходящихся
к +∞ . Можно считать, что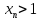 для всех n так, что
для всех n так, что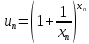 определено.
Имеем:
определено.
Имеем:
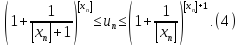
Так как
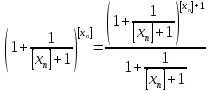
и
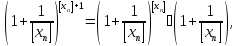
то
пределы крайних последовательностей
в (4) существуют и равны основанию
натуральных логарифмов e. Тогда по
свойству LIM7 получаем, что предел
последовательности
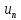 существует
и равен e.
существует
и равен e.
Этот предел можно переписать и по другому:

Сделав
замену
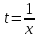 получаем еще одну формулировку второго
замечательного предела
получаем еще одну формулировку второго
замечательного предела
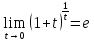
Таблица эквивалентных б.м. приx→0
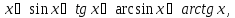
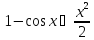

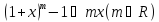
Обоснуем
эти эквивалентности. Эквивалентности
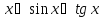 вытекают из первого замечательного
предела. Далее
вытекают из первого замечательного
предела. Далее
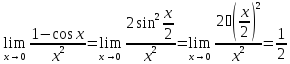
доказывает
эквивалентность
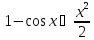 .
Выкладка
.
Выкладка
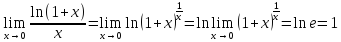
--
доказывает эквивалентность
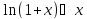 .
Здесь мы воспользовались вторым
замечательным пределом и непрерывностью
логарифма, которую докажем позже.
.
Здесь мы воспользовались вторым
замечательным пределом и непрерывностью
логарифма, которую докажем позже.

Здесь
сделана замена
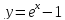 ,
откуда
,
откуда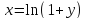 .
Аналогично, с заменой, доказываются
оставшиеся эквивалентности.
.
Аналогично, с заменой, доказываются
оставшиеся эквивалентности.