
- •Оглавление
- •Предел последовательности вещественных чисел
- •Свойства предела
- •Сумма ряда
- •Число е
- •Предел функции
- •Примеры
- •Определение и свойства предела функции.
- •Свойства предела функции
- •Бесконечно малые величины
- •Сравнение бесконечно малых величин.
- •Первый замечательный предел
- •Второй замечательный предел
- •Непрерывность функции
- •Свойства непрерывных функций
- •Непрерывность на отрезке
- •Принцип непрерывности
Предел и непрерывность.
Оглавление
1Предел последовательности вещественных чисел 1
1.1Свойства предела 4
1.2Сумма ряда 6
2Число е 7
3Предел функции 8
Примеры 8
3.1Определение и свойства предела функции. 9
3.2Свойства предела функции 12
4Бесконечно малые величины 14
5Сравнение бесконечно малых величин. 15
6Первый замечательный предел 17
7Второй замечательный предел 18
7.1Таблица эквивалентных б.м. при x→ 0 19
8Непрерывность функции 20
8.1Свойства непрерывных функций 20
9Непрерывность на отрезке 22
9.1Принцип непрерывности 26
Предел последовательности вещественных чисел
Неравенство
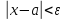 задает интервал
задает интервал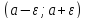 ,
который называется𝜺
-окрестностью точки (числа)
,
который называется𝜺
-окрестностью точки (числа)
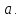 Заметим, что любой интервал, содержащий
точку
Заметим, что любой интервал, содержащий
точку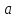 ,
включает в себя
,
включает в себя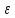 -окрестность
при достаточно малом
-окрестность
при достаточно малом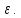
Последовательностью называется ряд чисел
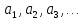
занумерованный
натуральными числами (или целыми
неотрицательными числами). Формально,
последовательность есть отображение
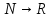 .
Число
.
Число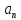 называетсяn-ым членом
(или общим членом) последовательности
называетсяn-ым членом
(или общим членом) последовательности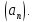 Очень часто он задается аналитическим
выражением.
Очень часто он задается аналитическим
выражением.
Примеры последовательностей
а)
константная последовательность:
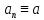 ;
;
б)
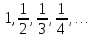 .
Общий член задается формулой
.
Общий член задается формулой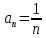 .
.
в)
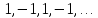 . Общий член задается формулой
. Общий член задается формулой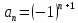 .
.
г)
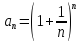 .
Эта последовательность вида
.
Эта последовательность вида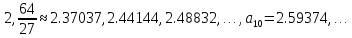 Видно, что эта последовательность
монотонно возрастает.
Видно, что эта последовательность
монотонно возрастает.
Определение.Число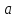 называетсяпределом последовательности
называетсяпределом последовательности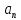 ,
если для любого положительного𝜺найдется натуральное N такое, что
,
если для любого положительного𝜺найдется натуральное N такое, что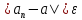 для всех
для всех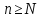 .
.
Пример
1.Докажем, что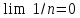 .
Возьмём𝜺>0.
Неравенство
.
Возьмём𝜺>0.
Неравенство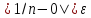 выполнено, если n>1/𝜺. В качестве N(𝜺) можно взять [1/𝜺]+1 -- наименьшее натуральное число,
превосходящее 1/𝜺. Здесь через
выполнено, если n>1/𝜺. В качестве N(𝜺) можно взять [1/𝜺]+1 -- наименьшее натуральное число,
превосходящее 1/𝜺. Здесь через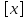 обозначена целая часть числа
обозначена целая часть числа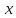 ,
т.е. наибольшее целое число, не превосходящее
,
т.е. наибольшее целое число, не превосходящее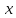 .
.
Пример
2.Докажем, что последовательность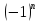 не имеет предела. Действительно, пусть
не имеет предела. Действительно, пусть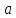 -- предел этой последовательности. Тогда
для
-- предел этой последовательности. Тогда
для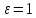 и достаточно большого
и достаточно большого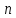 имеют место неравенства
имеют место неравенства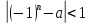 и
и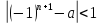 .
Иными словами
.
Иными словами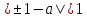 .
Отсюда
.
Отсюда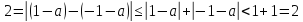 -- противоречие.
-- противоречие.
Предложение 1.Если предел существует, то он единственен.
Доказательство.
Пусть числа A и B равны пределу
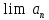 .
Если
.
Если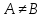 ,
то взяв
,
то взяв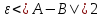 получим непересекающиеся окрестности
получим непересекающиеся окрестности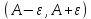 и
и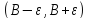 .
Но согласно определению предела, начиная
с некоторого
.
Но согласно определению предела, начиная
с некоторого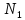 в первую окрестность попадают все
в первую окрестность попадают все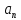 и начиная с некоторого
и начиная с некоторого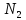 во вторую попадают все
во вторую попадают все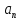 .
Возьмем
.
Возьмем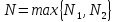 .
Тогда
.
Тогда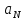 – общая точка этих окрестностей;
противоречие. Противоречие показывает,
что предположение
– общая точка этих окрестностей;
противоречие. Противоречие показывает,
что предположение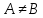 неверно. Следовательно,
неверно. Следовательно,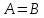 .
.
После
доказательства единственности предела
имеем право ввести оператор предельного
перехода:
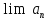 .
.
Теорема
1.Любая монотонно возрастающая
ограниченная сверху последовательность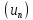 имеет предел и он равен
имеет предел и он равен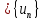 .
Аналогично, любая монотонно убывающая
и ограниченная снизу последовательность
имеет предел равный точной нижней грани
множества значений этой последовательности.
.
Аналогично, любая монотонно убывающая
и ограниченная снизу последовательность
имеет предел равный точной нижней грани
множества значений этой последовательности.
Доказательство.
Пусть
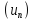 -- монотонно возрастающая и ограниченная
сверху последовательность. Обозначим
-- монотонно возрастающая и ограниченная
сверху последовательность. Обозначим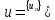 .
Пусть𝜺>0.
Так как число u-𝜺не является верхней гранью значений
нашей последовательности, то найдется
натуральное N такое, что
.
Пусть𝜺>0.
Так как число u-𝜺не является верхней гранью значений
нашей последовательности, то найдется
натуральное N такое, что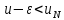 .
Тогда для любого n≥ N имеем
.
Тогда для любого n≥ N имеем
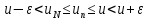
в
силу монотонности последовательности
и того факта, что u -- верхняя грань. Отсюда
для любого
натурального
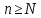 следует неравенство
следует неравенство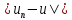 <𝜺,
что и требовалось доказать.□
<𝜺,
что и требовалось доказать.□
Свойства предела
ПР1.Предел суммы двух последовательностей равен сумме пределов, если пределы слагаемых существуют.
Пусть
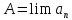 ,
,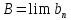 .
Фиксируем𝜺>0. Находим
.
Фиксируем𝜺>0. Находим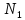 такое, что для любого
такое, что для любого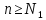 выполняется неравенство
выполняется неравенство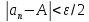 .
Аналогично, находим
.
Аналогично, находим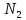 такое, что для любого
такое, что для любого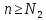 выполняется неравенство
выполняется неравенство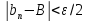 .
Тогда для любого
.
Тогда для любого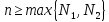 выполняется оценка
выполняется оценка
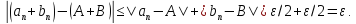
ПР2.Предел константной последовательности равен этой константе.
Последовательность
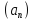 называется ограниченной, если найдется
константа
называется ограниченной, если найдется
константа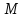 такая, что
такая, что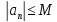 для всех
для всех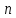 .
.
ПР3.
Любая сходящаяся последовательность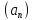 ограничена.
ограничена.
Действительно,
пусть
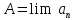 . Для𝜺=1 найдем
натуральное N, начиная с которого
выполняется неравенство
. Для𝜺=1 найдем
натуральное N, начиная с которого
выполняется неравенство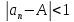 .
Тогда
.
Тогда
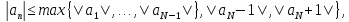
что и требовалось доказать.
ПР4.Предел произведения равен произведению пределов, при условии, что пределы сомножителей существуют.
Доказательство.
Пусть
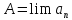 и
и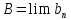 .
Ограничим последовательность
.
Ограничим последовательность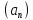 числом M>0 согласно свойства ПР3. Будем
иметь:
числом M>0 согласно свойства ПР3. Будем
иметь:
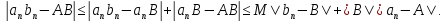
Так
как величины
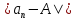 и
и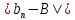 могут быть сделаны сколь угодно малыми,
то и
могут быть сделаны сколь угодно малыми,
то и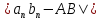 также можно сделать меньше наперед
заданного𝜺для всех n, начиная с некоторого
натурального N.
также можно сделать меньше наперед
заданного𝜺для всех n, начиная с некоторого
натурального N.
ПР5.Константу можно выносить за знак предела: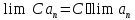
Это утверждение есть следствие свойств ПР4 и ПР2.
ПР6.Предел отношения равен отношению пределов, если пределы числителя и знаменателя существуют и последний не равен нулю.
Достаточно
доказать, что
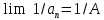 в
предположении
в
предположении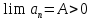 и далее применить свойство Г. Из условия
следует, что найдется N начиная с которого
и далее применить свойство Г. Из условия
следует, что найдется N начиная с которого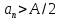 .
Тогда модуль разности
.
Тогда модуль разности
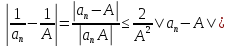
может быть сделан сколь угодно малой величиной начиная с некоторого N. □
На
основе предела
 можно вычислять другие пределы, пользуясь
уже не определением, а правилами ПР1-ПР6.
Например,
можно вычислять другие пределы, пользуясь
уже не определением, а правилами ПР1-ПР6.
Например,
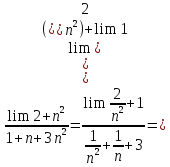
Опишем теперь предельные переходы в неравенствах.
ПР7.Если выполняется неравенство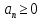 начиная с некоторого N, и предел
последовательности
начиная с некоторого N, и предел
последовательности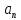 существует, то
существует, то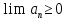 .
Аналогичное свойство имеет место для
неравенства ≤ .
.
Аналогичное свойство имеет место для
неравенства ≤ .
Действительно,
если
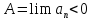 ,
то для
,
то для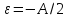 найдется N, начиная с которого
найдется N, начиная с которого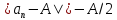 .
Тогда
.
Тогда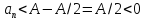 -- противоречие с условием.□
-- противоречие с условием.□
Заметим, что для строгих неравенств аналогичное утверждение несправедливо. Например, 1/n>0 для любого n, но lim 1/n=0, как мы доказали выше.
ПР8.
Если выполняется неравенство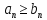 начиная с некоторого N, то
начиная с некоторого N, то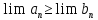 при условии, что эти пределы существуют.
при условии, что эти пределы существуют.
Действительно,
так как
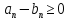 для всех
для всех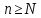 ,
то
,
то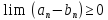 согласно свойства ПР7. Тогда, применяя
свойства ПР1 и ПР5, получим:
согласно свойства ПР7. Тогда, применяя
свойства ПР1 и ПР5, получим:
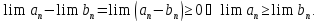
ПР9
(предел промежуточной последовательности).
Если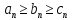 начиная с некоторого номера, а пределы
крайних последовательностей существуют
и равны одному и тому же числу A, то предел
начиная с некоторого номера, а пределы
крайних последовательностей существуют
и равны одному и тому же числу A, то предел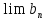 также существует и равен A.
также существует и равен A.
Доказательство.
Пусть число 𝜺>0 задано. Тогда найдется номер N такой,
что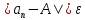 и
и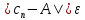 начиная с N. Отсюда
начиная с N. Отсюда
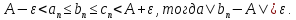
Пример.
Докажем, что если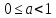 ,
то
,
то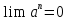 .
В силу монотонного убывания
.
В силу монотонного убывания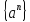 и ограниченности снизу нулем, предел
этой последовательности существует по
теореме о пределе монотонной
последовательности. Применяя принцип
Архимеда, получаем, что
и ограниченности снизу нулем, предел
этой последовательности существует по
теореме о пределе монотонной
последовательности. Применяя принцип
Архимеда, получаем, что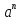 сколь угодно близко подходит к 0. Тогда
сколь угодно близко подходит к 0. Тогда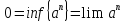 .
.
