6. Інтеграл Лебега від необмежених невід’ємних вф

Нехай як і раніше A - простір з скінченою мірою, функція - ВФ а також майже всюди скінчена, а також на. Позначимо череззрізку функції , що визначається рівністю:. Вимірність цієї функції очевидна, оскільки вона слідує з рівності:.

Лема 1.	(Міра точок необмеженості функції)
	Для функції, що визначена вище має місце рівність: .

Доведення. , а тому з неперервності зверху маємо:, оскільки за умовою функція майже всюди скінчена.

Лема доведена.

Оскільки усі зрізки функції - обмежені ВФ, а тому вони інтегровані за Лебегом. З того, щослідує, що, а тому існує скінчена чи нескінченна границя

. (1)

Якщо границя (1) скінчена, то функція називаєтьсяінтегрованою за Лебегом, або сумовною, а її інтеграл Лебега визначається рівністю: . Якщо ж границя(1) нескінченна, то за означенням покладемо: .

Якщо - обмежена ВФ, то при достатньо великих, а тому інтеграл для обмеженої ВФ дає за обома значеннями ті ж самі значення.

Лема 2.	(достатня ознака існування ІЛ для необмежених функцій)
	Нехай - невід’ємні ВФ іна, та функція- сумовна на. Тоді функціятакож сумовна ната справджується нерівність:
	.	(2)

Доведення. З умови слідує, що . Згідно теореми про ІЛ для нерівних функцій та визначенню ІЛ для необмеженої функції маємо:

. (3)

з цієї нерівності слідує скінченність границі , а тому й сумовність. Переходячи до границі прив нерівності(3), одержимо потрібну нерівність (2).

Лема доведена.

Якщо - інтегрована нафункція,- вимірна множина. Тоді- ВФ, при цьому, а тому з леми 2 функціятакож сумовна, а тому природнім стає наступне означення.

Якщо множина - вимірна, а функція- сумовна на, то функціяназиваєтьсясумовною на множині , а її інтеграл по цій множині визначається рівністю: . Зрозуміло, що якщо функціясумовна на усьому просторі, то вона також сумовна на будь-якій вимірній підмножині цього простору.

Теорема 1.	(Лінійність ІЛ для необмежених функцій)
	Якщо - невід’ємні сумовні функції, тофункціятакож сумовна і.

Доведення. По черзі перевіримо адитивність та однорідність інтегралу Лебега.

, а тому можемо записати нерівності:

, а тому функція сумовна. Граничним переходом одержимо, що. З іншого боку,, а тому. Знову робимо граничний перехід і одержимо:. Ці дві нерівності й доводять адитивність ІЛ.

Тепер однорідність. При - очевидно. Нехай тепер. Тоді, а тому. Звідси слідує сумовність функції. Після граничного переходу ми маємо першу нерівність:

. А з того, що , то з сумованості вище доведеної функції одержимо, що, а після граничного переходу одержимо другу нерівність:, з якої слідує рівність при. Нехай. З того,

що , то функція- сумовна. Оскільки, то з доведеного вище маємо:, звідки й слідує потрібна рівність.

Теорема доведена.

Нехай деяка фіксована невід’ємна сумовна функція на. Розглянемо функціюдля довільної вимірної множини.

Теорема 2.	(Абсолютна неперервність ІЛ як функції множин)
	Якщо - невід’ємна сумовна функція, то функція множинабсолютно неперервна відносно міри, тобто:A .

Доведення. З визначення ІЛ для необмеженої невід’ємної ВФ слідує, що :. Якщо покласти, то для будь-якої ВМ, що задовольняє умову, одержимо:

.

Теорема доведена.

Теорема 3.	(Злічена адитивність ІЛ як функції множин)
	Якщо - невід’ємна сумовна функція, то функція множинзлічено адитивна, тобто якщо,A, то .

Доведення. Досить легко показати скінчену адитивність функції : якщо, то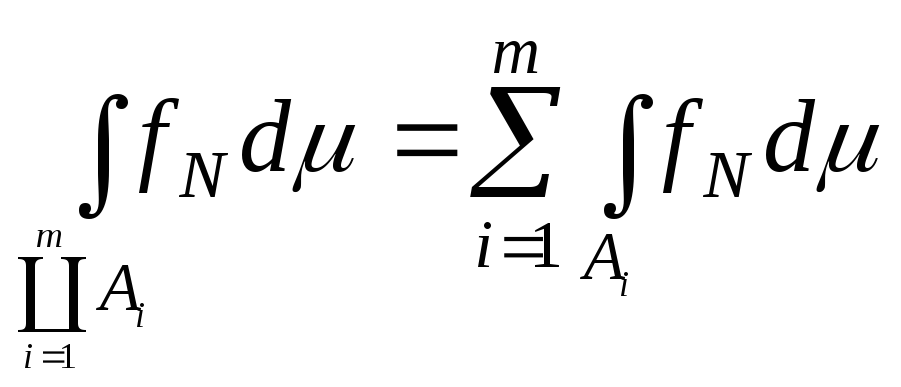. Далі граничним переходом отримаємо скінчену адитивність функції. З попередньої теореми:. Із зліченої адитивності міри, а тому:. А далі із скінченої адитивності маємо:, де останній доданок не перевищує. А тому.

Теорема доведена.

Нехай тепер функція вимірна майже всюди скінчена. Розглянемо від’ємну та додатну частини цієї функції:, які мають властивості – вони невід’ємні, також майже всюди скінченні та вимірні. Крім того. Для обох цих функцій визначено поняття інтегрованості за Лебегом, як для невід’ємних функцій, а тому природно дати таке визначення.

Функція називаєтьсясумованою (інтегрованою за Лебегом) на , якщо сумовна обидві функції . При цьому інтеграл Лебега від функціївизначається рівністю:.

Теорема 4.	(Модуль ІЛ та ІЛ від модуля довільної ВФ)
	Для сумованості ВФ необхідно й достатньо, щоб була сумована функція. При цьому їх інтеграли пов’язані нерівністю:.

Доведення. Необхідність. Нехай - сумовна, тоді також сумовані функції, але тоді з лінійності ІЛ для невід’ємних функцій сумована й функція. При цьому:.

Достатність. Нехай - сумована, тоді, а тому сумовані також і функції, а тому сумована й функція.

Далі маємо: .

Теорема доведена.

Наслідок.	(Достатня ознака існування ІЛ довільної ВФ)
	Якщо ВФ та, де- сумована функція, тотакож сумована функція.

Якщо - сумовна функція,- ВМ, тоді функція- також сумовна, оскільки. А тому природнім виглядає наступне визначення.

Якщо множина - вимірна, та функція- сумовна на, то функціяназиваєтьсясумовною на множині та її інтеграл визначається рівністю:

.

Теорема 5.	(Лінійність ІЛ для довільної необмеженої ВФ)
	Якщо - сумовні функції, тофункціятакож сумовна і.

Доведення. З простої нерівності слідує умовність функції.

Тепер адитивність. Якщо - сумовні, то оскільки, та. Прирівняємо останні два вирази і одержимо:

.

Усі функції невід’ємні. А тому для них можна скористатися властивістю лінійності:

, , що й доводить те що потрібно.

Нехай - сумовна функція,. Тоді,, а тому. Звідки і маємо однорідність для додатних. Тепер перевіримо для від’ємних, для цього достатньо перевірити для. Оскільки

Нехай задана деяка обмежена ВФ , розглянемо функцію множин, що для будь-якої вимірної множинизадається рівністю:

. (4)

Теорема 6.	(Злічена адитивність ІЛ для необмежених функцій)
	Функція множин злічено адитивна, тобто, якщо A, то

Теорема 7.	(Абсолютна неперервність ІЛ для необмеженої функції)
	Якщо - сумовна функція, то функція множин, що визначається формулою(4) абсолютно неперервна відносно міри .