4. Інтеграл Лебега від простих функцій

Нехай A - вимірний простір з скінченою мірою. проста вимірна функція, тобто

, (1)

, (2)

де - вимірні множини.

Інтеграл Лебега по множині (по простору ) функції позначається символом абота для простої функції(1),(2) визначається рівністю:

. (3)

Лема 1.	(Коректність визначення ІЛ для простих функцій)
	Попереднім означення ІЛ визначено коректно.

Доведення. Покажемо, що це визначення не залежить від вибору розбиття простору . Нехай в представленні(1) усі сталі різні, припустимо що в нас є інше представлення простору та простої функції:,. При такому поданні кожна з множинє об’єднанням тих множин, для яких. Далі з адитивності міри одержимо:

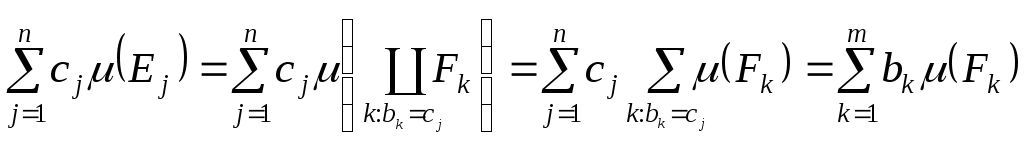, що й доводить коректність визначення.

Лема доведена.

Якщо - вимірна множина,- її ХФ, тоді

.

Нехай задана довільна вимірна множина . Якщо- проста ВФ, то добутоктакож проста ВФ, що дає змогу визначитиінтеграл Лебега від простої ВФ по будь-якій множині:

. (4)

Розглянемо випадок основного простору ,L – клас усіх лебегівських множин простору ,- міра Лебега. Тоді інтеграл по відрізкупозначається якабо аналогічно до інтегралу Рімана, а інтеграл по будь-якій вимірній підмножинічерез.

Теорема 1.	(Лінійність)
	Якщо прості ВФ,, то.

Доведення. Нехай ,,,. Легко зрозуміти за побудовою, що функціяприймає значенняна множині, а тому, деДалі просто з визначення інтегралу та адитивності міри одержимо:

.

Теорема доведена.

Теорема 2.	(ІЛ від невід’ємної функції)
	Якщо проста ВФ і, то.

Доведення. Нехай , тоді невід’ємність функції майже всюди означає, що якщо, то, а тому.

Теорема доведена.

Наслідок 1.	(ІЛ від нерівних функцій)
	Нехай прості ВФ і, то.

Для доведення достатньо застосувати теорему для функції .

Наслідок 2.	(Двобічна оцінка ІЛ)
	Якщо - проста ВФ іна ВМ, то .

Наслідок 3.	(ІЛ від нульової функції)
	Якщо проста ВФ і, то.

Достатньо в попередньому наслідку покласти .

Наслідок 4.	(ІЛ від рівних функцій)
	Нехай прості ВФ і, то.

Наслідок 5.	(ІЛ від модуля)
	Якщо проста ВФ, то

Нехай деяка фіксована проста ВФ. Визначимо наалгебріL вимірних множин числову функцію L за формулою

,L. (5)

Зрозуміло, що . Дослідимо інші властивості функції.

Теорема 3.	(Злічена адитивність ІЛ по проміжку інтегрування)
	Функція множин , що визначається формулою(5) злічено адитивна, тобто якщо ,L, то , при цьому ряд у правій частині рівності збігається абсолютно.

Доведення. Нехай ,. Із зліченої адитивності міри та з одержаних вище властивостей, маємо:

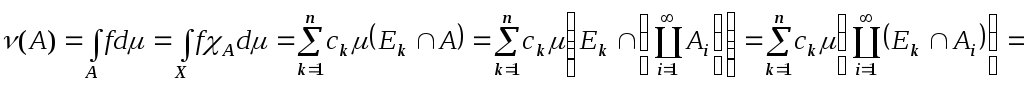
. В правій частині ми маємо лінійну комбінацію збіжних знакосталих рядів, а тому можна довільним чином міняти місцями порядок додавання, і одержаний ряд буде абсолютно збіжним. Далі маємо:

.

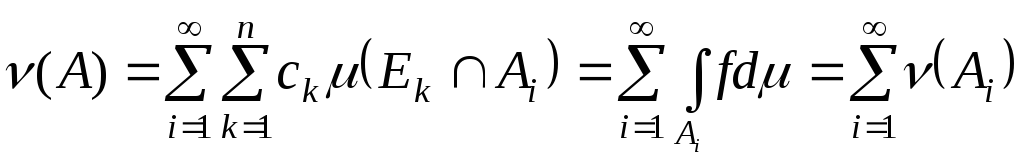Теорема доведена.

Функція L називається абсолютно неперервною відносно міри , якщо :L: .

Теорема 4.	(Про абсолютну неперервність ІЛ)
	Функція множин , що визначається формулою(5) є абсолютно неперервною функцією множин відносно міри .

Доведення. Нехай проста ВФ,. Тодіпокладемо. Тоді примаємо:.

Теорема доведена.