
- •Министерство образования и науки Российской Федерации
- •Введение
- •1. Элементы математической логики
- •1.1. Высказывания и операции над ними
- •1.2. Формулы логики высказываний. Равносильность формул
- •1.3. Предикаты и кванторы
- •Упражнения
- •2. Теория множеств
- •2.1. Основные понятия
- •2.2. Операции над множествами
- •Упражнения
- •3. Комбинаторика
- •3.1. Общие правила комбинаторики
- •3.2. Размещения, сочетания и перестановки без повторения (без возвращения)
- •3.3. Размещения, сочетания и перестановки с повторением (с возвращением)
- •Упражнения
- •4. Теория вероятностей
- •4.1. Историческая справка
- •4.2. Случайные события
- •4.3. Определения вероятности
- •4.4. Операции над вероятностями
- •4.5. Формула полной вероятности. Формула Байеса.
- •Формула Байеса.
- •Упражнения
- •5. Элементы математической статистики
- •5.1 Понятие случайной величины
- •5.2. Виды распределений
- •5.3 Числовые характеристики случайной величины
- •Упражнения
- •6. Обработка результатов эксперимента
- •6.1. Основные положения
- •6.2. Способы представления экспериментальных данных
- •2. Графическое представление экспериментальных данных.
- •6.3. Понятие о корреляционной зависимости
- •Упражнения
- •7. Лабораторные работы (краткое содержание)
- •Математические основы шкалирования. Формы представления информации
- •Формы представления информации
- •Закон нормального распределения и его характеристика
- •Корреляционный анализ
- •Регрессионный анализ (линейная регрессия)
- •Некоторые методы математической обработки экспериментальных данных
- •Бронникова Лариса Михайловна
- •Колмогорова Валентина Мироновна
- •Основы математической
- •Обработки информации
1.2. Формулы логики высказываний. Равносильность формул
Логическая формула – запись сложного высказывания в виде простых высказываний, соединенных операциями отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции и скобок.
В случае, если в логической формуле присутствуют несколько операций, не разделенных скобками, то порядок выполнения операций следующий:
отрицание;
конъюнкция;
дизъюнкция;
импликация;
эквиваленция.
Формула называется тавтологией, если она истинна при любых значениях истинности, входящих в нее высказываний.
Например,
рассмотрим возможные значения истинности
формулы ![]() .
Построим таблицу истинности для данной
формулы.
.
Построим таблицу истинности для данной
формулы.
-
А
В

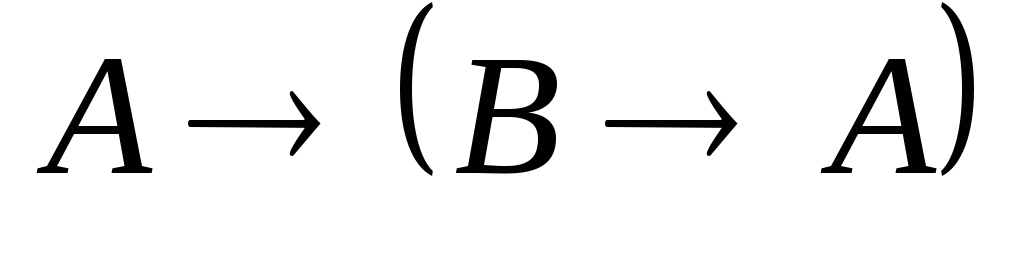
1
1
1
1
1
0
1
1
0
1
0
1
0
0
1
1
Формула всегда только истинна, значит является тавтологией.
Формула называется противоречием, если она ложна при любых значениях истинности, входящих в нее высказываний.
Например,
рассмотрим возможные значения истинности
формулы ![]() .
Построим таблицу истинности для данной
формулы.
.
Построим таблицу истинности для данной
формулы.
-
А
В
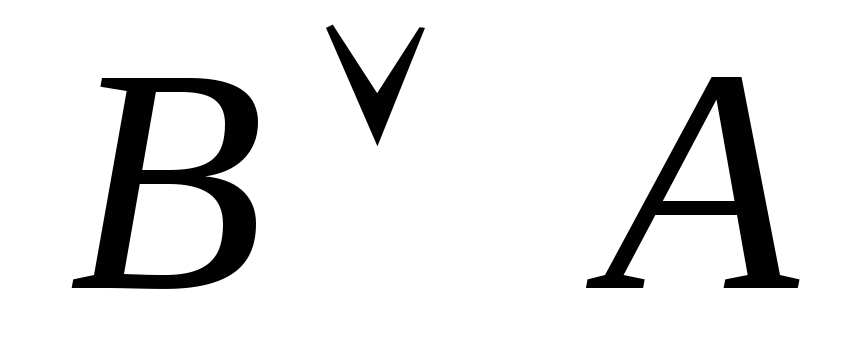

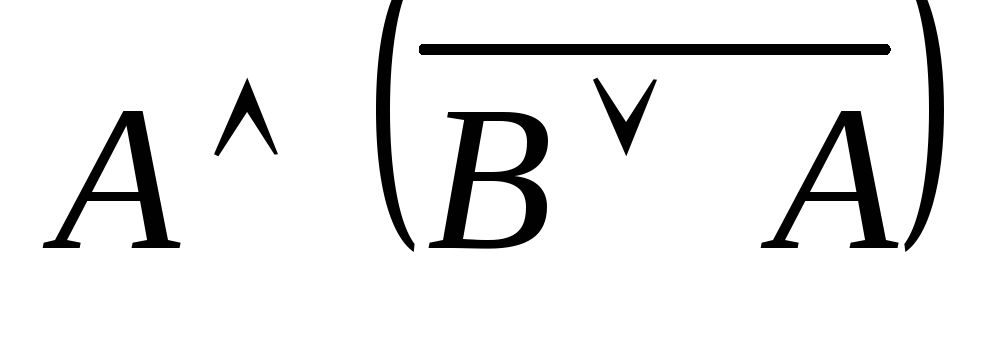
1
1
1
0
0
1
0
1
0
0
0
1
1
0
0
0
0
0
1
0
Формула всегда только ложна, значит является противоречием.
Формулы называются равносильными, если при любых значениях истинности высказываний, в них входящих, значения истинности формул совпадают.
Для обозначения
равносильности формул используют знак
![]() .
Для
выяснения равносильности формул для
них строят таблицы истинности.
.
Для
выяснения равносильности формул для
них строят таблицы истинности.
Например,
доказать равносильность формул ![]() и
и ![]() .
.
Отразим в таблице истинности значения истинности каждой формулы.
-
А
В



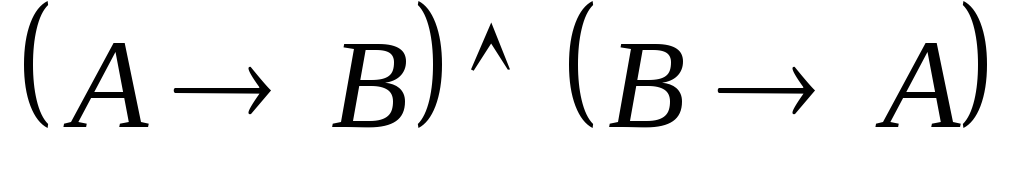
1
1
1
1
1
1
1
0
0
0
1
0
0
1
0
1
0
0
0
0
1
1
1
1
Значения
истинности формул при одинаковых
значениях истинности высказываний А
и В совпадают (выделенные столбцы), что
дает право утверждать равносильность
формул, значит ![]() .
.
Аналогично можно показать, что имеют место следующие равносильности, которые называют законами логики:
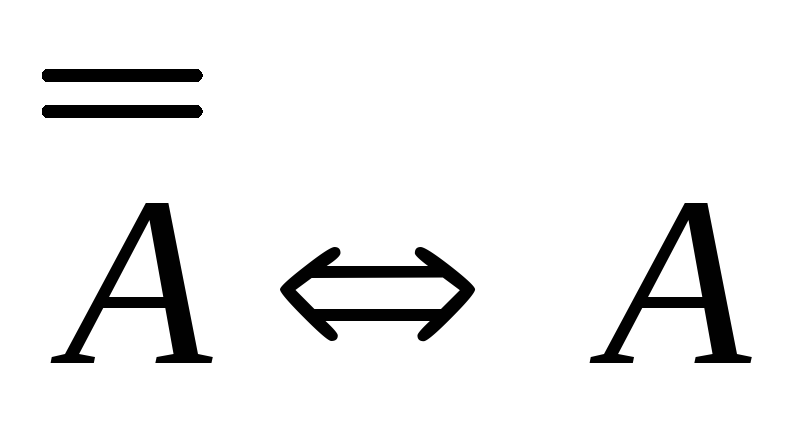 (закон
двойного отрицания);
(закон
двойного отрицания); (закон
коммутативности конъюнкции);
(закон
коммутативности конъюнкции); (закон
коммутативности дизъюнкции);
(закон
коммутативности дизъюнкции); (закон
ассоциативности конъюнкции);
(закон
ассоциативности конъюнкции); (закон
ассоциативности дизъюнкции);
(закон
ассоциативности дизъюнкции);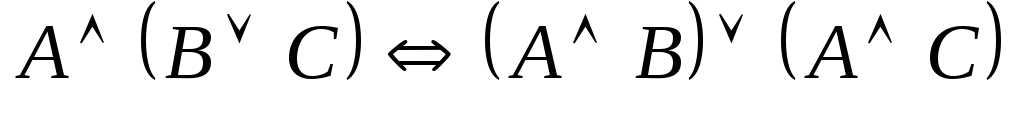 (закон
дистрибутивности конъюнкции относительно
дизъюнкции);
(закон
дистрибутивности конъюнкции относительно
дизъюнкции);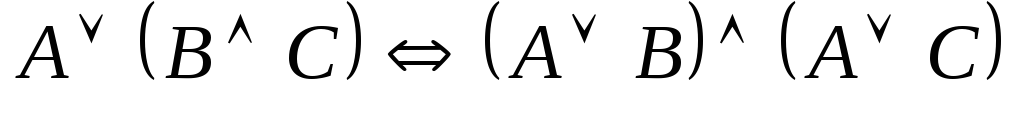 (закон
дистрибутивности дизъюнкции относительно
конъюнкции);
(закон
дистрибутивности дизъюнкции относительно
конъюнкции); (закон
де Моргана);
(закон
де Моргана); (закон
де Моргана);
(закон
де Моргана); (закон контрапозиции);
(закон контрапозиции);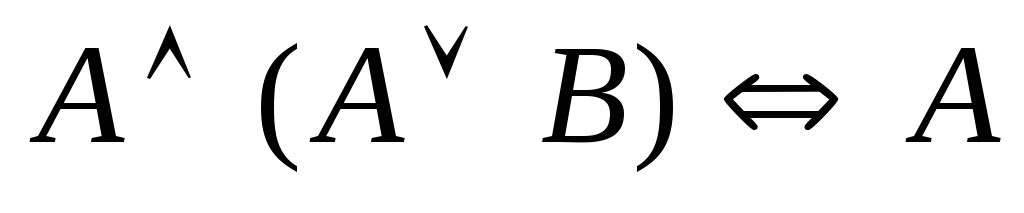 (закон поглощения);
(закон поглощения);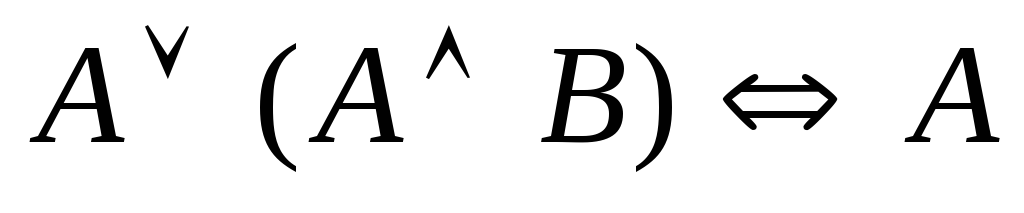 (закон поглощения);
(закон поглощения);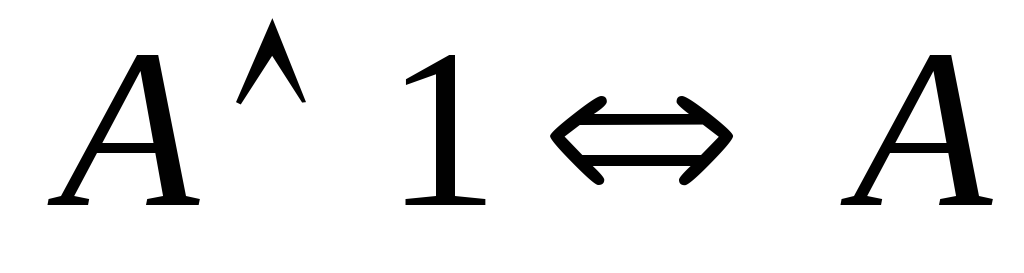 ;
;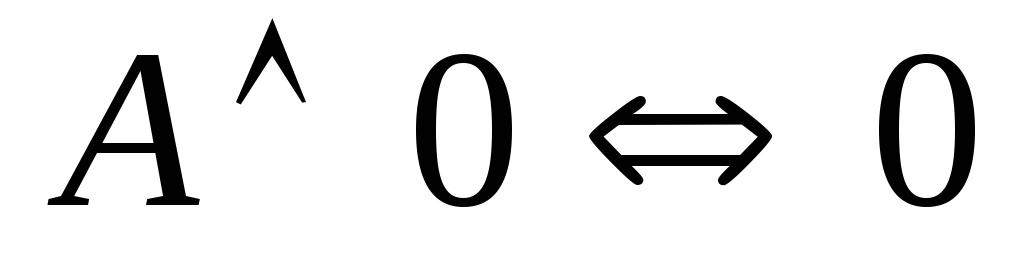 ;
;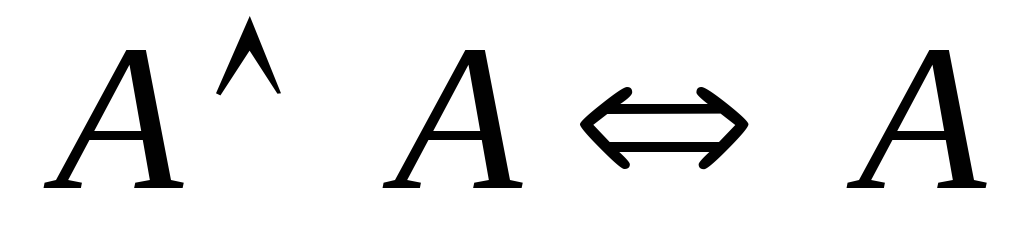 ;
;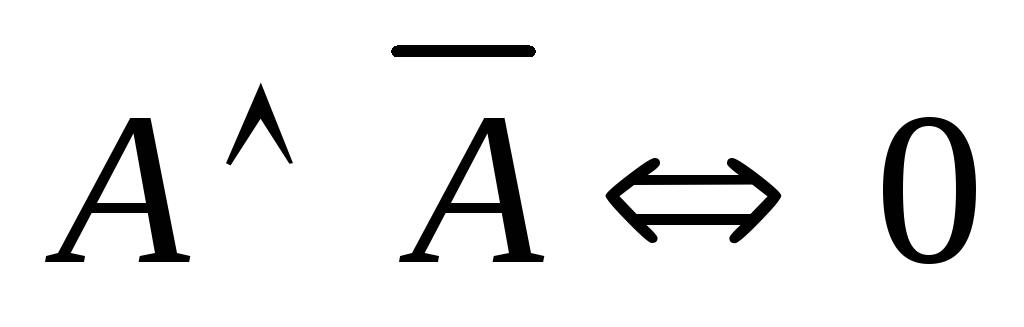 (закон противоречия);
(закон противоречия);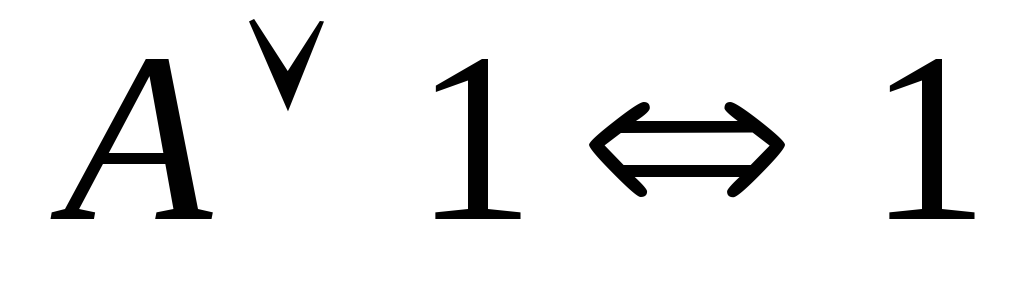 ;
;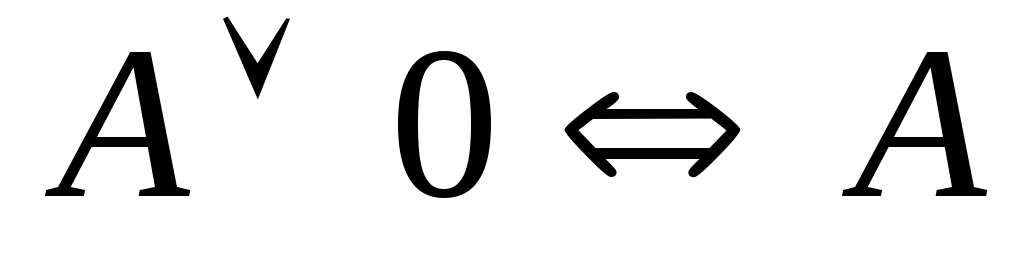 ;
;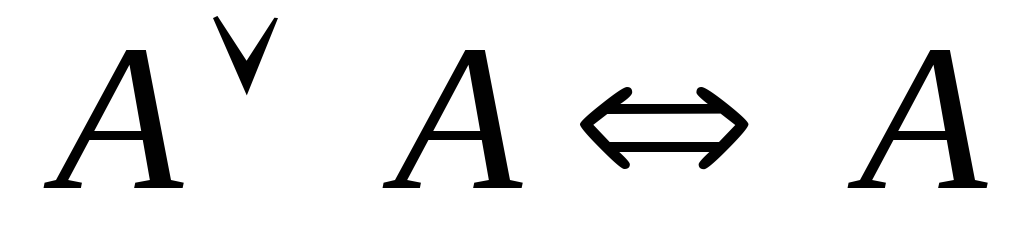 ;
;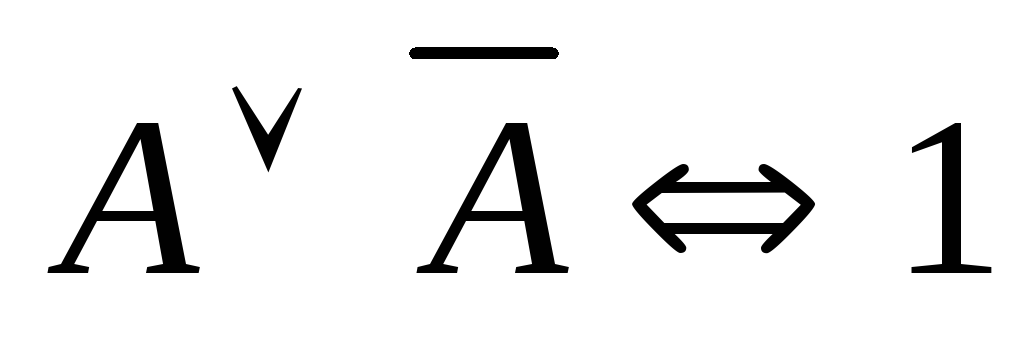 (закон исключенного
третьего);
(закон исключенного
третьего);
1.3. Предикаты и кванторы
Предикат – это предложение с переменными, которое после замены переменных определенными их значениями превращается в высказывание.
Если
предикат содержит одну переменную х,
то его обозначают ![]() ,
если
предикат содержит две переменные х
и у,
то его обозначают
,
если
предикат содержит две переменные х
и у,
то его обозначают
![]() и
т.д.
и
т.д.
Например:
а)
![]() :
«х
– четное число» является предикатом;
:
«х
– четное число» является предикатом;
б) любое уравнение или неравенство является предикатом.
Для предикатов аналогично определены те же операции, что и для высказываний.
Например:
а) система уравнений или неравенств – конъюнкция предикатов;
б) совокупность уравнений или неравенств – дизъюнкция предикатов.
Существуют 2 вида кванторов:
Квантор всеобщности. Обозначается
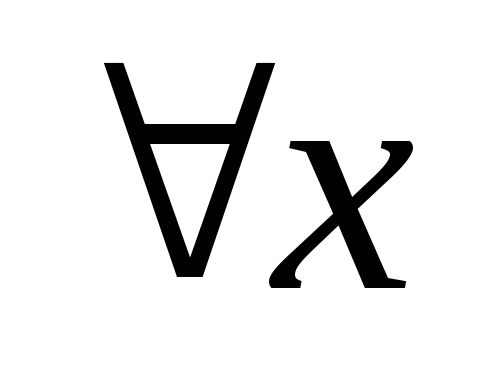 .
Запись
.
Запись
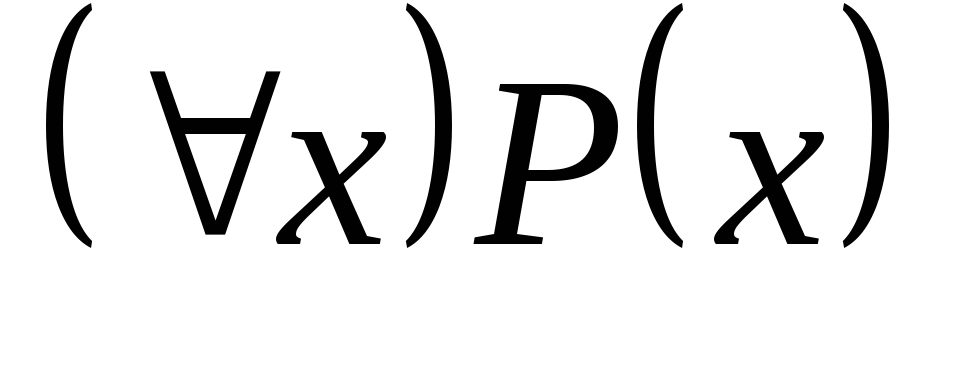 читается как «Для любого
х выполняется
Р(х)»
или «Для всех
х верно
Р(х)»
или «Для каждого
х
Р(х)».
читается как «Для любого
х выполняется
Р(х)»
или «Для всех
х верно
Р(х)»
или «Для каждого
х
Р(х)».Квантор существования. Обозначается
 .
Запись
.
Запись
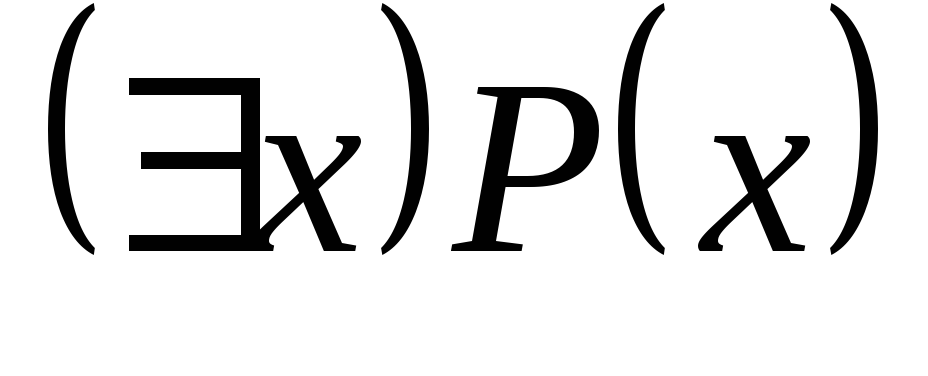 «Существует
х, такое
что
«Существует
х, такое
что 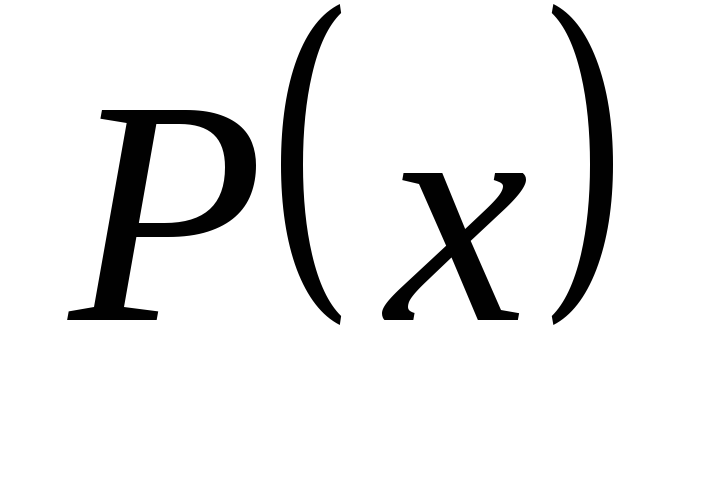 »
или «Для некоторых
х верно
»
или «Для некоторых
х верно
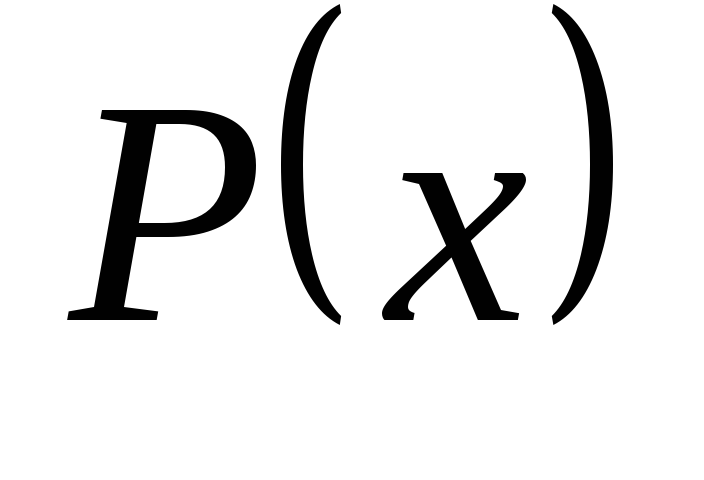 »
или «Хотя бы один х
»
или «Хотя бы один х
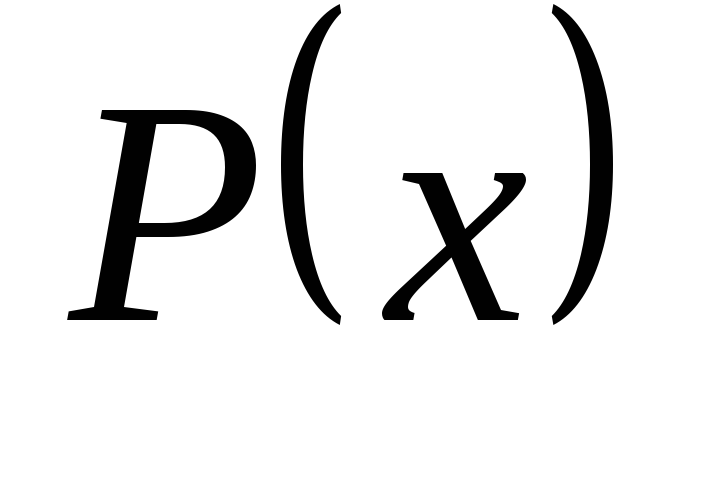 ».
».
Например:
Пусть ![]() :
«Официант х
обслуживает стол
у».
Тогда
:
«Официант х
обслуживает стол
у».
Тогда
![]() означает
«У
любого официанта есть стол, который он
обслуживает».
означает
«У
любого официанта есть стол, который он
обслуживает».
![]() означает
«Каждый
официант обслуживает все столы».
означает
«Каждый
официант обслуживает все столы».
![]() означает
«Существует
стол, который обслуживается некоторым
официантом».
означает
«Существует
стол, который обслуживается некоторым
официантом».
Для
любого предиката ![]() имеют место следующие равносильности:
имеют место следующие равносильности:
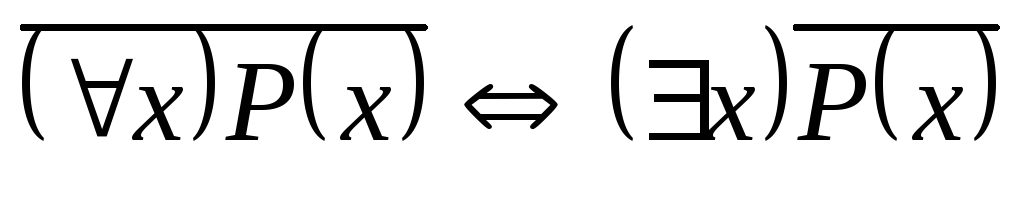 ;
;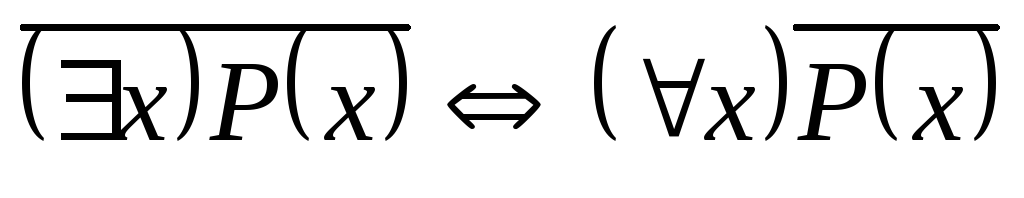 .
.
Эти правила используются для построения отрицаний предложений.
Например:
Постройте отрицание предложения «Некоторые студенты нашего факультета не сдали сессию».
Решение: Р(х):
«Студент х
нашего факультета не сдал сессию».
Тогда исходное предложение запишется
как ![]() ,
а его отрицание как
,
а его отрицание как
![]() ,
что читается как «Все студенты нашего
факультета сдали сессию».
,
что читается как «Все студенты нашего
факультета сдали сессию».
