Билет 18 (цс)

1. Понятие о циклической (круговой) свертке.

2. Связь круговой свертки и ДПФ.

3. Использование циклической свертки для вычисления линейной свертки.

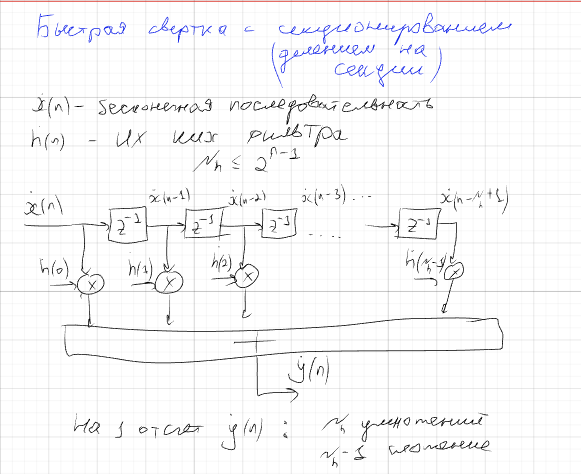
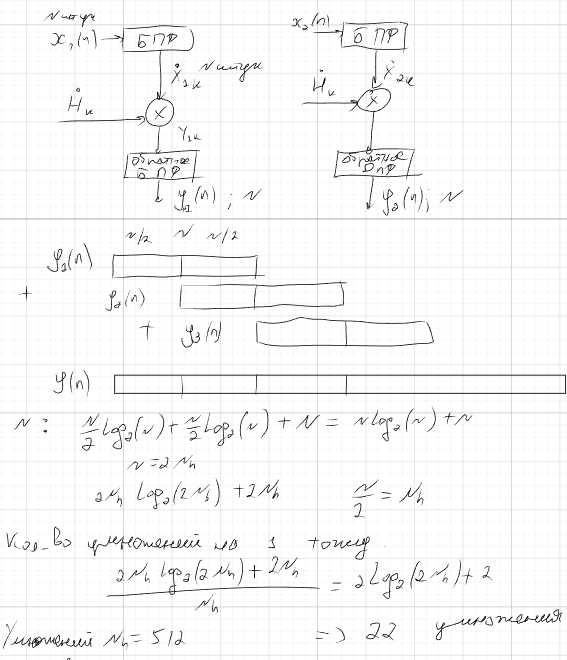
4. Быстрая свертка через БПФ. Примеры

1. Понятие о циклической (круговой) свертке и 2. Связь круговой свертки и ДПФ.

2. Использование циклической свертки для вычисления линейной свертки.

3. Быстрая свертка через БПФ. Примеры

Билет 19 (ких л-фчх)

1. Этапы проектирования цифровых фильтров.

2. Требования к АЧХ, предъявляемые при синтезе фильтров.

3. КИХ-фильтры с линейной ФЧХ, свойства.

4. Порядок фильтра и длина импульсной характеристики.

5. Проектирование КИХ-фильтров методом окон.

6. Эффект Гиббса и назначение окон (на примере окна Кайзера).

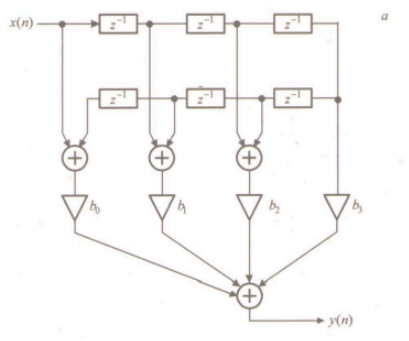
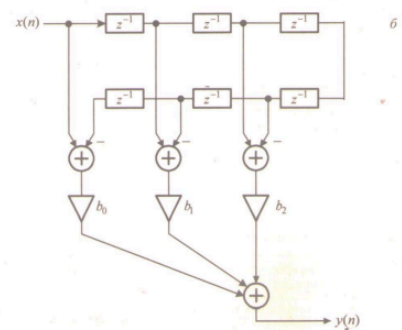
7. Структуры КИХ-фильтров с симметричной и антисимметричной импульсной характеристикой

1. Этапы проектирования цифровых фильтров.

2. Требования к АЧХ, предъявляемые при синтезе фильтров.

ФНЧ ФВЧ

ПФ РФ

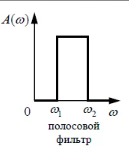
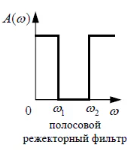
3. КИХ-фильтры с линейной ФЧХ, свойства.

Последовательность {h(n)}, имеет z-преобразование

H(z) = 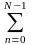h(n) z^-n = b(n) z^-n

Преобразование Фурье от {h(n)}

H(e^j) = h(n) e^–jnT= b(n) e^–jnT

Требование линейности фазовой характеристики означает

 () = –() –    ,

 – постоянная фазовая задержка, выраженная через число интервалов дискретизации n

h(n) = h(N – 1 – n)

h(n) = –h(N – 1 – n)

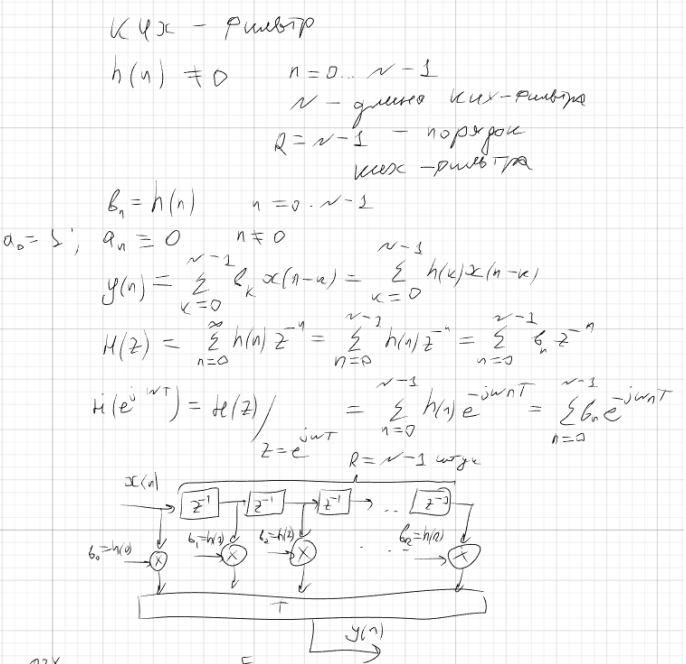
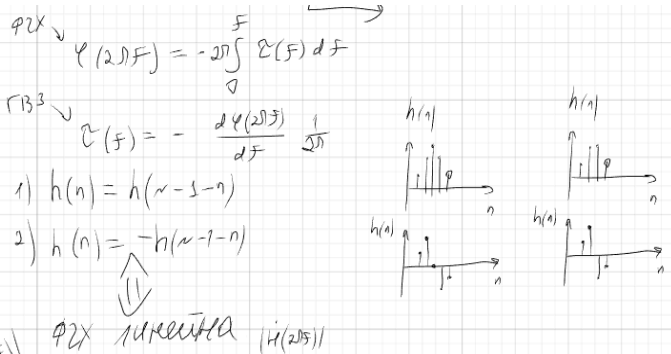
4. Порядок фильтра и длина импульсной характеристики.

R=N-1, N – длина ких фильтра

5. Проектирование КИХ-фильтров методом окон.

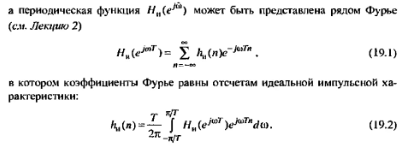
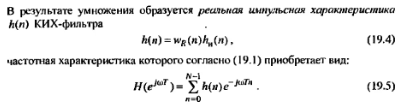
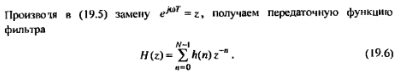
6. Эффект Гиббса и назначение окон (на примере окна Кайзера).

Эффект Гиббса — явление, проявляющиеся при использовании идеальных или резких фильтров. Он характеризуется появлением осцилляций. Это происходит из-за того, что ИФ обладают бесконечной разрешающей способностью и мгновенно обрезают частоты выше или ниже определенной частоты среза. Для смягчения эффекта часто используются увеличение порядка фильтра, применение методов оптимизации параметров фильтрации, выбор более подходящих оконных функций и другие подходы.

7. Структуры КИХ-фильтров с симметричной и антисимметричной импульсной характеристикой

Билет 20 (бих б-z)

1. Этапы проектирования цифровых фильтров.

2. Требования к АЧХ, предъявляемые при синтезе фильтров.

3. Проектирование БИХ-фильтров методом билинейного z-преобразования.

4. Связь порядка фильтра с числом биквадратных звеньев.

5. Нелинейное искажение оси частот при билинейном Z-преобразовании

1. Этапы проектирования цифровых фильтров.

2. Требования к АЧХ, предъявляемые при синтезе фильтров.

ФНЧ ФВЧ

ПФ РФ

3. Проектирование БИХ-фильтров методом билинейного z-преобразования.

при ФВЧ , а потом уже

4. Связь порядка фильтра с числом биквадратных звеньев.