Билет 10 (лдс, чх)
Линейные дискретные системы (ЛДС) с постоянными параметрами.
Частотная характеристика линейной дискретной системы и ее связь с передаточной функцией ЛДС.
Амплитудно- и фазочастотная характеристики ЛДС.
Связь нулей и полюсов передаточной функции с положениями локальных минимумов и максимумов амплитудно-частотной характеристики на частотной оси
Линейные дискретные системы (ЛДС) с постоянными параметрами.
Устойчивые |
Неустойчивые |
|X(n)| < ; |Y(n)| < |X(n)| < ; |Y(n)|
Σ|h(n)| < Σ|h(n)|
h(n) = (по графику) h(n) = (по графику)
Физ. реализуемые |
Физ. нереализуемые |
не нарушает принцип причинности y(n) не опережает x(n)
Частотная характеристика линейной дискретной системы и ее связь с передаточной функцией ЛДС.
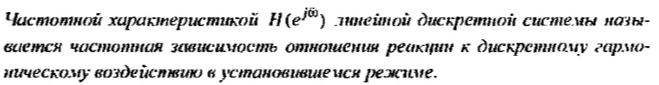
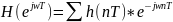– частотная
характеристика лдс
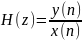
z=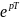
p=jw+o, o=0
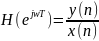
Амплитудно- и фазочастотная характеристики ЛДС.
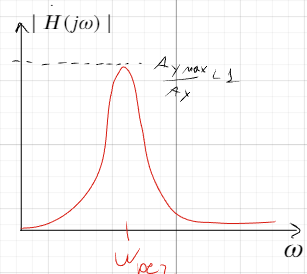
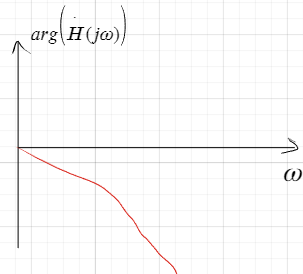
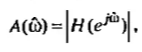
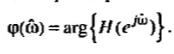
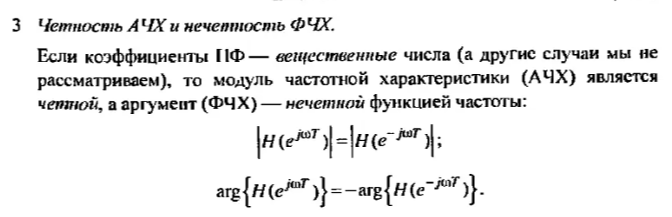
Связь нулей и полюсов передаточной функции с положениями локальных минимумов и максимумов амплитудно-частотной характеристики на частотной оси
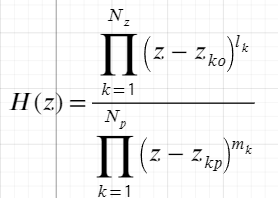
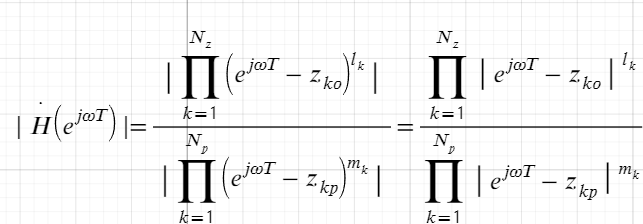
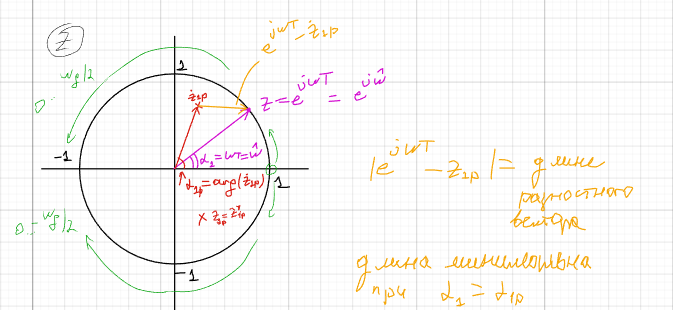
Нули ПФ соответствуют точкам, где АЧХ пересекает ось нулей. Если 0 в левой полуплоскости, то в этой точке локальный min
Полюсы ПФ соответствуют точкам, где АЧХ пересекает ось -180градусов. Если полюс в левой полуплоскости, то в этой точке локальный max
АЧХ дает информацию как система реагирует на различ. f входного сигнала. Положение 0 и полюсов определяет форму этой хар-ки
Билет 11 (ан.Сиг в чо)
Представление аналоговых сигналов в частотной области: спектр периодических сигналов и спектральная плотность апериодических сигналов.
Их связь, физический смысл и размерность.
Свойства интегрального преобразования Фурье (линейность, сдвиг во временной области, сдвиг в частотной области, преобразование произведения сигналов, преобразование свертки сигналов)
Представление аналоговых сигналов в частотной области: спектр периодических сигналов и спектральная плотность апериодических сигналов.
Периодические сигналы могут быть разложены на гармонические компоненты различных частот и амплитуд (разложение Фурье). Главная f определяет основную частоту сигнала, а гармоники кратные этой f
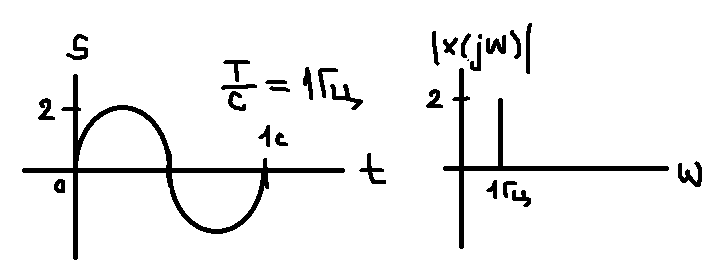
(спектр периодического сигнала)
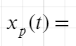
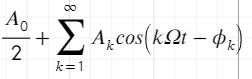
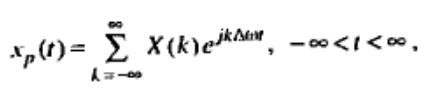
X(jw) – спектр сигнала периодичных сигналов в частотной области
.
(спектр апериодического сигнала)
X(jw) – спектр сигнала апериодичных сигналов в частотной области
Их связь, физический смысл и размерность.
Связь в том, что СПС является особой формой СПАС при условии, что сигнал продолжается бесконечно во времени и представляют информацию о распределении энергии сигнала по различным частотам
Физический смысл спектра периодического сигнала(СПС) заключается в том, что он показывает, какие частоты присутствуют в периодическом сигнале и с какой амплитудой [в, а]
Физический смысл спектральной плотности апериодического сигнала(СПАС) заключается в том, что она показывает, сколько энергии содержится в сигнале в каждом интервале частот. [вт/гц]