Билет 14 (дпф)

1. Дискретное преобразование Фурье (ДПФ) периодических последовательностей.

2. Связь коэффициентов ДПФ периодической последовательности со спектральной плотностью конечной последовательности.

3. Свойства ДПФ (линейность, периодичность, симметрия, сдвиг во временной области, сдвиг в частотной области, преобразование произведения последовательностей, преобразование циклической свертки последовательностей), примеры

1. Дискретное преобразование Фурье (дпф) периодических последовательностей

Дискретное преобразование Фурье (ДПФ) - это метод анализа частотного состава дискретных последовательностей. При применении к периодическим последовательностям, ДПФ может быть использовано для анализа их спектрального содержания

Обратное преобразование Фурье

Но вообще 1\2N потому что в конечном итоге на графиках мы получим амплитуду в 2 раза меньше, а фазу на 90 градусов меньше, т.е 1 -> 0.5; , 0 -> -90

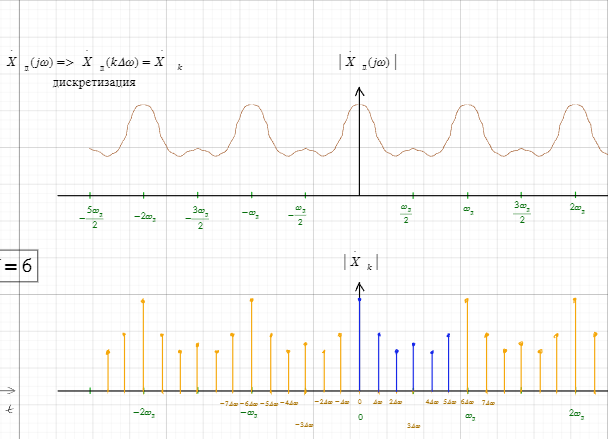
2. Связь коэффициентов дпф периодической последовательности со спектральной плотностью конечной последовательности

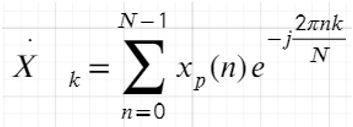
3. Свойства ДПФ (линейность, периодичность, симметрия, сдвиг во временной области, сдвиг в частотной области, преобразование произведения последовательностей, преобразо вание циклической свертки последовательностей), примеры

Билет 15 (бпф t)

1. Быстрое преобразование Фурье (БПФ) с прореживанием по времени для размера блока N = 2^r.

2. Понятие о поворачивающем множителе.

3. Понятие о графе «бабочка» для БПФ с прореживанием по времени, алгоритм его работы.

4. Пример структуры модуля БПФ на основе 8-точечного БПФ.

5. Понятие о бит-реверсной перестановке элементов последовательности

1. Быстрое преобразование Фурье (БПФ) с прореживанием по времени для размера блока N=2^r.

В БПФ по времени последовательность разбивается на две подпоследовательности: четные и нечетные отсчеты.

Далее применяется рекурсивное разделение и объединение этих под последовательностей, что приводит к сокращению количества операций.

Этот метод обычно используется, когда входная последовательность уже является временной последовательностью.

Этот метод обычно используется для оптимизации вычислений в ситуациях, когда длина последовательности является степенью двойки

2. Понятие о поворачивающем множителе.

Поворачивающий множитель — комплексное число, использующиеся в БПФ для реализации преобразования

Он вводится для учета различных частотных компонент в преобразовании и обеспечивает вращение в пространстве комплексных чисел, что позволяет учитывать фазовую информацию и обеспечивает корректное преобразование различных частот.

Его использование позволяет уменьшить количество операций

3. Понятие о графе «бабочка» для БПФ с прореживанием по времени, алгоритм его работы.

Исходная последовательность разбивается на две подпоследовательности: четные и нечетные отсчеты. Это делается путем разделения последовательности на две части, где элементы с четными индексами идут в одну подпоследовательность, а элементы с нечетными индексами - в другую

Выполняется операция, которая сочетает их вместе для получения результата БПФ. Обычно эта операция включает в себя умножение одного элемента на поворачивающий множитель и добавление к другому элементу, что приводит к формированию двух элементов результата

Результаты комбинируются в итоговый результат БПФ

4. Пример структуры модуля БПФ на основе 8-точечного БПФ.