Понятие о бит-реверсной перестановке элементов последовательности
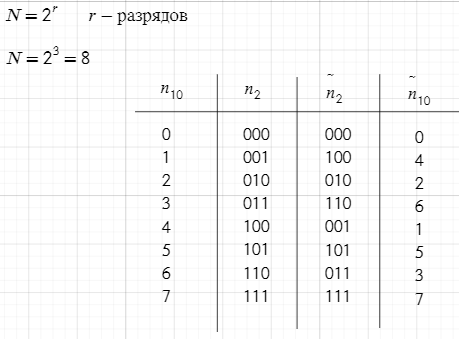
Бит-реверсная перестановка преобразует индексы элементов последовательности, инвертируя порядок бит в их двоичном представлении
Билет 16 (бпф f)
Быстрое преобразование Фурье (БПФ) с прореживанием по частоте для размера блока N = 2r.
Понятие о поворачивающем множителе.
Понятие о графе «бабочка» для БПФ с прореживанием по частоте, алгоритм его работы.
Пример структуры модуля БПФ на основе 8-точечного БПФ.
Понятие о бит-реверсной перестановке элементов последовательности
Быстрое преобразование Фурье (БПФ) с прореживанием по частоте для размера блока N = 2r.
В БПФ по частоте преобразование Фурье вычисляется непосредственно в частотной области, без разделения последовательности.
Этот метод основан на формуле обратного преобразования Фурье и обычно применяется, когда входная последовательность уже является спектром в частотной области.
Понятие о поворачивающем множителе.
Поворачивающий множитель — комплексное число, использующиеся в БПФ для реализации преобразования
Он вводится для учета различных частотных компонент в преобразовании и обеспечивает вращение в пространстве комплексных чисел, что позволяет учитывать фазовую информацию и обеспечивает корректное преобразование различных частот.
Его использование позволяет уменьшить количество операций
Понятие о графе «бабочка» для БПФ с прореживанием по частоте, алгоритм его работы.
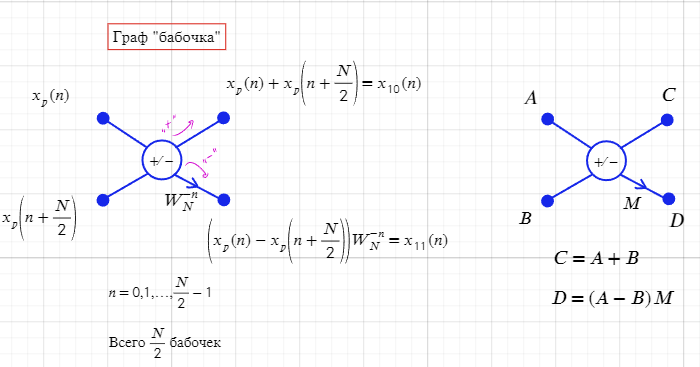
Исходная последовательность разбивается на две подпоследовательности: четные и нечетные отсчеты. Это делается путем разделения последовательности на две части, где элементы с четными индексами идут в одну подпоследовательность, а элементы с нечетными индексами - в другую
Выполняется операция, которая сочетает их вместе для получения результата БПФ. Обычно эта операция включает в себя умножение одного элемента на поворачивающий множитель и добавление к другому элементу, что приводит к формированию двух элементов результата
Результаты комбинируются в итоговый результат БПФ
Пример структуры модуля БПФ на основе 8-точечного БПФ.
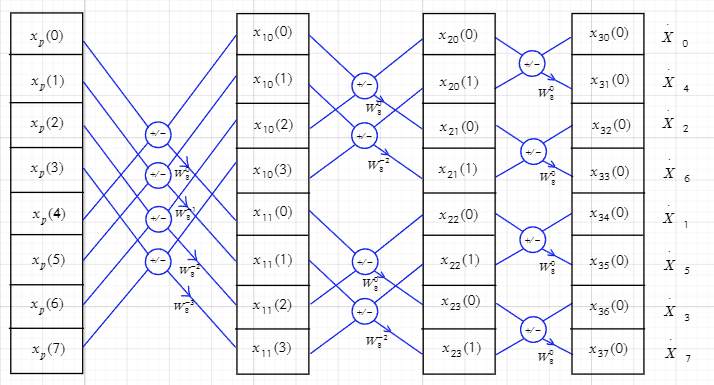
Понятие о бит-реверсной перестановке элементов последовательности
Бит-реверсная перестановка преобразует индексы элементов последовательности, инвертируя порядок бит в их двоичном представлении
Билет 17 (ис)
Интеграл свертки.
Связь интеграла свертки с образами по Лапласу и Фурье сворачиваемых сигналов.
Линейная дискретная свертка.
Связь дискретной свертки с Фурье- и Z-образами последовательностей.
Использование для вычисления реакции линейной цепи с постоянными параметрами. Примеры
Интеграл свертки и 2. Связь интеграла свертки с образами по Лапласу и Фурье сворачиваемых сигналов.
Линейная дискретная свертка и 3. Связь дискретной свертки с Фурье- и Z-образами последовательностей.
Использование для вычисления реакции линейной цепи с постоянными параметрами. Примеры
