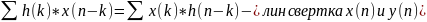Билет 3 (мат модель ацп)
Математическая модель АЦП как идеального амплитудно-импульсного модулятора.
Математическая модель дискретизированного во времени сигнала.
Преобразование Лапласа и Фурье дискретизированного во времени сигнала.
Интервал/период дискретизации, частота и угловая частота дискретизации.
Математическая модель АЦП как идеального амплитудно-импульсного модулятора.
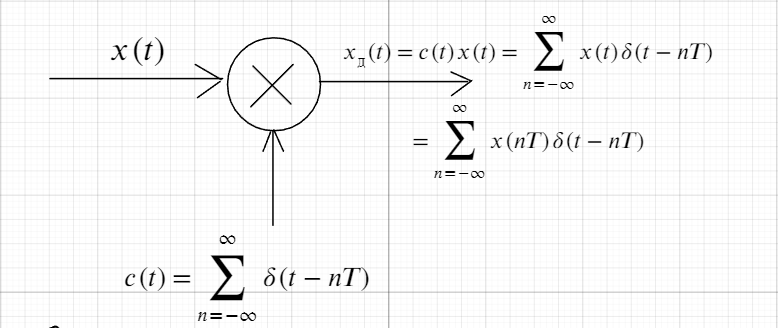
Математическая модель дискретизированного во времени сигнала.
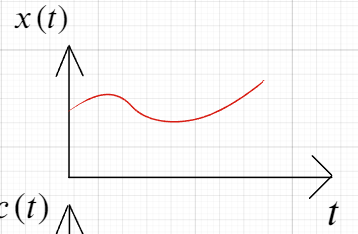
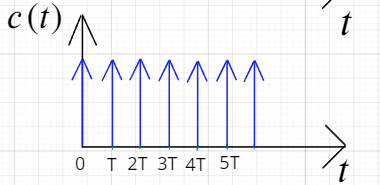
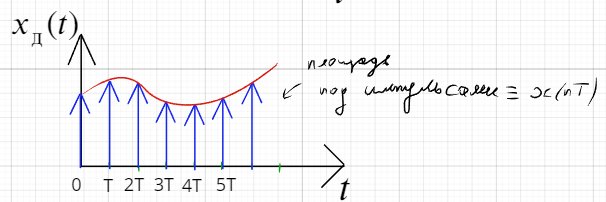
Преобразование Фурье и Лапласа дискретизированного во времени сигнала
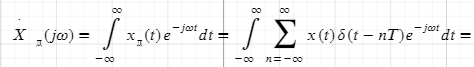
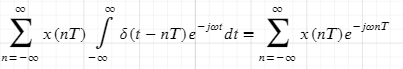
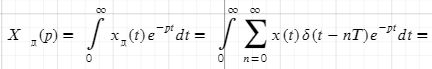
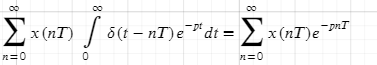
Интервал/период дискретизации, частота и угловая частота дискретизации.
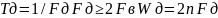
Билет 4 (z c лапласом)
Связь прямого Z-преобразования с дискретным преобразованием Лапласа.
Отображение P-плоскости в Z-плоскость.
Преобразование начала координат, оси частот, левой и правой полуплоскостей из P-плоскости в Z-плоскость.
Неоднозначность преобразования P-плоскости в Z-плоскость (наложение множества точек на прямой из P-плоскости в одну точку Z-плоскости).
Связь прямого Z-преобразования с дискретным преобразованием Лапласа.
Z =
Отображение P-плоскости в Z-плоскость.
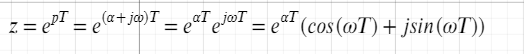
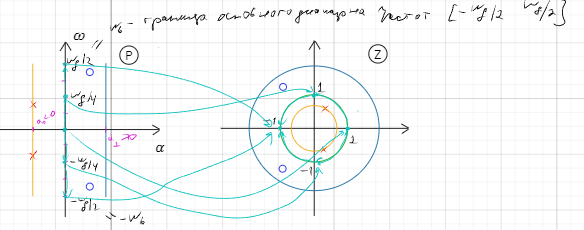
Преобразование начала координат, оси частот, левой и правой полуплоскостей из P-плоскости в Z-плоскость.
Неоднозначность преобразования P-плоскости в Z-плоскость (наложение множества точек на прямой из P-плоскости в одну точку Z-плоскости).
Z = создает неоднозначность, поскольку несколько точек в P плоскости могут быть отображены в одну точку Z плоскости, происходит из за периодичности exp функции
Билет 5 (обратное z)
Обратное Z-преобразование.
Вычисление обратного z-преобразования с помощью вычетов.
Формулы для вычисления вычетов в простых и кратных полюсах.
Пример вычисления обратного z-преобразования
Обратное Z-преобразование
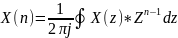
Г – замкнутый контур, охватывающий начало координат плоскости Z и все полюсы подинтеграл. выражения
Вычисление обратного z-преобразования с помощью вычетов
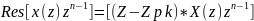
Zкр- особая точка в k полюсе
Формулы для вычисления вычетов в простых и кратных полюсах
Простые полюса
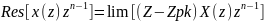
Кратные полюса
Пример вычисления обратного z-преобразования
X(z)
=
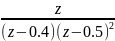[z1p
= 0.4 m1=1] [z2p=0.5 m2=2]
Y(n)
=
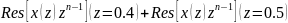
Z=0.4 m=1
=
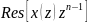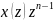[(z-0.4)
]
=(z-0.4)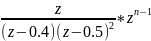
=
=
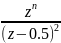Z=0.5 m=2
=
[
]
=
=
=
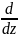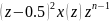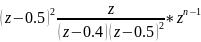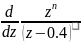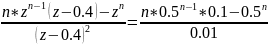
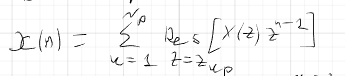
Y(n)
=
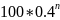+ 100[
]
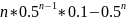Билет 6 (ру)
Разностные уравнения.
Решение разностных уравнений с помощью Z-преобразования.
Пример решения разностных уравнений с помощью Z-преобразования.
Разностные уравнения.
Воздействие x(n) и реакцию y(n) можно описать разностным уравнением
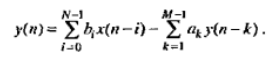
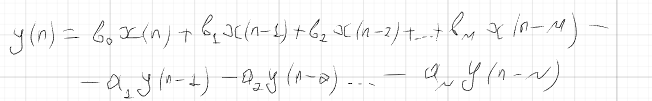
Решение разностных уравнений с помощью Z-преобразования
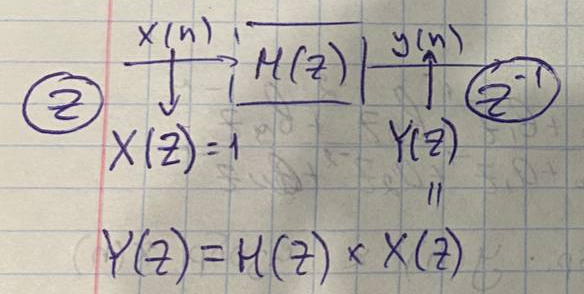
Пример решения разностных уравнений с помощью Z-преобразования
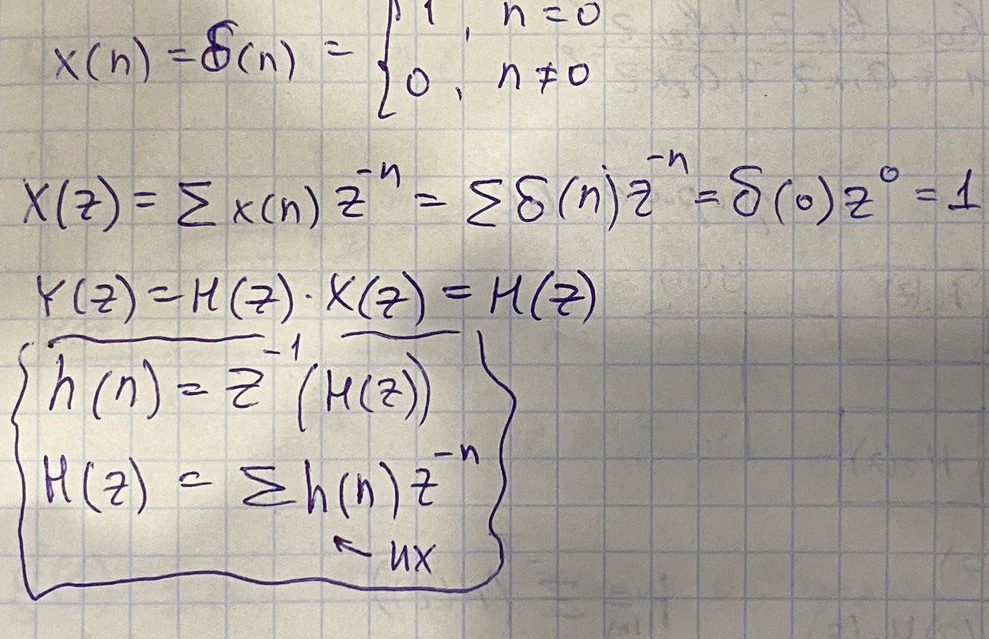
Билет 7 (лдс, св-ва)
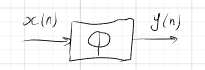
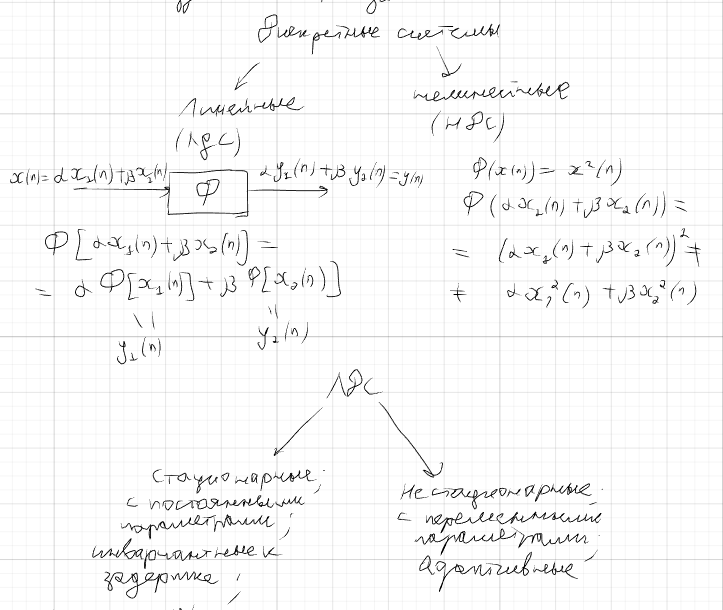
Линейные дискретные системы (ЛДС) с постоянными параметрами.
Основные свойства (линейность, инвариантность к сдвигу во времени, физическая реализуемость), формулировка, примеры.
Понятие об импульсной характеристике ЛДС.
Вычисление реакции ЛДС через импульсную характеристику.
Определение устойчивости ЛДС.
Требования к импульсной характеристике для устойчивых ЛДС.
Линейные дискретные системы (ЛДС) с постоянными параметрами.
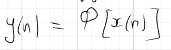
Устойчивые |
Неустойчивые |
|X(n)|
<
; |Y(n)|
<
|X(n)|
<
; |Y(n)|
Σ|h(n)| < Σ|h(n)|
h(n)
=
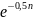(по графику) h(n)
=
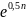(по графику)
Физ. реализуемые |
Физ. нереализуемые |
не нарушает принцип причинности y(n) не опережает x(n)
Основные свойства (линейность, инвариантность к сдвигу во времени, физическая реализуемость), формулировка, примеры.
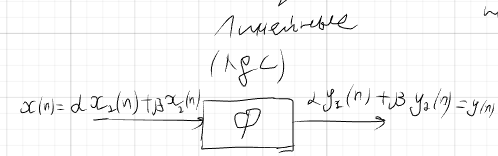
Задержка x(n) приводит к задержке y(n) на то же время
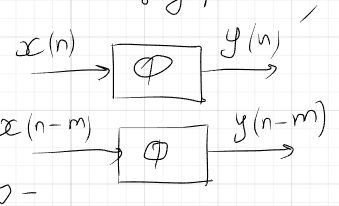
Свойство памяти, устойчивость
Понятие об импульсной характеристике ЛДС.
h[n] = {1, 0.5, 0.25} подадим дельта импульс x[n] = {1, 0, 0}, то на выходе
y[n] = {1, 0.5, 0.25, 0, 0} где каждое значение выходного сигнала представляет собой свертку входного сигнала и импульсной характеристики в соответствующих моментах времени.
Вычисление реакции ЛДС через импульсную характеристику.
Y(n)
=
