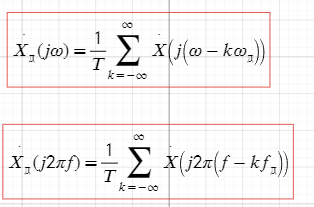- •Билет 1 (сигналы)
- •Процесс дискретизации, пример
- •Понятие интервала дискретизации, понятие частоты дискретизации, угловой частоты дискретизации и их связь
- •Процесс квантования и преобразования отсчетов в двоичный код, пример
- •Билет 2 (прямое z)
- •Билет 3 (мат модель ацп)
- •Билет 4 (z c лапласом)
- •Билет 5 (обратное z)
- •Билет 6 (ру)
- •Билет 7 (лдс, св-ва)
- •Требования к импульсной характеристике для устойчивых лдс.
- •Билет 8 (лдс, ру)
- •Билет 9 (лдс, пф)
- •Билет 10 (лдс, чх)
- •Билет 11 (ан.Сиг в чо)
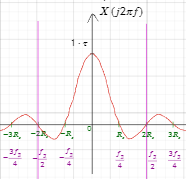
- •X(jw) – спектр сигнала периодичных сигналов в частотной области
- •X(jw) – спектр сигнала апериодичных сигналов в частотной области
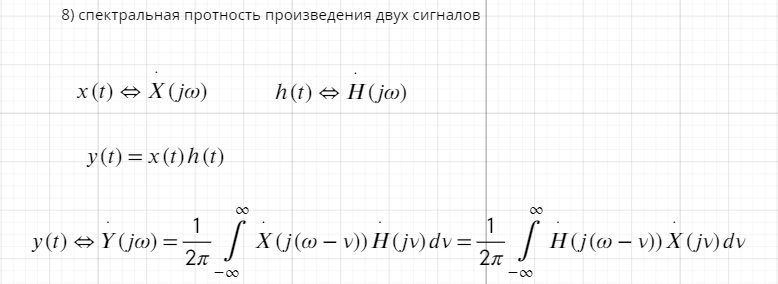
- •Свойства интегрального преобразования Фурье (линейность, сдвиг во временной области, сдвиг в частотной области, преобразование произведения сигналов, преобразование свертки сигналов
- •Билет 12 (сп нс)
- •Билет 13 (т.Котельникова)
- •Билет 14 (дпф)
- •Дискретное преобразование Фурье (дпф) периодических последовательностей
- •Связь коэффициентов дпф периодической последовательности со спектральной плотностью конечной последовательности
- •Билет 15 (бпф t)
- •Понятие о бит-реверсной перестановке элементов последовательности
- •Билет 16 (бпф f)
- •Билет 17 (ис)
- •Билет 18 (цс)
- •Билет 19 (ких л-фчх)
- •Билет 20 (бих б-z)
- •Нелинейное искажение оси частот при билинейном z-преобразовании
- •Билет 21 (бих иИх)
- •Этапы проектирования цифровых фильтров
- •Наложение копий частотной характеристики фильтра при преобразовании
Свойства интегрального преобразования Фурье (линейность, сдвиг во временной области, сдвиг в частотной области, преобразование произведения сигналов, преобразование свертки сигналов

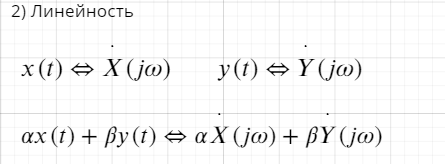


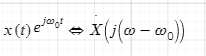



Билет 12 (сп нс)
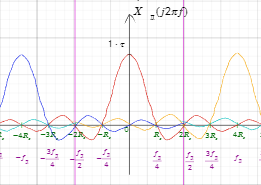
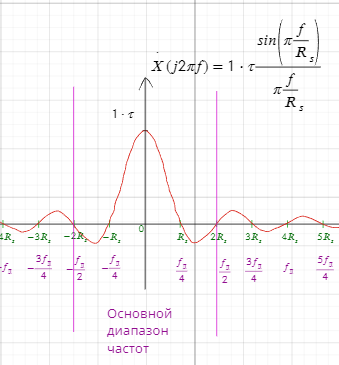
Спектральная плотность непрерывного сигнала до и после дискретизации, и их связь.
Спектральная плотность сигнала после дискретизации при условии удовлетворения или не удовлетворения условий теоремы Котельникова.
Явление наложения спектров при дискретизации непрерывных сигналов.
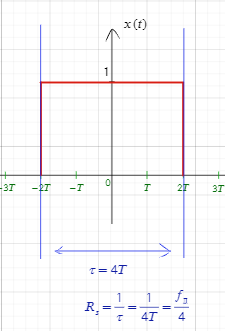
Примеры
Спектральная плотность непрерывного сигнала до и после дискретизации, и их связь.
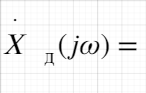
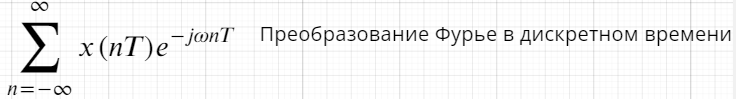
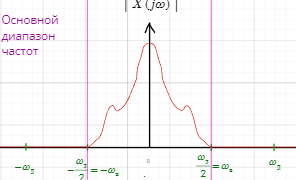
Связь между непрерывной спектральной плотностью и спектральной плотностью после дискретизации заключается в том, что последняя представляет собой аппроксимацию первой в дискретной форме, т.е. является приближенной оценкой спектральной плотности непрерывного сигнала в этом ограниченном частотном диапазоне.
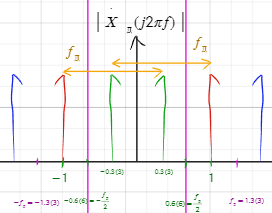
Спектральная плотность сигнала после дискретизации при условии удовлетворения или не удовлетворения условий теоремы Котельникова.
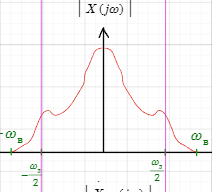
Условия т.Котельникова выполняются(Fd>=2Fv)
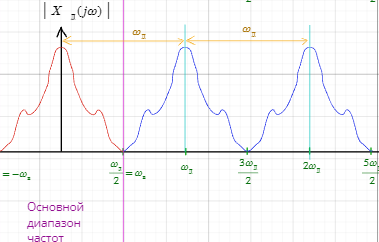

Условия т.Котельникова не выполняются(Fd<2Fv)
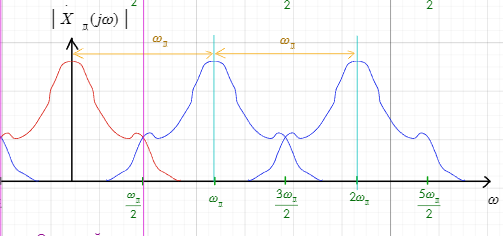


Явление наложения спектров при дискретизации непрерывных сигналов.

Примеры
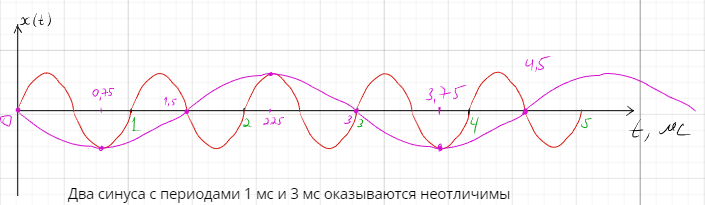
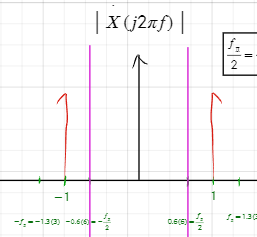
Билет 13 (т.Котельникова)
Теорема отсчетов Котельникова во временной области, формулировка.
Импульсная характеристика восстанавливающего фильтра, ее свойства.
Процесс восстановления наглядно графически, примеры.
Интерпретация процесса восстановления непрерывного сигнала в частотной области как идеальная низкочастотная фильтрация дискретизированного во времени сигнала
Теорема отсчетов Котельникова во временной области, формулировка.

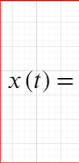
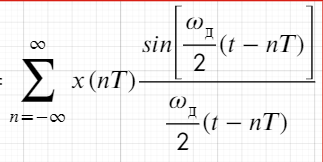
Импульсная характеристика восстанавливающего фильтра, ее свойства.
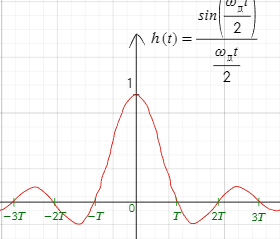
Свойства линейности и временной инвариантности
Означает, что его импульсная характеристика остается неизменной во времени и что фильтр ведет себя линейно
Процесс восстановления наглядно графически, примеры.
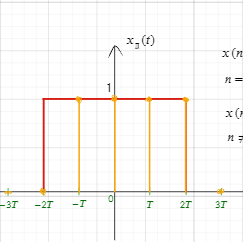
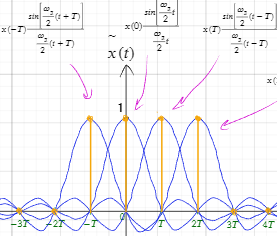
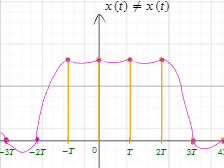
Интерпретация процесса восстановления непрерывного сигнала в частотной область как идеальная низкочастотная фильтрация дискретизированного во времени сигнала
При дискретизации сигнала происходит потеря информации о высокочастотных компонентах. Для восстановления требуется применить фильтр, который подавит эти высокочастотные компоненты.
ИФНЧ подавляет все частоты, превышающие 1\2Fd, сохраняя только компоненты сигнала с частотами ниже этого порога.
В частотной области это означает, что все частоты выше частоты Найквиста будут подавлены, а частоты ниже этого порога будут сохранены. Это приводит к формированию частотного спектра, который соответствует спектру непрерывного сигнала до его дискретизации, но с ограничением по частоте.
Восстановление сигнала: Применение идеальной низкочастотной фильтрации в частотной области к дискретизированному сигналу позволяет удалить искажения, вызванные процессом дискретизации, и восстановить аналоговый сигнал во временной области.