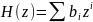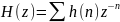Требования к импульсной характеристике для устойчивых лдс.
Достаточно, чтобы выполнялось условие абсолютной сходимости ряда Σ|h(n)| <
КИХ системы устойчивы
Билет 8 (лдс, ру)
Линейные дискретные системы (ЛДС) с постоянными параметрами.
Понятие о разностном уравнении. Порядок разностного уравнения.
Связь разностного уравнения и структуры ЛДС, пример.
Рекурсивные и нерекурсивные ЛДС, структурные схемы.
Понятие КИХ и БИХ систем.
Связь КИХ и БИХ систем с рекурсивными и нерекурсивными системами.
Устойчивость КИХ и БИХ систем.
Линейные дискретные системы (ЛДС) с постоянными параметрами.
Устойчивые |
Неустойчивые |
|X(n)| < ; |Y(n)| < |X(n)| < ; |Y(n)|
Σ|h(n)| < Σ|h(n)|
h(n) = (по графику) h(n) = (по графику)
Физ. реализуемые |
Физ. нереализуемые |
не нарушает принцип причинности y(n) не опережает x(n)
Понятие о разностном уравнении. Порядок разностного уравнения.
Порядок max(N,M)
Связь разностного уравнения и структуры ЛДС, пример.
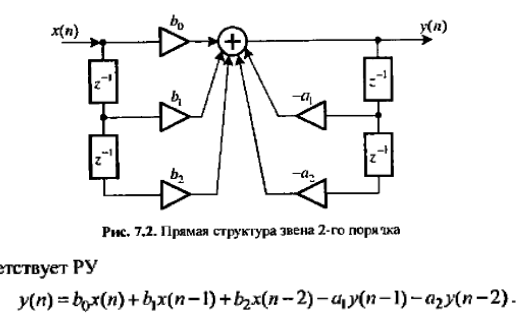
Рекурсивные и нерекурсивные ЛДС, структурные схемы.
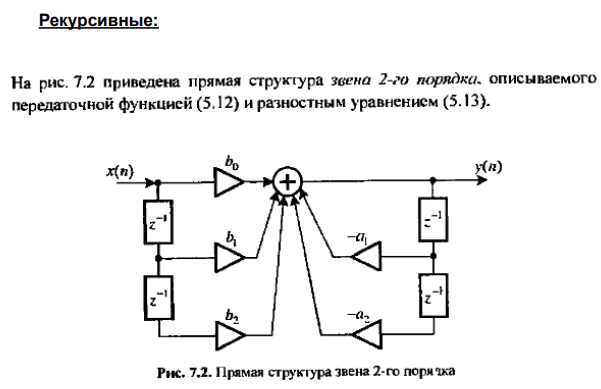
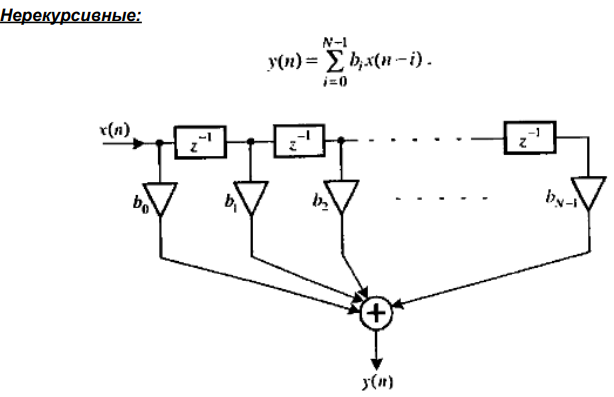
Понятие КИХ и БИХ систем.
Понятия КИХ и БИХ систем связаны с характером их ИХ
В КИХ системах ИХ имеет конечную длину. В БИХ системах ИХ имеет бесконечную длину.
Связь КИХ и БИХ систем с рекурсивными и нерекурсивными системами.
КИХ – не рекурсивная (нет ОС) БИХ – рекурсивная (есть ОС)
Устойчивость КИХ и БИХ систем
КИХ устойчив, БИХ нет (но да, если все |полюса| < 1)
Билет 9 (лдс, пф)
Линейные дискретные системы (ЛДС) с постоянными параметрами.
Понятие о передаточной функции ЛДС.
Связь передаточной функции ЛДС с ее структурой, примеры.
Нули и полюса передаточной функции линейной дискретной системы, определение.
Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции.
Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия.
Линейные дискретные системы (ЛДС) с постоянными параметрами.
Устойчивые |
Неустойчивые |
|X(n)| < ; |Y(n)| < |X(n)| < ; |Y(n)|
Σ|h(n)| < Σ|h(n)|
h(n) = (по графику) h(n) = (по графику)
Физ. реализуемые |
Физ. нереализуемые |
не нарушает принцип причинности y(n) не опережает x(n)
Понятие о передаточной функции ЛДС.
Передаточная функция ЛДС — это математическая функция, которая описывает взаимосвязь между входным и выходным сигналами системы в частотной области. Она представляет собой отношение преобразования Лапласа (или преобразования Z для дискретных систем) выходного сигнала к входному сигналу при нулевых начальных условиях.
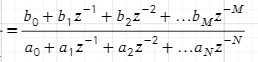
Связь передаточной функции ЛДС с ее структурой, примеры.
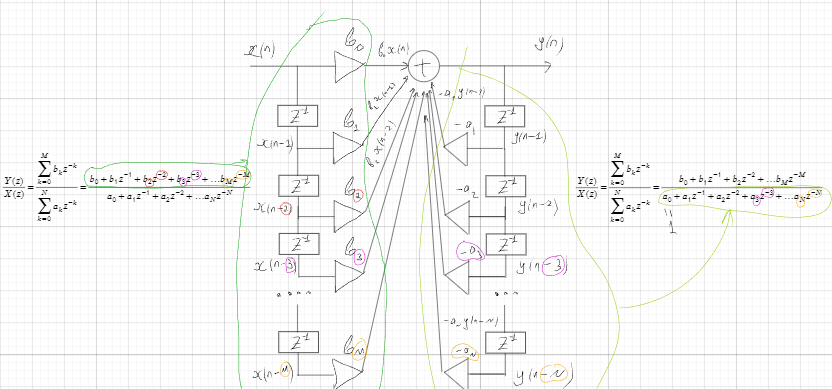
Нули и полюса передаточной функции линейной дискретной системы, определение.
НУЛИ = корни уравнения числителя
ПОЛЮСА = значения z, при которых знаменатель ПФ равен 0
Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции.
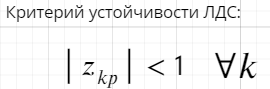
Все полюса ее ПФ находились внутри окружности единичного радиуса Zпл
Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия
РЕК НЕРЕК
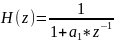если
b0=1
