Оглавление

БИЛЕТ 1 (сигналы) 2

БИЛЕТ 2 (прямое z) 4

БИЛЕТ 3 (мат модель АЦП) 5

БИЛЕТ 4 (z c лапласом) 6

БИЛЕТ 5 (обратное z) 7

БИЛЕТ 6 (РУ) 8

БИЛЕТ 7 (ЛДС, СВ-ВА) 9

БИЛЕТ 8 (ЛДС, РУ) 11

БИЛЕТ 9 (ЛДС, ПФ) 14

БИЛЕТ 10 (ЛДС, ЧХ) 16

БИЛЕТ 11 (АН.СИГ в ЧО) 19

БИЛЕТ 12 (СП НС) 22

БИЛЕТ 13 (Т.КОТЕЛЬНИКОВА) 25

БИЛЕТ 14 (ДПФ) 28

БИЛЕТ 15 (БПФ t) 31

БИЛЕТ 16 (БПФ f) 34

БИЛЕТ 17 (ИС) 37

БИЛЕТ 18 (ЦС) 39

БИЛЕТ 19 (КИХ л-ФЧХ) 43

БИЛЕТ 20 (БИХ Б-Z) 47

БИЛЕТ 21 (БИХ иИХ) 49

Билет 1 (сигналы)

1. Аналоговые, дискретные и цифровые сигналы, определение.

2. Процесс дискретизации, пример.

3. Понятие интервала дискретизации, понятие частоты дискретизации, угловой частоты дискретизации и их связь.

4. Процесс квантования и преобразования отсчетов в двоичный код, пример.

5. Связь количества уровней квантования и разрядности кодовых слов на выходе аналого-цифрового преобразователя, пример.

6. Понятие о нормированной частоте и основном диапазоне частот.

1. Аналоговые, дискретные и цифровые сигналы, определение Аналоговый сигнал – непрерывный во времени и состоянию, описывается непрерывной функцией

Дискретный сигнал – дискретный во времени и непрерывный по состоянию, описывается решетчатой функцией

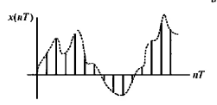
Цифровой сигнал – дискретный во времени и квантованный по состоянию, описывается квантованной решетчатой функцией

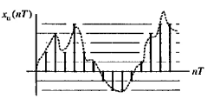
2. Процесс дискретизации, пример

Процесс дискретизации — процесс преобразования непрерывного сигнала в дискретный формат путем выборки значений сигнала на определенных интервалах времени

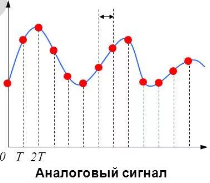
3. Понятие интервала дискретизации, понятие частоты дискретизации, угловой частоты дискретизации и их связь

Интервал дискретизации — это временной или пространственный интервал между соседними дискретными отсчетами сигнала

Частота дискретизации — это количество отсчетов сигнала, сделанных за одну секунду.

Угловая частота дискретизации — это частота дискретизации, выраженная в радианах за секунду

Fd = 1/T w = 2πFd

4. Процесс квантования и преобразования отсчетов в двоичный код, пример

Процесс квантования – процесс, определяющий значения отсчетов сигнала до ближайшего уровня квантования

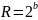кол-во уровней квантования (b – разрядность АЦП)

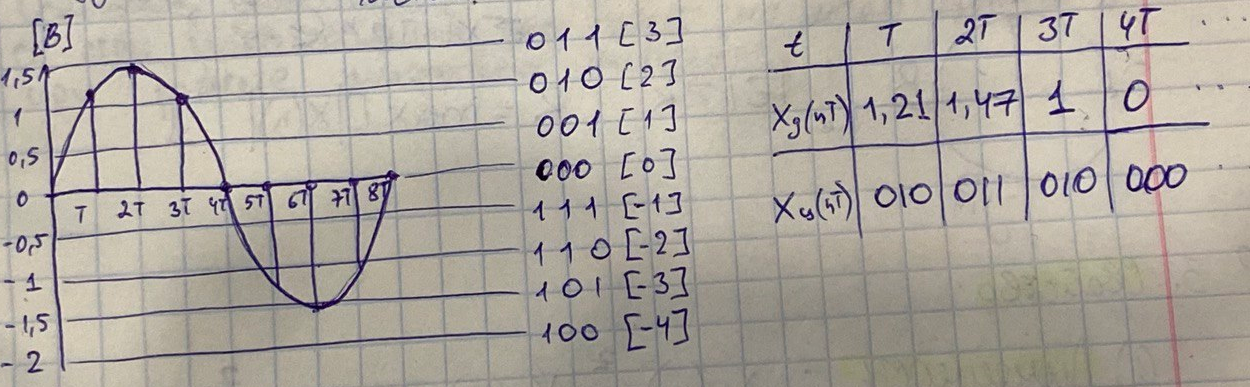
Количество уровней квантования определяет, насколько точно может быть представлен аналоговый сигнал в цифровой форме. Чем больше уровней квантования, тем более точно сигнал может быть представлен в цифровом виде.

если уровней кв. 8, то разрядность кодового слова 3бита. 16->4бита

Нормированной частота - представление частоты в безразмерной форме, что облегчает сравнение частот сигналов в различных контекстах

(Абсолютная частота нормированная к Fd)

Fnorm=f/Fd f – текущая частота

Основной диапазон - [0; Fd/2] по т.Котельникова

Билет 2 (прямое z)

1. Прямое Z – преобразование, определение.

2. Область сходимости, определение, примеры.

3. Свойства (линейность, z-преобразование задержанной копии последовательности, z-преобразование последовательности x(n), умноженной на множитель в форме показательной функции Wn , z-преобразование свертки двух последовательностей).

1. Прямое Z-преобразование – преобразование для перевода последовательности дискретных данных из временной области в частотную область.

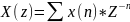
x[n] - входная последовательность дискретных данных

X(z) - Z-преобразование входной последовательности,

z - комплексная переменная

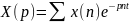– диск. Лаплас Z=

2. Область сходимости – множество точек в комплексной плоскости Z, для которых Z-преобразование сходится и имеет конечное значение, т.е

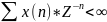
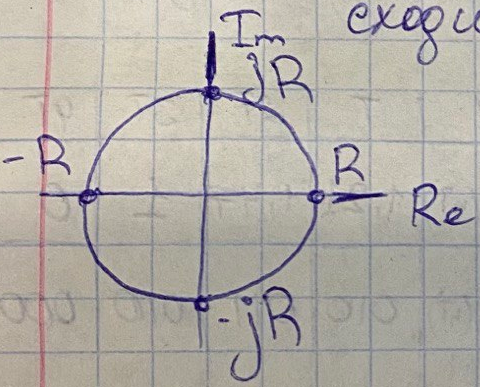
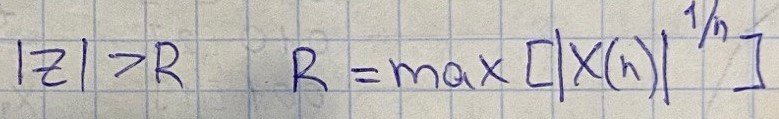
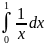Область сходимости этого интеграла - все значения x от 0 до 1.За пределами интеграл расходится.

3. Свойства

Линейность

X1(n) == X1(z) X2(n) == X2(z)

aX1(n)+bX2(n) == aX1(z)+bX2(z)

Теорема о задержке

X(n-m) == X(z)*z^-m

Теорема о свертке

x(n) h(n)

X(z) H(z)

Y(n) =

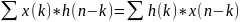
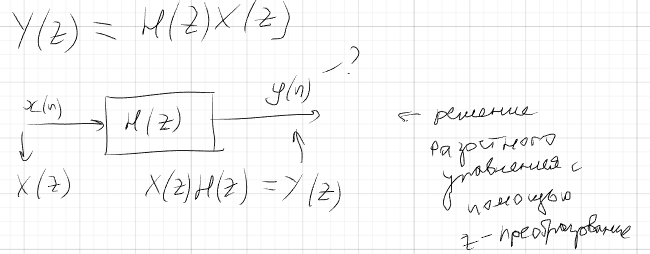
Z изображение * на exp множитель

Y(n) = x(n)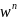 w=const

Y(z) = x(z*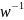 )