854

Функции, предназначенные для решения задач линейной алгебры, собраны в разделе Векторы и матрицы, который открывается через мастера вставки функций, как показано на рисунке 7.21.

Рисунок 7.21. Меню для вставки функций

Рассмотрим наиболее часто используемые функции.

Функции определения матриц и операции с блоками матриц

matrix(m,n,f) – создает и заполняет матрицу размерности m x n, элемент которой, расположенный в i-й строке, j-м столбце, равный значению f(i,j) функции f(x,y).

diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v.

identity(n) – создает единичную матрицу порядка n;

augment(A,B) – формирует матрицу, в первых столбцах которой содержится матрица А, а в последних матрица В( матрицы должны иметь одинаковое число строк).

stack(A,B) – формирует матрицу, в первых строках которой содержится матрица А, а в последних матрица В( матрицы должны иметь одинаковое число столбцов).

submatrix(A,ir,jr,ic,jc) - формирует матрицу, которая является блоком матрицы А, расположенным в строках с ir по jr и в столбцах с ic по jc, ir jr, ic jc.

121

Внимание!!! Номер первой строки(столбца) матрицы или первый компонент вектора хранится в MathCad в переменной, которая пишется прописными буквами: ORIGIN. По умолчанию нумерация начинается с 0 (ORIGIN=0), а в математической записи нумерация должна быть равна 1, по этому всегда должна быть выполнена команда:

ORIGIN:= 1

Определение матриц с помощью функции Matrix:

ORIGIN:= 1 Нумирация строк и столбцов матрицы начинается с 1. Определенная матрица А размерности 3х4, каждый

f(x,y):= x+y элемент которой равен сумме номеров строки и столб-

A:=matrix(3,4,f) ца, в которых он расположен: А={Aij},Aij = i+j

Следует обратить внимание на то, что функция matrix A= игнорирует оператор ORIGIN:= 1 и нумерует строки и столбцы, начиная с 0, Аi,j=0.

Приведем два способа правильного определения матрицы А={Aij},Aij = i+j, с помощью функции matrix.

122

Операции с блоками матриц:

Функции вычисления числовых характеристик матриц

Last (v) = 3 – номер последнего элемента вектора V.

Length(E<1>)=4 – длина (число элементов) первого столбца матрицы Е. Rows(b)=3 cols(b)=7 – число строк и число столбцов матрицы В. Tr(D)=6 – След (сумма диагональных элементов) матрицы D.

Rank(b)=3 –ранг матрицы B.

Max(b)=7 – Наибольший элемент матрицы В.

Функции, реализующие численные алгоритмы решения задач линейной алгебры

Rref(A) – приведение матрицы к ступенчатому виду с единичным базисным минором (выполняет элементарные операции со строками матрицы); Eigenvals(A) – вычисление собственного значения матрицы А; Eigenvecs(A) – вычисление собственных векторов квадратной матрицы А; значением функции является матрица, столбцами которой есть собственные векторы матрицы А, порядок следования которых отвечает порядку следования собственных значений, вычисленных функцией Eigenvals(A); Eigenvec(A, l ) – – вычисление собственного вектора квадратной матрицы

А, отвечающего собственному значению l ;

lsolve(A,b) – решение системы линейных уравнений Ax = b .

123

Задание 1. Решение линейной системы С×х=b с помощью функции lsolve

На рабочем поле введите ORIGIN:= 1

Определите матрицу системы С и правую часть b, на рабочем поле введите:

Для решения системы C×x=b на рабочем поле введите:

1 x:=lsolve(C,b) , введите x = , получите решение х = 2 3

Для проверки правильности решения, на рабочем поле введите матрицу, как показано на рисунке 7.22.

Результат

Проверка правильности результата

Рисунок 7.22. Фрагмент рабочего окна решения системы уравнений через встроенную функцию lsolve

Задание 2. Приведение матрицы к ступенчатому виду

Выполните действия, как показано на рисунке 7.23.

-Расширенная матрица системы Сх=b приведена к ступенчатому виду, т.е. система решина методом Гаусса, последний столбец –

решение системы.

Рисунок 7.23. Приведение матрицы к ступенчатому виду

124

Задание 3. Вычисление собственных значений и собственных векторов матрицы С.

Выполните действия, как показано на рисунке 7.24:

Элементы вектора L- собственные значения матрицы С.

Столбцы матрицы собственные векторы матрицы С,

i-ый столбец матрицы

Eigenvecs(C) - соб-

ственный вектор, отвечающий значению, равному i-му элементу вектора

Eigenvals(С).

Рисунок 7.24. Рабочее окно вычисления собственных значений и собственных векторов матрицы С

Ниже приведены различные способы проверки правильности вычислений собственных значений и собственных векторов:

125

7.8. Решение системы линейных уравнений

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn :

Эта система в «свернутом» виде может быть записана в виде:

n

aij x j bi , где i=1,2,...,n . В соотношении с правилами умножения

i 1

матриц рассмотренная система линейных уравнений может быть записана в матричном виде Ax=b, где

Матрица А называется матрицей системы, матрица-столбец b, называется правой частью системы, а матрица-столбец х – решением системы.

Если матрица системы невырождена (ее определитель отличен от нуля), то у нее существует обратная матрица и тогда решение системы легко получится, умножив обе части уравнения Ax=b слева на матрицу A-1:

A-1(Ax)=A-1b, а поскольку A-1A=E и Ex=x, то x=A-1b.

Задание. Решите систему линейных уравнений: x 2 y 3z 7

x 3y 2z 5 x y z 3

Задайте A - матрицу системы и правую часть - b:

Способы решения системы линейных уравнений:

126

1)Вычислите решение системы через обратную матрицу по формуле x=A-1b и проверьте правильность решения:

2)Решите систему с помощью функции lsolve и сравните результат решения с решением x=A-1b:

Решение системы линейных уравнений методом Гаусса

Метод Гаусса – один из точных методов решения невырожденной системы линейных алгебраических уравнений, его еще называют методом гауссовых исключений. Метод состоит в том, что систему n линейных ал-

гебраических уравнений относительно n неизвестных x1 , x2 ,..., xn :

a11x1 a12 x2 ... a1n xn b1 ,

исключением неизвестных к эквивалентной системе с треугольной матрицей вида:

xn d n

решение которой, находят по рекуррентным формулам:

Задание. Решите ту же систему линейных уравнений методом Гаусса.

Задайте A - матрицу системы и правую часть - b:

Сформируйте расширенную матрицу системы Ar, включающую правую часть системы последним столбцом:

127

1 2 3 7

1 1 1 3

Приведите расширенную матрицу системы Ar к ступенчатому виду при помощи функции rref, выполняя прямой и обратный ходы гауссова исключения:

1 0 0 1

0 0 1 2

Выделите блок матрицы Ag – ее последний столбец, содержащий решение

Решите систему с помощью функции lsolve и сравните с решением, полученным методом Гаусса:

Проверка решения

7.9. Задачи математического анализа

Вычисление пределов функций

Большинство инструментов MathCad для решения задач математического анализа собрано в панели Анализ, которая открывается щелчком по

кнопке в панели математических инструментов. Вид панели представлен на рисунке 7.25.

Кнопки для вычисления пределов, первая вставляет в рабочий документ оператор

128

вычисления предела функции в точке или на бесконечности, вторая и третья кнопки – операторы вычисления односторонних пределов соответственно справа и слева.

Рисунок 7.25. Панель решения задач математического анализа

Задание 1. Вычислить предел функции

Щелкните по свободному рабочему полю, затем по инструменту , в помеченные позиции введите с клавиатуры выражение допредельной функции и предельную точку;

Щелкните по кнопке из меню Символы , результат представлен на рисунке 7.26.

Рисунок 7.26. Результат вычисления предела заданной функции

Задание 2. Вычислите пределы функций:

lime x , lime x

Для первой функции использовать инструмент , а для второй -

, результатом будет следующее:

129

Дифференцирование

Выражение для первой производной функции можно найти при по-

мощи кнопки , рассматриваемого меню, показанного на рисунке 7.25., а для производных более высокого порядка требуется использовать ин-

струмент .

Задание. Вычислите первую производную функции (xx)и вторую производную (xx).

Для вычисления первой производной функции нажмите инструмент

производная - 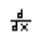, в котором с клавиатуры введите функцию, от которой требуется найти производную - x^x, после этого нажмите пробел столько раз, чтобы выделить дифференциал от функции;

Нажмите на инструмент , после чего щелкните вне выделенного поля, появится рассчитанная производная от функции.

Для вычисления второй производной выбирайте инструмент , в котором n заменить на 2, а в остальном проделать аналогичную предыдущим пунктам работу, в результате будем иметь ниже следующее:

Интегрирование

Символьное вычисление неопределенного интеграла в MathCad мож-

но выполнить при помощи инструмента панели математического анализа .

130