
Основы проектирования электронных средств Материалы к Экз ОПЭС-2014 РК-01-02 / Назаров_Конструирование_РЭС
.pdf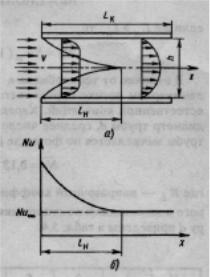
n |
n |
|
, ACP = AK (1− KЗ ); L = åLi Si / åSi |
(5.22) |
|
i=1 |
i=1 |
|
где А к — площадь сечения кожуха конструкции в направлении, перпендикулярном потоку воздуха; KЗ = VЭJJ/VK — коэффициент заполнения; Vэл, VK — объемы элементов и кожуха конструкции соответственно; Li-, Si — длина обтекания и площадь теплоотдающей
поверхности i-ro элемента.
Анализ вынужденного конвективного теплообмена в каналах производится на модели, изображенной на рис. 5.8,а. Канал образован располо-
женными на |
расстоянии h друг от |
|
друга плоскими гладкими |
стенками, |
|
на которых |
равномерно |
распределе- |
ны источники тепла. По каналу протекает воздушный охлаждающий поток, объемный расход которого GV в поперечном сечении на входе в канал постоянен.
Исследования показали [18, |
19], |
||
что |
на начальном |
участке канала |
|
x<lH |
формируется |
профиль |
скоро- |
сти и температуры потока, толщина пограничного слоя постепенно увеличивается от нуля до h/2. На этом участке критерий Нуссельта и, следовательно, коэффициент теплопередачи стенок зависят от длины
канала х (рис. 5.8, б). При х ≥lH пограничные слои потока смыкаются, наступает режим стабилизированного движения воздушного потока,
критерий Нуссельта принимает постоянное значение Nu∞
Изменение критерия Нуссельта по длине канала вызывает необходимость расчета среднего значения Ňu, с помощью которого определяется конвективный коэффициент теплопередачи.
При ламинарном движении воздуха (Re < 2200) длина начального участка канала lH = 0,01hRe, Nu∞ = 4,12.. Среднее значение критерия
Нуссельта для канала малой длины (L к ≤l н) определяют по формуле [19]
183
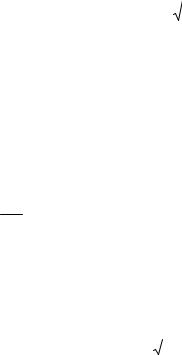
|
|
|
Nu |
= 1.5Nu∞ |
lH / LK |
(5.23) |
Для длинных каналов (L к > l н) |
|
|||||
|
|
= Nu∞ (1+ 0.5lH / LK ) |
(5.24) |
|||
|
Nu |
|||||
При вихревом режиме движения воздуха (l н = 40 h) Nu∞ = 0,19Re0.8. Среднее значение критерия Нуссельта в случае L к ≤ l H находят как
Nu |
= 1,165Nu∞ (lH / LK ) |
(5.25) |
если же L к > lH то
Nu = Nu∞ (1+0.5lH / LK )
В отличие от теплообмена в каналах теплообмен внутри трубы при ламинарном потоке определяется факторами как вынужденной, так и естественной конвекции. Характерным размером служит внутренний диаметр трубы d, среднее число Нуссельта для воздуха по всей длине трубы вычисляется по формуле [19]
|
Nu |
= 0.133 |
|
Re |
Gr0.1 × KL , |
(5.27) |
где KL — поправочный коэффициент |
на длину трубы, |
значения кото- |
||||
рого в зависимости от отношения длины трубы l к внутреннему диаметру d приведены в табл. 5.4.
Таблица 5.4
l/d |
1 |
2 |
5 |
10 |
15 |
20 |
30 |
50 |
KL |
1,9 |
1,7 |
1,44 |
1,28 |
1,17 |
1,08 |
1,05 |
1,0 |
|
|
|
|
|
|
|
|
|
При вихревом режиме движения теплоносителя коэффициент теплопередачи и эффективность теплообмена мало зависят от граничных условий на поверхности стенок канала или трубы. В то же время на теплообмен существенно влияют начальная турболизация потока и форма входной кромки канала. Эти условия определяют длину начального участка тепловой стабилизации l н. В случае вынужденной конвекции в
трубе диаметром d длина начального участка lH = ( 15...30)d Значение
критерия Нуссельта на стабилизированном участке в неограниченной прямой трубе
Nu |
∞ |
= 0.023Re |
0.8 Pr0.43 (Pr |
f |
/ Pr )0.25 (5.28) |
|
|
|
w |
184
В результате преобразования (5.28) получено [18, 19] справедливое для воды и воздуха соотношение для расчета среднего значения конвективного коэффициента теплопередачи в изогнутой и ограниченной трубе:
a∞ = Zv0.8K'L(1 +1 .8d/R)/d0.2, |
(5.29) |
где Z — параметр, учитывающий физические свойства теплоносителя;
К'L — коэффициент, учитывающий ограничение длины трубы; R — радиус изгиба трубы. Значения параметра Z для воды и воздуха приведены в табл. 5.5, значения поправочного коэффициента — в
табл. 5.6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tf.c |
|
|
-50 |
|
-20 |
|
|
|
0 |
|
20 |
50 |
100 |
|||||
Z (воздух) |
|
4,3 |
|
3,92 |
|
|
3,74 |
|
3,56 |
3,4 |
3,1 |
|||||||
Z (вода) |
|
|
— |
|
— |
|
|
1430 |
|
1,880 |
2500 |
3190 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Re |
|
|
|
|
|
К ‘L при разных отношениях I /d |
|
|
||||||||||
|
1 |
|
|
2 |
|
5 |
|
10 |
|
15 |
|
30 |
|
50 |
||||
1∙104 |
1,65 |
|
|
1,5 |
|
1,34 |
|
1,23 |
|
1,17 |
|
1,07 |
|
1,0 |
||||
2∙ 04 |
1,51 |
|
|
1,4 |
|
1,27 |
|
1,18 |
|
1,13 |
|
1,05 |
|
1,00 |
||||
6∙104 |
1,34 |
|
|
1,27 |
|
1,18 |
|
1,13 |
|
1,10 |
|
1,04 |
|
1,00 |
||||
1∙ 05 |
1,28 |
|
|
1,22 |
|
1,15 |
|
1,10 |
|
1,08 |
|
1,03 |
|
1,00 |
||||
1∙106 |
1,14 |
|
|
1,11 |
|
1,08 |
|
1,05 |
|
1,04 |
|
1,02 |
|
1,00 |
||||
На участке нестабилизированного движения теплоносителя в трубе х ≤ lH = 20 d при вихревом режиме значение числа Нуссельта
на расстоянии х определяется выражением |
|
||
Nu = (lH/x)1/6(Nu∞,) |
(5.30) |
||
среднее значение критерия на участке длиной х — выражением |
|
||
|
|
= 1.2(lH/x)1/6(Nu∞,)). |
(5.31) |
|
Nu |
||
Теплофизические параметры теплоносителя, через которые вычисляются критерии, входящие в формулы (5.17) — (5.21), (5.27), (5.28), бе-
185
рут из таблиц для средней температуры теплоносителя tj = 0,5 (t8Х +t вых), где t вх,tвых—температуры теплоносителя на входе и выходе канала или трубы.
5.1.4. Передача тепла излучением
Процесс теплообмена излучением основан на способности твердых, жидких и газообразных тел излучать и поглощать тепловую энергию в виде электромагнитных волн инфракрасного диапазона.
Для двух тел, участвующих во взаимном теплообмене излучением (или для тела, помещенного в газовую среду), результирующий тепловой поток, направленный от изотермической поверхности S 1 первого
тела с температурой t1 ко второму телу (или газовой среде) с температурой t2 определяется соотношением, полученным на основании закона Стефана— Больцмана [18]:
|
|
|
|
|
|
|
|
é |
|
+ 273 |
ö |
4 |
æ t2 |
+ 273 |
ö |
4 |
ù |
|
P = С |
ε |
|
ϕ |
|
S |
|
æ t1 |
|
|
|
||||||||
|
|
|
êç |
|
|
÷ |
|
- ç |
|
|
÷ |
|
ú |
|||||
|
|
|
|
100 |
|
|
100 |
|
||||||||||
Л |
0 |
|
ПР |
|
12 |
|
1 |
è |
|
ø |
|
è |
|
ø |
|
ú |
||
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
û |
где С 0 = 5,670 Вт/(м2 • К4 ' — коэффициент излучения абсолютно черного тела; ε — приведенная степень черноты поверхностей тел, участвующих в теплообмене; φ 12— коэффициент взаимной облученности тел.
При теплообмене неограниченных плоскопараллельных пластин, поверхности которых характеризуются степенями черноты ε1 и ε2 ,
приведенная степень черноты
ε ПР |
= |
|
|
1 |
|
|
|
(5.33) |
||
1./ε1 |
+1/ε 2 -1 |
|||||||||
|
|
|
||||||||
Для теплообмена в замкнутом пространстве |
|
|
|
|
||||||
ε ПР = |
|
|
|
|
1 |
|
|
|
(5 34) |
|
1./ε1 + (1/ ε2 |
-1)S1 / S2 |
|||||||||
|
' |
|||||||||
где S 1, S 2 — площади поверхностей первого и второго тел. |
|
|||||||||
Значения степени черноты |
некоторых |
материалов |
приведены в |
|||||||
табл. П.4. |
|
|
|
|
|
|
|
|
|
|
Коэффициент φ 12 показывает, какая часть теплового потока, испускаемая нагретым телом, поглощается холодным. Как правило, в расчетах тепловых режимов РЭС полагают φ 12 =1.
186

Для практических расчетов выражение (5.32) преобразуется к виду
Pл = αлS1(t1-t22)- |
(5-35) |
Здесь ал =εПРφ12f(t1,t2) — коэффициент теплопередачи излучением, где
|
æ t1+ 273 |
ö |
æ t2 + 273 |
ö |
|||
|
ç |
|
÷ |
- ç |
|
|
÷ |
|
100 |
|
100 |
||||
f (t1,t2) = 5.673 |
è |
ø |
è |
|
ø (5.36) |
||
|
|
t1 |
- t2 |
|
|
||
5.1.5. Определение конвективного и лучевого коэффициентов теплопередачи по номограммам
Моделирование процесса теплообмена между конструкциями РЭС и средой для меняющихся в широких пределах исходных данных позволило найти аппроксимирующие выражения конвективных и лучевых коэффициентов теплопередачи в виде функций конструктивных параметров, по которым построены номограммы для нахождения этих коэффициентов.
Многообразие номограмм определяется различием в подходах к решению задачи расчета теплообмена.
Структура номограммы и схема определения конвективного коэффициента теплопередачи а к в условиях естественной конвекции в неограниченном пространстве изображена на рис. 5.9.
Для определения а к необходимо задать начальный перегрев поверхности теплообмена t = t1-t2 , где t1 — температура на поверхности теплообмена; t2 — температура окружающей среды, вычислить среднее значение температуры окружающей среды tCP = 0,5 (t1+t2) и опре-
деляющий размер нагретого тела (конструкции) L = 
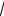 S / 6 , где S — пло-
S / 6 , где S — пло-
щадь поверхности теплообмена. Затем соединить прямой точки tCP и |
t, из |
|
точки пересечения этой прямой со вспомогательной |
линией |
А |
провести прямую в точку L. На пересечении данной линии |
со шкалой |
|
а к считывается значение конвективного коэффициента теплопередачи. Номограмма для определения коэффициента теплопередачи излу-
чением аK приведена на рис. 5.10. Номограмма построена для степени черноты поверхности εн = 0,8. Значение коэффициента теплопередачи считывают в точке пересечения шкалы а K с прямой, соединяющей точ-
187
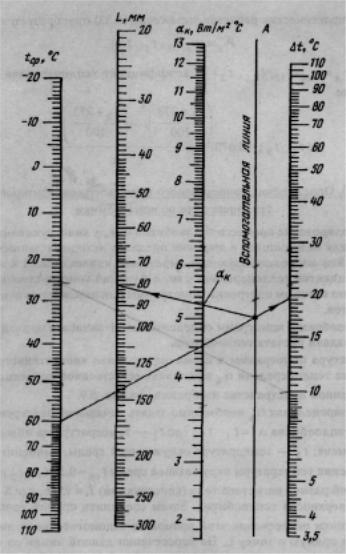
Рис. 5.9. Номограмма для определения конвективного коэффициента теплопередачи
ки t2 и t2 на температурной шкале. Пересчет коэффициента теплопередачи, найденного с помощью номограммы, на реальную степень черноты поверхности теплообмена е производится по формуле
188
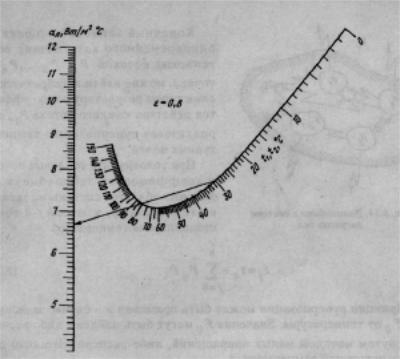
Рис. 5.10. Номограмма для определения коэффициента теплопередачи излучением
'
а л = а л н ε / ε H
где а л н — значение коэффициента теплопередачи, определенного по номограмме.
5.1.6. Принципы суперпозиции температурных полей и местного влияния
Конструкция РЭС представляет собой систему нагретых тел, рассеивающих тепловые потоки Р i и находящихся во взаимном теплообмене
друг с другом, с некоторой j-й точкой и окружающей средой (рис. 5.11). Если рассмотреть воздействие каждого теплового потока на точку у обособленно от воздействия других потоков, то становится очевидным, что температура tj этой точки, каждый раз оказывающейся на
некоторой изотермической поверхности, обусловлена тепловым коэффициентом F ij между источником тепла с тепловым потоком Рi . и
изотермической поверхностью.
189

Рис. 5.11. Теплообмен в
системе нагретыхтел
Конечный тепловой |
эффект |
от |
одновременного воздействия |
всех |
|
тепловых потоков Р 1 г Р 2 |
Рп |
в |
Точке j можно найти алгебраическим сложением результирующих эффектов действия каждого потока Рi, т.е.
реализовав суперпозицию температурных полей.
При условии, что тепловые потоки и коэффициенты теплообмена отдельных областей системы на зависят от температуры, в любой j'-й точке стационарная температура
n |
|
t j = tC + åFijPi |
(5.37) |
i=0
Принцип суперпозиции может быть применен и в случае зависимости Fij от температуры. Значения Fij могут быть найдены либо расчетным путем методом малых приращений, либо экспериментально для результирующей температуры t j.
Рис. 5.12. К пояснению принципа местноговлияния
При анализе температурных полей наретых тел часто требуется определить, а каком расстоянии от области, занятой сточником тепла, конфигурация этой бласти практически не влияет на конэигурацию температурного поля в теле. 1 ряде работ показано [18], что если исочник занимает область J(рис. 5.12) и авномерно распределен в этой области, о на расстоянии L от центра области по величине примерно равном наиболь1ему размеру области) характер темпеатурного поля такой же, как и в случае, ели тепловой поток сосредоточен в ентре области.
Иными словами, любое местное возущение температурного поля локально не распространяется на отдельные частки этого поля.
В качестве примера можно привести температурное поле группы радиоэлементов, расположенных на плате узла РЭС и являющихся источниками тепла. Эта группа элементов вызывает такое же повышение температуры в отдельных частях аппарата, как и равномерно распределенный на плате источник той же мощности. Вблизи от радиоэлементов температурное поле в значительной степени зависит от размеров и конфигурации самих элементов.
5.1.7. Электротепловая аналогия
Формулы (5.2), (5.3) и (5.35), устанавливающие зависимость между тепловыми потоками и перегревом, аналогичны формуле закона Ома в
интегральной форме для электрических цепей: |
|
I = σ(φ1-φ2). |
(5.38) |
Это позволило использовать методы и приемы теории |
электриче- |
ских цепей для интерпретации процессов теплообмена. |
|
Из сравнения соотношений для тепловых потоков и электрического тока, протекающего через участок электрической цепи, легко установить следующие аналогии:
электрическое сопротивление R э — тепловое сопротивление R; электрическая проводимость σэ — тепловая проводимость σ;
электрическое напряжение U — температурный перегрев t; электрический потенциал φ — температура t; электрический ток I— тепловой поток Р.
На основании электротепловой аналогии процесс теплообмена может быть представлен тепловой схемой, элементами которой являются источники и приемники тепловой энергии и тепловые сопротивления (проводимости). Каждому узлу тепловой схемы ставится в соответствие определенная температура t. Переменные величины в тепловой схеме (тепловые потоки и перегревы) подчиняются законам Ома и Кирхгофа для тепловых схем. На основании этих законов тепловые схемы могут быть преобразованы и упрощены.
Как следует из (5.2), (5.3), (5.35) и (5.38), тепловые проводимости (сопротивления) тепловой схемы определяются с помощью соотношений:
при кондуктивной теплопередачи
σ |
Т |
= λSCP |
= α |
T |
S |
CP |
; R = |
1 |
|||
|
|||||||||||
|
l |
|
|
|
T |
αT SCP |
|||||
|
|
|
|
|
|
|
|
|
|
||
при передаче тепла конвекции |
|
|
|
|
|
|
|
|
|
||
|
|
σк=αкS; |
Rk = |
|
1 |
|
|
||||
|
|
αk S |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
191
при передаче тепла излучением |
|
|
σЛ=αЛS; Rл = |
1 |
|
α л S |
||
|
Таким образом, тепловые проводимости (сопротивления) выражаются через теплофизические параметры материалов (среды) и геометрические (конструктивные) характеристики нагретых тел.
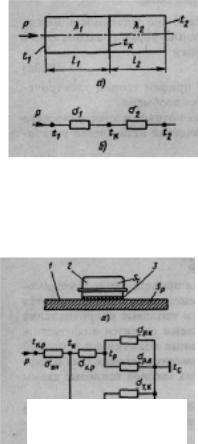
Пример 5.1. Через цилиндрический стержень диаметром d, составленный из двух разнородных материалов с коэффициентами теплопроводности λ1, и λ2 (рис. 5.13, а), протекает тепловой поток Р. Составить тепловую схему процесса теплопередачи и
при известной температуре t2 правого
|
конца найти температуру t K в контакте |
|||
|
материалов и температуру t 1. |
|||
|
Тепловая схема представлена на рис. |
|||
|
5.13,Поскольку |
|
|
|
|
P = σ2(tK-t2) = σ1(tl-tK), |
|
||
|
то |
|
|
|
Рис. 5.13. Передача |
tK = t2 + P/σ2; |
t1=tk + P/σ1 |
|
|
тепла в ци- |
Для кондуктивной теплопередачи |
|||
линдрическом стержне: |
||||
а — конструкция |
σ1 = λ1πd |
2 |
λ2πd |
2 |
|
σ 2 = |
|
||
|
4l1 |
|
4l2 |
|
Рис. 5.14.
Теплообмен транзистора, установленного
на радиаторе:
а — схематическое изображение конструкции; б — тепловая схема; 1 — радиатор; 2 — транзистор; 3 — прокладка
Пример |
5.2. |
Составить |
тепловую |
схему, отражающую |
процесс |
теплопере- |
|
дачи от транзистора, установленного на радиаторе с площадью теплоотводящей поверхности Sp (рис. 5.14, а), к среде, если на кристалле транзистора выделяется мощность Р.Тепловая схема приведена на рис5.14,.
б. Тепловой поток от кристалла транзистора через внутреннюю проводимость σ вн передается на корпус транзистора, через проводимость σKP контакта
«корпус транзистора — радиатор» — на радиатор и с радиатора конвективным и лучевым способами — среде. Одновре-
менно часть теплового потока конвек-
