Основы проектирования электронных средств Материалы к Экз ОПЭС-2014 РК-01-02 / Назаров_Конструирование_РЭС

тате приближенного решения уравнения (4.16) по методу Рэлея или по методу Ритца.

Согласно методу Рэлея частота свободных колебаний ω0 определяется в результате сопоставления выражений для кинетической и потенциальной энергий колебаний системы. Метод позволяет учесть нагружение платы функционального узла установленными на ней элементами и получить соотношение для расчета частоты свободных колебаний пластины, справедливое при любых краевых условиях. Формула Рэлея, позволяющая найти частоту свободных колебаний основного тона нагруженной пластины, имеет вид

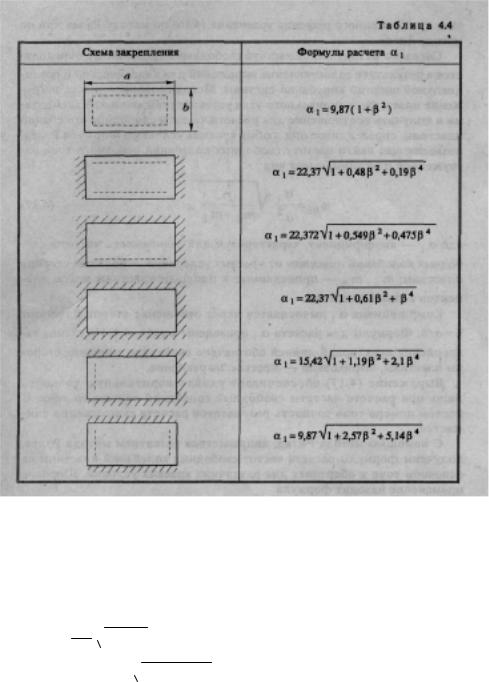
где α1 — коэффициент, характеризующий зависимость частоты свободных колебаний пластины от краевых условий; α — большая сторона пластины; тэ,т0 — приведенные к площади пластины массы элементов и самой пластины.

Коэффициент α1 вычисляется через отношение сторон пластины

β=a/b. Формулы для расчета α1 приведены в табл. 4.4. На схемах закрепления пунктирной линией обозначено свободное опирание сторо-

ны пластины, штриховкой — жесткое закрепление.

Выражение (4.17) обеспечивает удовлетворительную точность лишь при расчете частоты свободных колебаний основного тона. С ростом номера тона точность результатов расчета существенно снижается.

С помощью метода Ритца, являющегося развитием метода Рэлея, получены формулы расчета частот свободных колебаний пластины на основном тоне и обертонах для различных краевых условий. Широкое применение находит формула

где αi — коэффициент, зависящий от способа закрепления пластины,

соотношения ее сторон и номера тона колебаний; т — масса пластины, приведенная к площади; КЭ — коэффициент, учитывающий нагрузку

пластины размещенными на ней элементами.

Значение αi. находят в результате решения дифференциального уравнения колебаний прямоугольной пластины при заданных краевых

143

условиях. Для определенных комбинаций краевых условий и отношений сторон пластины αi - табулирован.

Для упрощения процедуры расчета круговой частоты свободных колебаний пластины основного тона формула (4.18) преобразуется:

где C = 2απ1 D / m0 - частотная постоянная; а — большая сторона пла-

стины, мм; KM = EρC / EC ρ - поправочный коэффициент на матери-

144

ал пластины; Е, Е с — модули упругости материала пластины и стали; ρ,ρс — их плотности; KЭ = 1/ 1+ mЭ / mП -поправочный коэффициент на

нагружение пластины равномерно размещенными на ней элементами; т э

— масса элемента; т п — масса пластины.

Значения частотной постоянной С для некоторых схем закрепления пластины приведены в табл. 4.5.

Построение расчетных моделей функциональных узлов производится на основе анализа реальных конструкций и выявления характерных особенностей, оказывающих существенное влияние на динамические процессы при вибрации. Ниже приводятся примеры моделирования некоторых конструкций функциональных узлов. Узел, выполненный на печатной плате, закрепляемой в четырех точках по углам (рис. 4.19,а), представляют расчетной моделью пластины, равномерно нагруженной радиоэлементами, со свободным опиранием всех сторон (рис. 4.19,6). Принятый способ закрепления обосновывается тем, что при изгибных колебаниях основного тона на каждой стороне пластины укладывается полуволна, узлы перемещения совпадают с точками крепления платы. Поэтому наличие точек закрепления не сказывается на параметрах колебаний.

Расчетной моделью узла на печатной плате с размерами сторон а и Ь, закрепленной в шести точках по контуру (рис. 4.20, а), служит прямоугольная пластина с размерами сторон а/2, Ь, свободно опирающаяся по контуру, с равномерно распределенной нагрузкой (рис. 4,20, б). Основной тон свободных колебаний определяется полуволной, укладывающейся вдоль сторон α/2 и b пластины.

Конструкция функциональной ячейки блока разъемного типа (рис. 4.21, а) может быть представлена расчетной моделью в виде нагруженной прямоугольной пластины с жестким закреплением двух сторон, на которых установлены контрольная колодка 3 и электрический соединитель 2, и свободным опиранием двух других сторон (рис. 4.21, б). Принятая схема закрепления обосновывается тем, что электрический соединитель и контрольная колодка по сравнению с печатной платой имеют значительно большую жесткость на изгиб, а расстояние между стенками направляющих, с помощью которых плата устанавливается в блоке, в большинстве случаев существенно превышает толщину печатной платы.

Каркасные конструкции функциональных ячеек (печатная плата закреплена на рамке по контуру) обычно моделируют пластиной с жестким закреплением всех сторон. Другой подход к построению расчетных моделей таких конструкций изложен в следующем разделе.

145

Таблица 4.5

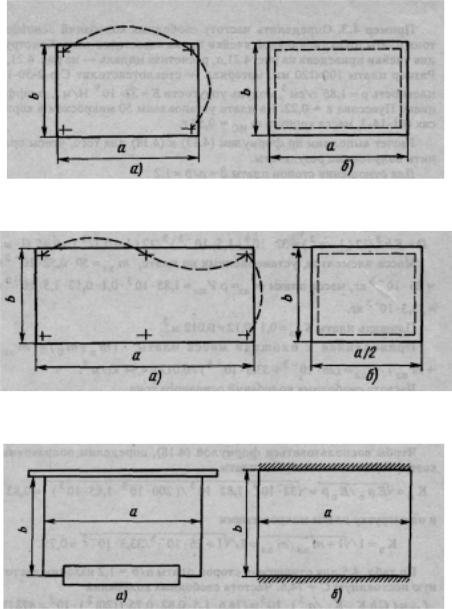
Рис. 4.19. Построение расчетной модели платы, закрепленной в четырех точках поуглам:

а — конструкция платы; б — расчетная модель

Рис. 4.20. Построение расчетной модели платы, закрепленной в шести точках поконтуру:

а — конструкция платы; б — расчетная модель

Рис. 4.21. Построение расчетной модели функциональной ячейки блока разъемноготипа:

а — конструкция платы; б — расчетная модель

147

Пример 4.3. Определить частоту свободных колебаний основного тона платы функциональной ячейки блока кассетного типа. Конструкция ячейки приведена на рис. 4.21,а, расчетная модель — на рис. 4.21, б. Размер платы 100x120 мм, материал — стеклотекстолит Сф-2-50-1,5, плотность ρ = 1,85 г/см3 , модуль упругости Е= 32•109Н/м2 , коэффициент Пуассона ε = 0,22. На плате установлены 50 микросхем в корпусах 401-14-3, масса корпуса т ис = 0,52 г.

Расчет выполним по формулам (4.17) и (4.18) для того, чтобы сравнить полученные результаты.

Для отношения сторон платы β = а/b = 1,2

α1 = 22.371+ 0.48β 2 + 0.19β 4 = 22.37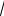1+ 0.691+ 0.393 = 32.3a,

Цилиндрическая жесткость платы

D=Eh3/12(1-ε2) = 32·109(1,5·10-3)3/12( 1-0,222) = 9,45 Н-м .

Масса элементов, установленных на плате, т эл = 50 • 0,5210 ~ =

=26·10-3кг, масса платы mпл=рVпл= 1,85·103·0,1·0,12· 1,5·10-3 =

=33,3·10-3 кг.

Площадь платы SПЛ = 0,1·0,12=0,012 м2.

Приведенная к площади масса платы (т э + т0) = (т эл + mпл)/Sпл=(26· 10-3 +33,3·10-3)/0,012=4,94 кг/м2.

Частота свободных колебаний основного тона

Чтобы воспользоваться формулой (4.18), определим поправочные коэффициенты на материал платы

KM = EρC / EC ρ = 32 ×109 ×7.82 ×103 /(200 ×109 ×1.85×103 = 0.82

и на нагрузку платы микросхемами

KЭ = 1/ 1+ mЭЛ / mпл = 1/ 1+ 26 ×10−3 / 33.3×10−3 = 0.75

По табл. 4.5 для отношения сторон платы а/b = 1,2 находим частотную постоянную С = 74,6. Частота свободных колебаний

f01 = (СhКмКэ/а2)·105 = (74,6·1,5·0,82·0,75/(120)2)·105 = 478Гц.

Таким образом, расхождение результатов расчета частоты свободных колебаний основного тона пластины по формулам (4.17) и (4.18) лежит в пределах 3,5%.

148

4.3.4. Расчет частоты свободных колебаний функциональных узлов сложных конструкций

Понятие «сложные конструкции» охватывает функциональные узлы, усиленные ребрами жесткости, рамками, обечайками и другими элементами, повышающими жесткость конструкции.

Частота свободных колебаний основного тона таких конструкций может быть найдена по формуле Рэлея (4.17). Применение формулы (4.17) предполагает переход от сложной конструкции узла к модели эквивалентной прямоугольной пластины с параметрами a, D и m0=(mэл+тпл)/Sпл. Жесткость эквивалентной пластины на изгиб находят как D = D пл + Dp , где D пл, Dp — цилиндрическая жесткость

платы и рамки на изгиб соответственно.

Расчет цилиндрической жесткости платы производят по формуле

где Е — модуль упругости материала платы; J— момент инерции сечения платы в плоскости изгиба; b — ширина сечения; ε — коэффициент Пуассона для материала платы.

Значение D можно найти также с помощью (4.20), если подставить

в формулу момент инерции сечения рамки.

Ввиду того что сечение рамки или других элементов, повышающих жесткость конструкции узла, имеет сложную конфигурацию, момент инерции сечения определяют как сумму осевых и центробежных моментов элементарных сечений правильной геометрической формы, на которые разбивается исходное сечение:

где Ji,., l2i,- Fi — осевой и центробежный моменты i'-го элементарного сечения соответственно; Fi — площадь этого сечения; li,- — расстояние

в плоскости изгиба сечения между центрами тяжести ЦТ i-го элементарного сечения и сечения рамки.

Подход к определению момента инерции сечения рамки иллюстрируется с помощью рис. 4.22.

Соотношения для расчета осевых моментов инерции сечений простейших геометрических форм и координат центра тяжести приведены в приложении (табл. П.1).

149

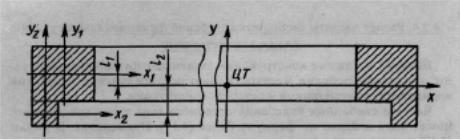
Рис. 4.22. К расчету момента инерции сечения рамки

При выборе сечения рамки необходимо исходить из принципа наихудшего случая: жесткость конструкции на изгиб в сечении должна быть минимальной, что позволит найти самую низкую частоту свободных колебаний конструкции узла.

Коэффициент а,-, входящий в формулу (4.18), при конкретном закреплении сторон определяют по таблицам, приведенным в [64]. В случае закрепления пластины в четырех или шести точках по периметру, значение a j может быть найдено по формуле:

α1=π2(1+a2/b2),

где а , b — длина и ширина пластины.

4.4. Расчет ударопрочности конструкций РЭС

Конструкция РЭС отвечает требованиям ударопрочности, если перемещение и ускорение при ударе не превышают допустимых значений, а элементы конструкции обладают запасом прочности на изгиб. В связи с тем что изгибные напряжения в элементах конструкции в конечном счете определяются величиной перемещений (прогибов), расчет ударопрочности конструкций может быть сведен к нахождению запаса прочности элементов при прогибе.

Исходными данными для расчета являются: масса т и геометрические размеры элемента конструкции; характеристики материала (модуль упругости Е, Па; плотность ρ , кг/м3 ; коэффициент Пуассона ε); перегрузки при ударе пУД и длительность удара i, с). Основу методики

расчета составляют соотношения, приведенные в разд. 4.22.

Прежде всего, по заданным параметрам удара необходимо определить амплитуду ускорения при ударе а тах = пУД g, значение скорости в

150

начальный момент удара vо = αmaxτ или эквивалентную высоту падения массы Н0 = V20/2g .

Далее находят частоту свободных колебаний конструкции f0 , по

значению которой вычисляется максимальный прогиб упругого элемента при ударе. В зависимости от модели, к которой приводится реальная конструкция, расчет частоты свободных колебаний производит-

ся по формулам (4.15), (4.17)—(4.19).

Составляющим максимального прогиба упругого элемента конструкции при ударе является статический прогиб zCT=mg/k . Неизвестное значение жесткости конструкции k в выражении для zCT можно найти, если соотношения (4.15), (4.17)—(4.19) преобразовать к виду

f01 = 21π 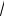k / m . Так, например, воспользовавшись формулой (4.15) для

основного тона колебаний, получим k = EJλ21. /l3 . Из формулы Рэлея

(4.17) найдем k = Da31b/a3 т.д. Другой подход к определению жесткости конструкции состоит в использовании значения частоты свободных колебаний. Из основной формулы для расчета частоты свободных

колебаний следует, что k = (2 πf01)2 т .

Знание статического прогиба zст, скорости VQ в начальный момент удара и частоты свободных колебаний f01 позволяет найти максимальный прогиб упругого элемента (максимальное перемещение массы)

Zmax= 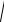zCT2 + (v0 / 2πf01 )2

и полную динамическую деформацию упругого элемента z Д = zCT + zmax = zCT (1+ 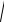1+ (v0 / 2πf01 zCT ).

Полная динамическая деформация определяет эквивалентную силу удара, приложенную к упругому элементу в точке удара: РУД =kzД.

Допустимое напряжение в элементах конструкции при изгибе σ = σ/n , где σ — предельное напряжение в материале; п = п j п 2 п 3

— коэффициент, характеризующий запас прочности: n1= 1,25... 1,5 — коэффициент достоверности определения расчетных нагрузок и напряжений; п2 = 1,0...1,5 — коэффициент, характеризующий степень ответственности детали; п3 = 1,2...3 — коэффициент, учитывающий однородность механических свойств материалов.

151

Изгибное напряжение, возникающее в элементах конструкции при ударе, можно найти через изгибающий момент М и и момент сопротивления изгибу Wи по формуле σи = М и /Wи . При расчете изгибающего момента исходят из того, что сила РУД приложена в геометрическом

центре упругого элемента. Тогда реакция опор упругого элемента составит Р = РУД/ 2 , а изгибающий момент М и = РР α/2, где a — геометрический размер элемента конструкции в плоскости изгиба.

Момент сопротивления упругого элемента изгибу WK=J/ymax, где

J— момент инерции сечения элемента относительно оси изгиба; ушах = h/2 — значение координаты от нейтральной оси сечения до поверхности упругого элемента; h — толщина упругого элемента.

Пример 4.4. Прямоугольное основание из сплава Д16Т, покрытое диэлектрическим слоем А12 О 3 (поликор) и закрепленное в четырех точках по углам, подвергается удару длительностью τ = 5·10-3 с при максимальной перегрузке пУД = 150 единиц. Проверить условия ударопрочности конструкции, если размеры основания LX=LY = 0,2м, толщина пластины h1 = l,5-10~3M, толщина диэлектрического покрытия

h2 = 0,25·10-3м.

При решении задачи примем следующие допущения: жесткость конструкции определяется жесткостью металлического основания; расчетной моделью конструкции является прямоугольная пластина со свободным опиранием всех сторон (см. рис. 4.19, б), нагруженная равномерно распределенной массой диэлектрического слоя; прогиб диэлектрического слоя при ударе равен прогибу основания. Решение задачи состоит в определении напряжений, возникающих в основании и диэлектрическом слое при прогибе под действием удара.

Амплитуда ускорения при ударе

αmах = nудg=150·9.8=1470м/с2

Начальная скорость в момент удара

v0 = ашахτ=1470·5·10-3 = 7,35 м/с.

Для расчета частоты свободных колебаний пластины воспользуемся формулой (4.19). При свободном опирании пластины по контуру и от- ' ношении сторон а/b = 1 частотная постоянная С = 45,8. Масса пластины т п =

2,76 10 3 • 0,2 • 0,2 • 1,5 • 10-3 = 0,166 кг; масса диэлектрического

152