
Основы проектирования электронных средств Материалы к Экз ОПЭС-2014 РК-01-02 / Назаров_Конструирование_РЭС
.pdf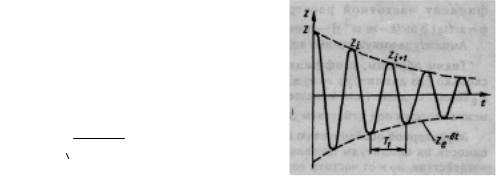
Поскольку параметры свободных колебаний определяются только состоянием самой системы, правую часть уравнения (4.4) полагают равной нулю. Уравнение становится однородным.
Решение уравнения при начальных условиях |
Ż(0)=z(0)=0,z(0)=V |
и отсутствии демпфирования (δ = 0) имеет вид |
|
z = (v/ω0) sin ωо t = Z sin ω0t, |
(4.5) |
где Z = v/ω 0 — амплитуда свободных колебаний.
Из уравнения (4.5) следует, что свободные колебания протекают на частоте со 0, амплитуда колебаний зависит от начальных условий (мгновенной скорости к, сообщенной массе в начальный момент времени). Частота свободных колебаний определяется жесткостью упругого элемента k и массой т конструкции.
Если учесть, что реальным системам присуще затухание δ≠0, то решение однородного дифференциального уравнения свободных колебаний дает следующее соотношение для перемещения:
z = (v/ω0) e-δtsinω1t, (4.6)
где ω1 = 
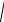 ω02 −δ 2 -частота колебаний. Так как ω0 >> 5, то принимают ω1 ≈ ω 0.
ω02 −δ 2 -частота колебаний. Так как ω0 >> 5, то принимают ω1 ≈ ω 0.
Выражение (4.6) представляет собой затухающее колебание с пери-
одом Т1 = 2 π≠ω1 (рис. 4.4). Затухание свободных колебаний количественно можно характеризовать логарифмическим декрементом колебаний
λ = ln(Zi/Zi+l) = ln(e-δt / e-δ(t+T1 )) =δ T1,
где Zi, Zi+l — значения предыдущей и последующей амплитуд колебаний
соответственно.
Таким образом, свободные колебания в системах существуют непосредственно после внешнего воздействия на отрезке времени, в конце
которого множитель е-δt и, следовательно, амплитуда перемещения становятся равными нулю.
123

Вынужденные колебания в системе протекают под действием внешней гармонической силы Р = Р 0 sin ω t.
Общее решение уравнения (4.3) может быть представлено в виде суммы решения (4.5) однородного уравнения и частного решения, соответствующего гармонической силе Р :
z = Z e-δt sin(ω0t-φ0) + μZCTsin(ωt-φ). |
(4.7) |
||
Перемещение при вынужденных колебаниях |
|
||
|
|
zB = μzCTsin(ωt-φ). |
(4.8) |
Здесь μ = 1/ |
|
—коэффициент динамичности системы, |
|
4δ0v2 + (1− v2 )2 |
|||
где 0= /ω0 |
— коэффициент затухания ; v=ω/ω0 — |
коэффициент |
|
частотной расстройки или частотное отношение;
φ = arctg [ β ω/(k - т ω2 )] — начальная фаза вынужденных колебаний. Амплитуда вынужденных колебаний Z в = μ z ст, откуда μ = ZB/Z ст.
Таким образом, коэффициент динамичности ц показывает, во сколько раз амплитуда вынужденных колебаний при действии силы РQsinωt больше (или меньше) статического прогиба упругого элемента системы под действием силы P0.
Характерной особенностью вынужденных колебаний является зависимость их амплитуды не только от параметров системы и внешнего воздействия, но и от частоты возмущающей силы со. Максимальное значение коэффициента динамичности
μmax =1/(2δ0 
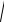 1− δ02 )
1− δ02 )
соответствует коэффициенту частотной расстройки v = (
 1− δ02 )
1− δ02 )
Зависимость коэффициента динамичности от частотной расстройки v приведена на рис. 4.5. Если частота возмущающей силы со совпадает с частотой свободных колебаний (v = 1), то возникает явление механического резонанса, при котором амплитуда вынужденных колебаний достигает максимальной величины, а при отсутствии затухания становится бесконечно большой. Поэтому исключение механических резонансов выбором частот свободных колебаний механических систем за пределами диапазона частот внешних вибрационных воздействий — одно из необходимых условий обеспечения вибропрочности.
Модель механической системы с кинематическим возбуждением приведена на рис. 4.6.
124

Рис. 4.5. Зависимость коэффициента дина- |
Рис. 4.6. Модель механической |
мичности отчастотнойрасстройки |
системыскинематическим |
|
возбуждением |
Внешнее вибрационное воздействие P=РQsinωt приложено к основанию (платформе), которое перемещается по гармоническому закону zа=Zasinωt, где Z а - амплитуда виброперемещения основания.
Движение системы подчиняется уравнению
mž + β(ż-ża) + k(z-za) = 0, |
(4.9) |
где разность перемещения массы и основания (z-za) характеризует
упругую деформацию системы.
После подстановки в (4.9) частного решения для вынужденных колебаний (4.8) и выражения для перемещения основания уравнение движения системы приводится к виду
(-mω2+jωβ + k)z = (jωβ +k)za
откуда находят передаточную функцию
F(j ω) = z/z a = (k+ jωβ) /(k-m ω2+ jωβ )
и амплитуду колебаний системы
1+ 4δ 2v2
ZB = ZA  0
0
(1− v2 )2 + 4δ02v2
Отношение амплитуд перемещения массы и основания
125

|
η = ZB / ZA |
= |
|
|
|
1+ 4δ02v2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
− v2 )2 + 4δ02v2 |
|
||||||||||
|
|
|
(1 |
|
|||||||||
|
носит название коэффициента пере- |
||||||||||||
|
дачи вибраций. Зависимость ц от ко- |
||||||||||||
|
эффициента |
|
частотной |
|
|
расстройки |
|||||||
|
v приведена на рис. 4.7. Как видно из |
||||||||||||
|
рисунка, коэффициент передачи г| |
||||||||||||
|
становится меньше единицы, если |
||||||||||||
|
значение |
v |
превышает |
|
2 |
. Эта осо- |
|||||||
|
бенность |
в |
поведении |
коэффициента |
|||||||||
Рис. 4.7. Зависимость |
передачи |
|
вибраций |
|
используется |
||||||||
коэффициента передачивибраций |
для организации |
|
виброзащиты |
кон- |
|||||||||
отчастотнойрасстройки |
струкций |
|
(виброизоляции) с |
по- |
|||||||||
|
|
||||||||||||
мощью амортизаторов.
4.2.2. Воздействие удара на систему с одной степенью свободы
Анализ ударных воздействий имеет целью определение деформаций и механических напряжений, возникающих в элементах конструкции в зависимости от величины и характера ударных нагрузок. Как отмечалось в разд. 4.1, для упрощения анализа ударные импульсы различной формы приводят к эквивалентному прямоугольному импульсу, используя зависимость
t +τ
a0τ0 = òa(t)dt
t
где a0, τO — ускорение и длительность прямоугольного эквивалентного ударного импульса соответственно; а, τ — ускорение и длительность ударного импульса произвольной формы соответственно. Расчеты показывают [25], что для синусоидального импульса (см. рис. 4.1, б) можно принять a0= 0,63а , τ 0 = τ , для косинусоидального импульса —
а0 = 0,5а, τ0= 1,27τ. Аналогичные соотношения нетрудно получить
для трапецеидального и треугольного импульсов.
Наиболее просто удар моделируется падением конструкции с определенной высоты на жесткую платформу. Конструкцию представляют моделью механической системы с одной степенью свободы.
В результате удара возникает колебательное движение массы относительно положения равновесия, соответствующего статическому прогибу упругого элемента под действием силы тяжести (рис. 4.8). Движе-
126
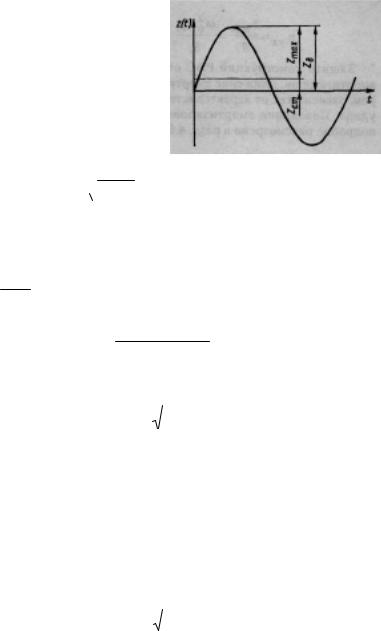
ние имеет характер свободных колебаний и без учета сил неупругого сопротивления протекает в соответствии с дифференциальным уравнением
mž + kz = 0. |
(4.10) |
Начальными условиями при этом являются:
при t = 0 z = -zCT , ż (0) = V0, где zCT = mg/K— статический прогиб
упругого элемента; v0 = 
 2gH0
2gH0
начальная скорость перемещения; Н0 — высота падения конструкции. Решение уравнения (4.10) для перемещения массы получают в виде
z(t) = (v0/(ω0)sinω0t-zCTcosω0t, |
(4.11) |
где ω0 = 
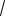 k / m — частота свободных колебаний. Из (4.11) можно найти максимальное перемещение массы
k / m — частота свободных колебаний. Из (4.11) можно найти максимальное перемещение массы
zmax = 
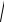 zCT2 + (v0 /ω0 )2
zCT2 + (v0 /ω0 )2
и полную (динамическую) деформацию упругого элемента
|
|
= z |
|
+ z |
|
= z |
|
(1+ |
|
|
)= μ z |
|
z |
Д |
CT |
max |
CT |
1+ v2 |
/ω 2 z2 |
CT . |
|||||
|
|
|
|
0 |
0 CT |
|
||||||
где µ— коэффициент динамичности конструкции.
Жесткость k и полная деформация упругого элемента определяют эквивалентную силу удара РУД =kzД =mgμ. При известной силе уда-
ра РУД можно найти напряжения, возникающие в упругом элементе конструкции.
Чтобы оценить перегрузки элементов при ударе, из соотношения
(4.11) находят ускорение
ž(t) = - V0 ω0 sin ω 0t + zCT ω20 cos ω0t.
Максимальное значение ускорения
×× |
|
|
|
|
|
( 1+ v2 |
/ω 2z2 |
) |
|||
zmax = ω 2 z |
|||||
0 CT |
0 |
0 CT |
|
||
определяет перегрузку при ударе:
127

|
∙ |
|
ω 2 z |
|
|
|
|
V ω |
||
|
zmax |
|
|
|
|
|
||||
η = |
= |
1+ V 2 |
/ω2 z2 |
≈ |
||||||
|
|
0 CT |
0 0 |
|||||||
|
|
|
||||||||
УД |
g |
|
|
g |
0 |
0 CT |
|
g |
||
|
|
|
|
|
|
|
||||
Защита конструкций РЭС от ударов осуществляется с помощью амортизаторов. Движение амортизированной системы, вызываемое ударом, зависит как от характеристик самой системы, так и от параметров удара. Поведение амортизированных систем при воздействии удара подробно рассмотрено в разд. 4.6.
4.3. Расчет показателей вибропрочности конструкций РЭС
Исходя из определения вибропрочности и анализа динамических процессов, протекающих в элементах конструкций РЭС при вибрациях, можно определить следующие условия обеспечения вибропрочности:
отсутствие в конструкции механических резонансов;
ограничение амплитуды виброперемещения и виброскорости значениями, исключающими опасные напряжения и усталостные явления в элементах конструкции;
допустимые значения виброперегрузок в диапазоне частот внешних воздействий должны превышать величины, определенные техническим заданием на разработку конструкции РЭС.
Первое условие выполняется, если частота свободных колебаний элементов конструкции лежит за пределами диапазона частот внешних
воздействий. |
Ввиду |
того, |
что |
частота |
свободных |
|
колебаний ω0 = |
|
, где k |
|
элемента конструкции; т — |
||
k / m |
— жесткость |
|||||
масса,для снижения массы конструкции приемлемым является решение: ω0>ωв где ωв верхняя граница диапазона частот внешних воздействий.
Проверка выполнения условия прочности конструкции при вибрации производится на основе приведения динамической задачи к статической [52]. Для этого необходимо найти коэффициент динамичности конструкции ц и нагрузку, которая возникает в элементах конструкции:
P = mgμnB,
где m — масса элемента конструкции; g — ускорение свободного падения; n B — вибрационная перегрузка элемента при резонансе. Затем по
формулам сопротивления материалов следует определить допустимое напряжение, которое может выдержать элемент в течение заданного срока эксплуатации:
128
σдоп=σ/n.
где σ — предельное значение напряжения (предел прочности) для материала; п — запас прочности.
Запас прочности обычно устанавливают на основе так называемого дифференциального метода в виде произведения частных коэффициентов:n=п1п2n3,гдеп1=1,2...1,5— коэффициент достоверности определения расчетных нагрузок и напряжений; п 2= 1,0... 1,5 — коэффициент, учитывающий степень ответственности детали; п 3 = 1,2... 3-коэффициент, учитывающий однородность механических свойств материалов.
Вслучае изгибных деформаций наряжение на изгиб
σи = М и / W и σ и д о п ,
где М и — изгибающий момент в наиболее опасном сечении элемента конструкции; Wи— момент сопротивления при изгибе.
Усталостные разрушения характерны для циклических нагрузок на высоких частотах вибраций и обычно наблюдаются при резонансных колебаниях радиоэлементов. Чаще всего разрушаются выводы радиоэлементов, так как механические напряжения в определенных сечениях выводов (область изгиба и соединения с контактными площадками коммутационных плат) при вибрациях на резонансной частоте резко возрастают. Если известно максимальное циклическое напряжение в выводах, то по кривой усталости для материала можно определить число циклов до разрушения и, таким образом, составить прогноз долговечности изделия. Количественной оценкой долговечности служит время работы элемента до разрушения выводов
tp=Np/f01.
Где Np — число циклов нагрузки до разрушения; f01— частота свободных колебаний основного тона элемента.
Связь между виброперегрузкой nв , частотой ω и амплитудой вибраций Z определяется выражением (4.2). Если исходя из допустимых напряжений, возникающих в материале элемента конструкции, положить ограничение на амплитуду вибраций, то получим предельное значение виброперегрузки:
nВ. ДОП ≤ |
ω 2Z |
ДОП |
(4.12) |
|
g |
||||
|
|
|||
|
|
|
129 |
|
Выразив виброперегрузку через виброскорость V, можно найти допустимое значение виброперегрузки при ограничении на виброскорость
nВ. ДОП ≤ |
ω VДОП |
|
g |
||
|
Условие вибропрочности конструкции выполняется, если
nв.доп≥nв.тз
Проверку неравенств (4.12) и (4.13) целесообразно проводить или на нижней частоте вынужденных колебаний или на резонансной частоте, где амплитуда вибраций и виброскорость достигают больших значений. Так, например, при низкочастотных вибрациях (f= 5 ... 50 Гц) для п в = 4 амплитуда вибраций лежит в пределах 40...0,4 мм и изгибные деформации могут вызвать разрушение элемента конструкции. На частоте вибраций 1000 Гц при прежнем значении виброперегрузки амплитуда вибраций Z = 1 мкм. Однако вследствие большого числа циклов колебаний могут возникнуть усталостные явления в материале.
Таким образом, оценка вибропрочности конструкций РЭС производится по следующим показателям:
частоте свободных колебаний ω0 ; допустимому значению напряжения σ доп в материале элементов
конструкции и предельному числу циклов нагружения N р; допустимому значению виброперегрузки п в доп .
При расчете частот свободных колебаний элементы конструкций РЭС заменяют эквивалентными расчетными моделями, для которых получены аналитические соотношения, связывающие частоту свободных колебаний с параметрами модели. Основным условием замены является соответствие модели реальной конструкции и минимальное число степеней свободы. Так как резонансные явления могут возникнуть на всех структурных уровнях конструкции, то желательно определять частоты свободных колебаний радиоэлементов, узлов, субблоков и т.д. При этом в зависимости от способа монтажа радиоэлементы могут заменяться расчетными моделями балки или рамы, в качестве расчетных моделей функциональных узлов и других планарных конструкций используется модель пластины.
4.3.1. Расчет частоты свободных колебаний радиоэлементов
Согласно [63] при конструировании узлов РЭС на печатных платах применяется ряд вариантов установки радиоэлементов. Воздействию
130
вибрации в большей степени подвержены |
|
||
радиоэлементы, |
установленные |
по |
|
вариан- |
|
|
|
там, не предусматривающим механического |
|
||
соединения корпуса с платой. Поэтому в |
|
||
первую очередь рассмотрим примеры по- |
|
||
строения расчетных моделей для таких |
|
||
радиоэлементов. |
|
|
|
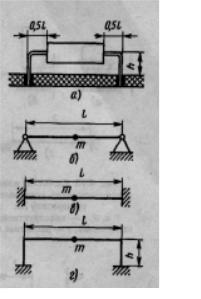
На рис. 4.9, а показана установка радио- |
|
||
элемента по варианту П. Расчетными |
|
||
моделями данной |
конструкции |
могут |
|
служить: балка с шарнирным или жестким |
|
||
закреплением на концах (рис. 4.9, б,в) и |
|
||
рама (рис. 4.9, г). Длины балки и |
|
||
горизонтальной связи рамы l определяются |
|
||
длиной выводов радиоэлемента от корпуса |
|
||
до изгиба. Корпус элемента моде- |
|
||
лируется сосредоточенной массой т. |
|
|
|
Транзистор и конденсатор, установлен- |
Рис. 4.9. Расчетные модели |
||
ные на плате по варианту ||В (рис. 4.10, а,б), |
|||
и радиоэлементы, установленные по вари- |
радиоэлемента, установлен- |
||
ного по варианту П: |
|||
анту III (рис. 4,10, в), заменяются расчетны- |
а —установка радиоэлемента |
||
ми моделями в виде балки, жестко закреп- |
на печатной плате; |
||
б, в — расчетные модели |
|||
ленной с одного конца, с сосредоточенной |
в виде балки; г — расчетная |
||
массой на свободном конце (рис. 4.10, г). |
модель в виде рамы |
||
Длина балки l равна длине выводов от пла- |
|
||
ты до корпуса радиоэлемента. |
|
|
|
Расчетной моделью радиоэлемента, смонтированного |
по |
варианту |
|
IV (рис. 4.11, |
а), является балка, жестко закрепленная с |
двух сторон |
|
(рис. 4.11,6). |
|
|
4,12, а,б), |
Если корпус |
радиоэлемента закрепляется на плате (рис. |
||
то анализ динамических процессов при вибрации может быть выполнен по расчетным моделям в виде рамы или арки (рис. 4.12, в,г).
В условиях внешних механических воздействий в элементах конструкций РЭС, приводимых к модели балки, возникают продольные, крутильные и изгибные колебания. Однако жесткость балки на изгиб, как правило, бывает ниже жесткости на растяжение и кручение. Поэтому для практики расчет изгибных колебаний представляет наибольший интерес.
Схема нагружения балки с шарнирным закреплением концов приведена на рис. 4.13, а, где приняты следующие обозначения: q = mž/l —
распределенная нагрузка балки, т — масса, ž— виброускорение, l — длина балки, z (x, t) — максимальный прогиб балки при вибрации. На
131
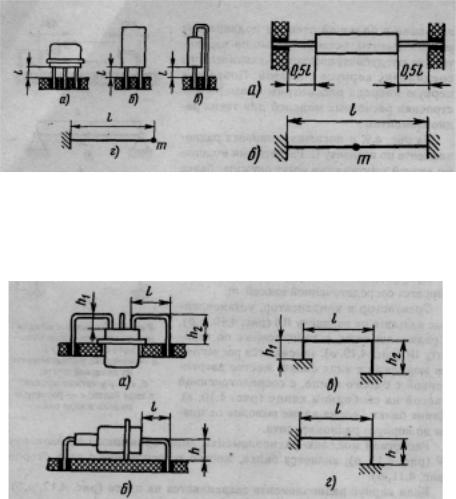
Рис. 4.10. Расчетная модель |
Рис. 4.11. Расчетная |
|
радиоэлементов, установленных |
модель |
|
повариантуШ: |
||
радиоэлемента, установленного |
||
а, б, в — конструктивные |
||
по варианту IV: |
||
исполнения; г — расчетная |
о.—/установкарадиоэлемента; |
|
модель |
б — расчетная модель |
|
|
Рис. 4.12. Расчетные модели радиоэлементов, установленных по варианту V: а, б—установкарадиоэлементовнапечатнойплате; в,г—расчетныемодели
рис. 4.13, б показаны возможные формы колебаний, которые характери зуются числом полуволн п , укладывающихся на длине балки.
При расчете частоты свободных колебаний балки принимают следу ющие допущения:
упругая ось балки совпадает с линией центров масс поперечных сечений;
при колебаниях все точки балки смещаются перпендикулярно первоначальному направлению оси;
все поперечные сечения балки остаются плоскими.
132
