Работа №4 Часть 1.Системы дифференциальных уравнений. Дифференциальные уравнения высших порядков
Системы дифференциальных уравнений n-го порядка решаются аналогично одному уравнению. Разница заключается в том, что n начальных условий и n правых частей записываются в матрицу-столбец n-го порядка. Результатом является матрица, содержащая n + 1 столбец: 0-й столбец – как всегда аргумент, с 1-го по n + 1-й – искомые функции.
Например, решить систему обыкновенных дифференциальных уравнений 2-го порядка
с
начальными условиями x0(0)
= 0; x1(0)
= 1 в 100 точках на интервале t
при
= –0,2 .
Здесь аргументом является t, искомыми функциями х0(t) и х1(t).
Параметр задается до его использования.
На рис. 23 показано решение поставленной задачи с графиками полученных функций х0(t) их1(t), построенных в первых 30-ти точках.
Рис. 23
Задание 1. Разберитесь самостоятельно в приведенном примере и воспроизведите его в пакете MathCad.
Задание 2. Самостоятельно решить систему дифференциальных уравнений 3-го порядка
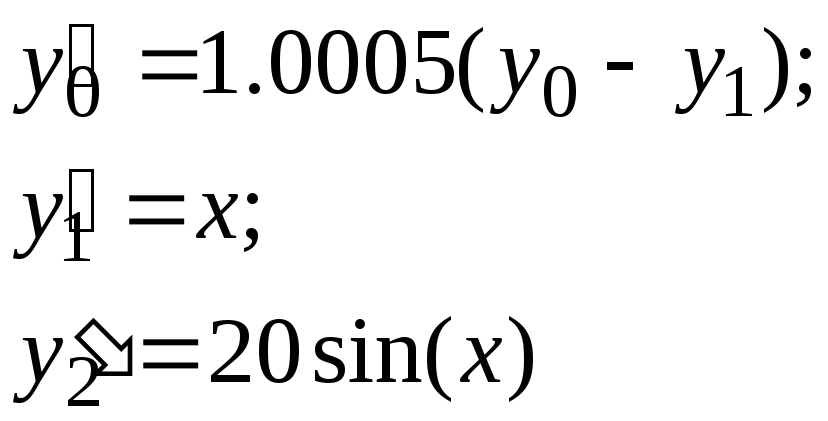
с начальными условиями у0(0) = 1; у1(0) = 0; у2(0) = 0,5 на интервале х(0; 10) в 50-ти точках. Построить графики функций у0(х), у1(х), у2(х) на одном поле. Перекрасить график функции у2(х) в черный цвет. Показать координатные линии – по 4 интервала на каждой оси.
Дифференциальные уравнения более высоких порядков сводятся к системе уравнений 1-го порядка. Для этого нужно сделать замену переменных. Замен нужно сделать столько, каков порядок исходного уравнения.
Пусть требуется решить дифференциальное уравнение n-го порядка
an y(n) + an-1 y(n-1) + … + a2 y" + a1 y' + a0 y = b f(x)
с начальными условиями y(0) =c0;y'(0) =c1;y"(0) =c2; …y(n-1)(0) = cn-1.
Обозначим через g0функциюу, входящую в уравнение. Все ее производные с 1-й доn–1-ую включительно обозначим черезg1,g2, …gn-1и возьмем производные от обеих частей каждой такой замены с учетом того, что производные от функцииуобозначены буквойgс соответствующими индексами:
g0 = y; g0' = y' = g1;
g1 = y'; g1" = y" = g2;
g2 = y"; g2'" = y'" = g3;
: :
gn-1
= y(n-1); 
=y(n)
= h f(x)
– dn-1
y(n-1)
– … – d2
y" – d1
y' – d0
y. В последнем
равенствеn-ю производную
отуберем из исходного уравнения,
преобразовав его таким образом, чтобы
в левой части исходного уравнения
осталась старшая производная без
коэффициента. Все остальные члены
уравнения перенесены в правую часть с
коэффициентамh,di,
гдеi= 0,…,n
– 1;
Исходные данные преобразуются к следующему виду:
g1(0) = c0; g2(0) = c1; g2(0) = c2; … gn-1(0) = cn-1.
Таким образом, имеем систему nдифференциальных уравнений 1-го порядка, аргументом в которой по-прежнему являетсях, а искомыми функциями сталиg0(х),g1(х),g2(х), …gn-1(х):
Как решить такую систему дифференциальных уравнений Вы уже знаете.
Задание 3. Решить дифференциальное уравнение 2-го порядка y" + y' – 2y = 0 с начальными условиями y(0) = 1; y'(0) = 3 на интервале x(0; 0,5) в 50-ти точках.
Чтобы
решить это дифференциальное уравнение
2-го порядка, нужно заменой переменных
привести его к системе 2-х уравнений
1-го порядка:
Теперь возьмем производные от каждого
из этих равенств:g'0
= y'
= g1;
g'1
= y"
= –y'
+ 2y
= –g1
+ 2g0.
Получили 2 уравнения 1-го порядка:
Решаем полученную систему методом Рунге-Кутта.
На рис. 24 приведено решение этой системы. Результатом является матрица z, содержащая 3 столбца. В нулевом столбце – аргумент, в первом – искомая функцияу, во втором – ее производнаяу'. Построены графикиуиу'.
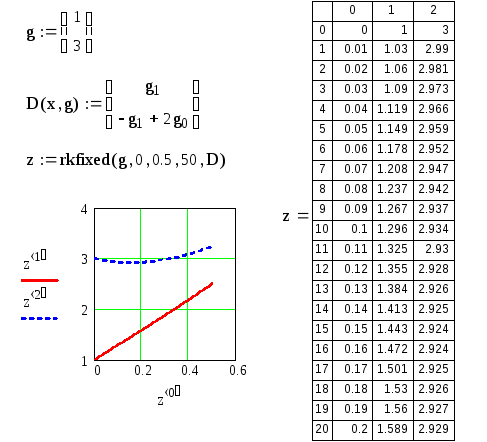
Рис. 24
Задание 4. Самостоятельно решить систему дифференциальных уравнений 4-го порядка y"" – 2k2y" + k4y = 0 в 50-ти точках на интервале х (0; 5) с начальными условиями y(0) = 0; y'(0) = 1; y"(0) = 2; y'"(0) = 3 при k = 3.
Построить графики у(х), у'(x), y"(x), y'"(x) на одном поле. Поле растянуть на ширину страницы. Изменить левую границу интервала по оси х на 3,5. Заменить тип линий: 1– bar (брусок); 2 – draw (черточка); 3 – step (ступенька); 4 – points (точки), symbol – o's (точки в виде кружочков). Сделать вес каждой кривой – 2 (в два раза толще).