Часть 2.Дифференцирование функций. Решение дифференциальных уравнений

Для определения производной какой-либо функции необходимо поставить значок (см. рис. (20), набрать функцию,выделить все выражение и произвести символьное преобразование.

Задание 1. Взять производную от функции .

Для численного дифференцирования нужно перед производной задать значение аргумента, при котором хотим узнать значение производной от функции, набрать знак производной, саму функцию и затем нажать знак равенства.

Задание 1. Определить значение производной функции у(х) = х² + х – 1 при х = 1:

x:=1 =

Задание 2. Самостоятельно найти производную функции f(x) = 6x⁵ + 3x² и определить ее значение в точке x = 2,5 .

Аналогично можно найти вторую, третью и т.д. производные, только значок нужно поставить (см. рис. 20). Степень производной заполняется только в знаменателе этой дроби,в числителе MathCad поставит сам.

Задание 3. Определить значение второй, третьей и четвертой производных функции у(х) = х³ + 5 в точке х = 2,5. (Значение х можно присвоить один раз, если оно постоянно).

Решить дифференциальное уравнение – это значит найти функцию y(x), удовлетворяющую начальным условиям. MathCad решает дифференциальные уравнения численными методами, то есть находит значение искомой функции в дискретных точках заданного интервала. Ответом будет являться матрица значений аргумента х и функции y в этих точках. MathCad обладает несколькими численными методами решения дифференциальных уравнений. Один из них – метод Рунге-Кутта с фиксированным шагом – работает при использовании встроенной функции rkfixed. Чтобы воспользоваться этой функцией, необходимо преобразовать исходное уравнений таким образом, чтобы в левой части осталась производная без коэффициента, а все остальные члены уравнения были перенесены в правую часть. На экране должно быть записано начальное условие, присвоенное переменной у. Затем надо правую часть заданного уравнения присвоить любому идентификатору с параметрами х и у. Затем какой-либо переменной присвоить обращение к функции rkfixed. Аргументами функции rkfixed являются переменная, обозначающая искомую функцию, интервал изменения аргумента, количество точек, в которых ищется функция у(х), правые части. На рис. 21 приведено решение дифференциального уравнения y' + 3y = 0 в 50-ти точках с начальным условием у(0) = 4 на интервале х(0; 2).

Уравнение преобразовано к виду y' = –3y.

Начальное условие

Правая часть

Обращение к функции

График у(х)

Результат решения

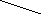
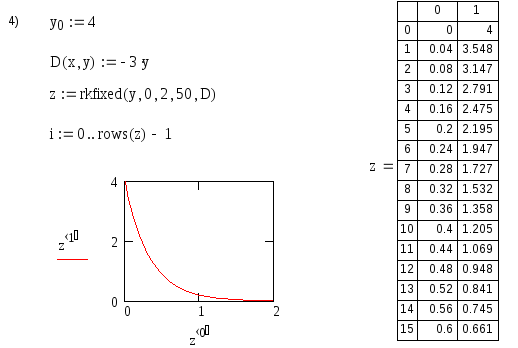
Рис. 21

Начальные условия записаны в виде y:= 4.

Правая часть уравнения (–3y) присвоена идентификатору D с параметрами, первый из которых – аргумент (в нашем случае х), второй – функция (для нашего примера – у): D(x, y):= –3y. Результат выполнения функции rkfixed присвоен переменной z. Аргументами функции rkfixed являются переменная у, интервал изменения переменной х (0, 2), количество точек, в которых ищется решение (50), функция правой части исходного уравнения (D) (Рис. 22).

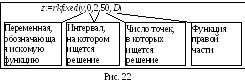
Решением дифференциального уравнения является матрица z, в нулевом столбце которой всегда находится аргумент (в нашем случае х), в первом столбце всегда – искомая функция (в нашем примере – у). Чтобы увидеть решение, необходимо записать z = .

На рис. 21 результат решения (т.е. матрица z) показан в виде таблицы чисел. Таблица имеет столько строк, в скольких точках найдено решение. В нашем примере это 50 точек. Чтобы посмотреть все 50 точек, нужно воспользоваться линейкой прокрутки, которая появляется справа от таблицы, если щелкнуть по ней мышкой. Как видим, в нулевой строке матрицы z стоят числа 0 и 4, т.е. при х = 0 у = 4, что соответствует заданному начальному условию.

Чтобы построить график найденной функции y(x), нужно вспомнить, что аргумент х хранится в нулевом столбце матрицы z, а функция у – в первом столбце этой матрицы. Для обозначения нужного столбца какой-либо матрицы существует кнопка М^{< >} (см. рис. 9, а). В треугольных скобках пишется номер нужного столбца. На рис. 21 показан график зависимости первого столбца матрицы z от нулевого столбца, т.е. зависимость у от х.

Если мы хотим построить график не во всем заданном интервале аргумента, т.е. не во всех точках, необходимо задать до графика интервалы изменения первого индекса матрицы z (номер строки). Номер нужного столбца набрать как второй индекс матрицы z. Например, чтобы построить график функции у(х) с 5-й по 25-ю точки, нужно записать

i:=5..25

z_i,1

z_i,0

Задание 4. Самостоятельно решить дифференциальное уравнение y' + y² – x = 0 с начальными условиями y(0) = 1 на интервале х(0; 10) в 50-ти точках методом Рунге-Кутта с фиксированным шагом. Построить график функции у(х) во всех 50-ти точках.

Задание 5. Самостоятельно решить дифференциальное уравнение y' = sin(x) – 1 с начальными условиями у(0) = 0 в 100 точках интервала х(0; 10). Построить график функции у(х) с 5-й по 60-ю точки.