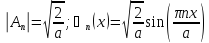36. Вероятностный характер волн де Бройля.

|A|^2 – плотность вероятности нахождения частицы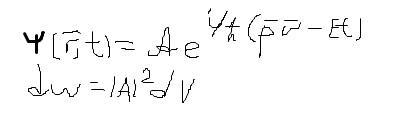

dW –вероятность нахождения частицы в данной точке пространства

Опыт по дифракции при очень малой интенсивности

Через год подобрали интенсивность так

Электрон пролетает через тонкую фольгу

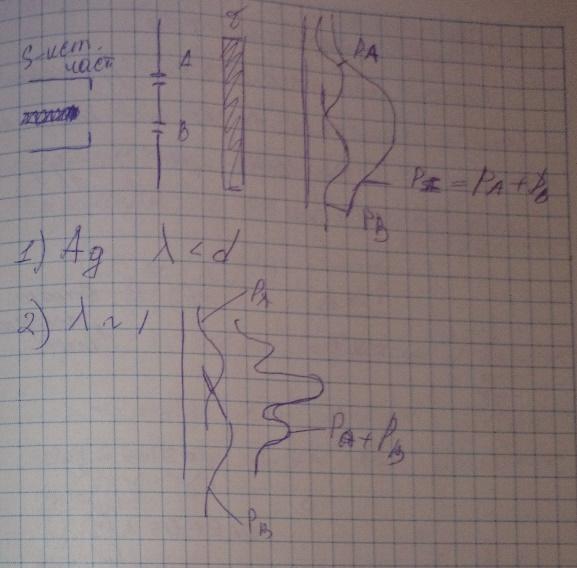
Всякая попытка узнать что-либо о свойствах микрочастиц обязательно меняет их состояние и волновую функцию

37. Принцип неопределенности Гейзенберга. (лекция 10)

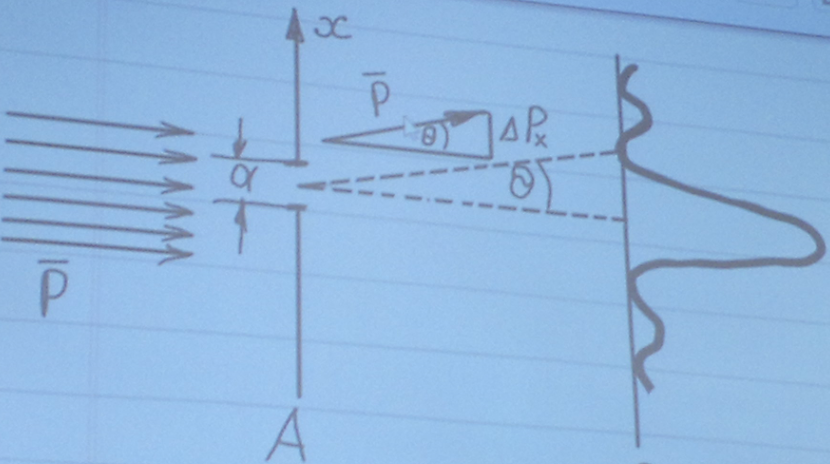
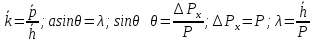
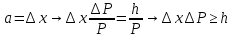
Также можно связать энергию и время:

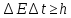
Если принять Δt за время жизни электрона в некотором состоянии, то получится, что оно связано с неопределенностью в энергии.

Общая формулировка соотношения неопределенностей выглядит так:

Произведение неопределенностей двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка.

38. Оценки характеристик микрочастиц с помощью соотношения неопределенностей. (лек 10)

Соотношение неопределенностей получить правильный порядок физических величин.

1. Оценка размеров атома водорода

P = h̅ / a, где а – среднее расстояние от электрона до ядра в атоме водорода, P – разброс в импульсах. Расстояние «а» определяет условие минимума полной энергии электрона в атоме:

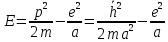
Определим минимум энергии:

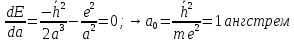
2. На примере движения электронов в электронно лучевой трубке покажем с какой степенью точности можно говорить о траектории микрочастиц в определенных условиях. Оценим неопределенности координат и импульса.

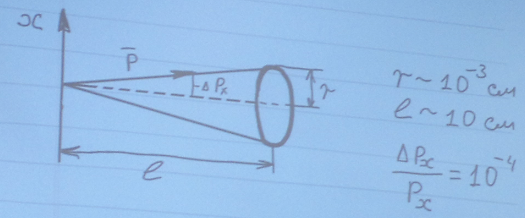
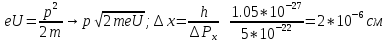
Получается, что электрон движется почти по траектории.

Для макротел значения неопределенностей не существенны и ими можно пренебречь.

39. Уравнение Шредингера.

Движение любой микрочастицы можно описать волновой функцией или пси-функцией, как было предложено де Бройлем для свободной частицы. Если частица не является свободной, а находится в некотором потенциальном поле, то чтобы определить стационарное состояние частицы и ее энергетический спектр, необходимо решить уравнение Шредингера.

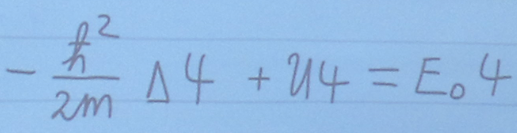- это уравнение Шредингера для стационарных состояний

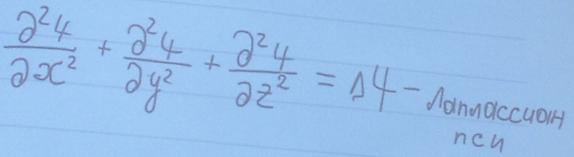
Пси-функция должна быть конечной, непрерывной и однозначной. Частные производные от пси-функции должны быть непрерывны. Пси-функция должна быть суммируема с квадратом (условие нормировки):

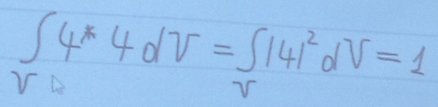
Плотность вероятности обнаружить частицу в объеме V равна 1.

Уравнение Шредингера со временем:

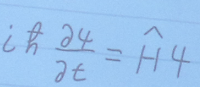
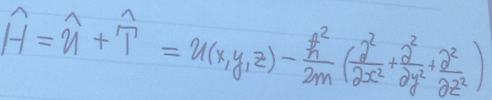
H – оператор полной энергии, который является суммой операторов потенциальной и кинетической энергии.

40. Простейшие задачи квантовой механики (потенциальная яма с бесконечно высокими стенками) (лекция 11).

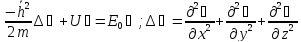
В одномерном случае: 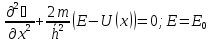, где U(x) – потенциальная функция.

Рассмотрим самый простой случай - потенциальная функция соответствует потенциальной яме с бесконечно высокими стенками. Потенциальная функция:(рис 1)

Естественными граничными условиями для такой ямы будут равенства:

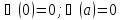
Для промежутка 0<X<a уравнения (2) запишется в виде:

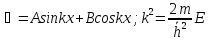
Первое из граничных условий сразу дает B = 0, второе приводит к соотношению:

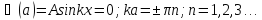
(n = 0 – отпадает, поскольку при этом получается, что пси-функция тождественно нулю, т.е. частицы нигде не находится.)

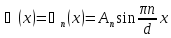
Исключив k (6) и (8), найдем собственные значение энергии частицы:

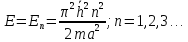
Итак, энергия частица в потенциальной яме может принимать только дискетные значения! Если частица локализована в пространстве в ограниченной области, то спектр значений энергии частицы дискретен, при отсутствии локализации – спектр энергий непрерывен.

(рис 2)Оценим расстояние между соседними уровнями для различных значений массы частицы “m” и ширины ямы “a”. Разность энергий двух соседних уровней равна:

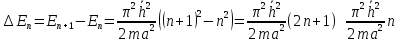
Молекула газа в сосуде:

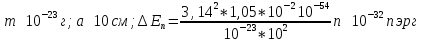
Столь густо расположенные энергетические уровни будут восприниматься как сплошной спектр энергии, хотя квантования будет иметь место, но на характере движения молекул сказываться не будет.

Свободный электрон в металле: 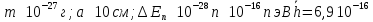Эв*с

Это также очень маленькая дискретность, которая не скажется на энергетическом спектре и на характере движения электрона.

3) Электрон, локализованный в области атомных размеров:

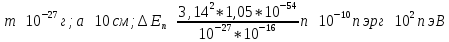
Амплитуда волновой функции в (9) – “An” из условия нормировки :
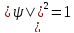