Полиномиальные уравнения

Полиномиальным уравнением называется уравнение , где– неизвестные полиномы от переменногоx, левая часть этого уравнения должна быть равна нулю при всех значениях переменного x.

Из полиномиальных уравнений мы рассмотрим только простейшее линейное полиномиальное уравнение с двумя неизвестными многочленами:

, (5)

где ,,– известные многочлены,,– многочлены, которые нужно найти, равенство (5) должно выполняться при всех значениях переменногоx.

Решения такого полиномиального уравнения определяются неоднозначно. Так как уравнение линейное, то его общее решение строится так же, как и решение любого линейного уравнения или системы уравнений (системы алгебраических линейных уравнений, дифференциальные линейные уравнения и т.п.). Общее решение полиномиального уравнения (5) имеет вид ,, где,– какое-нибудь одно решение (частное решение) уравнения (5);,– общее решение соответствующего однородного полиномиального уравнения

. (6)

Если полиномы ,имеют наибольший общий делитель, который не является делителем, то уравнение (5) не имеет решений.

Если наибольший общий делитель ,является делителем, то обе части уравнения (5) делят на этот делитель, а затем решают получившееся уравнение.

Если многочлены ,взаимно простые, то уравнение (5) всегда имеет решение.

Если многочлены ,взаимно простые, то общее решение уравнения (6) имеет вид,, где– произвольный многочлен.

Если степень многочлена меньше суммы степеней многочленови, то уравнение (5) называют правильным. Решение правильного уравнения, удовлетворяющее условиям,, называют минимальным решением.

Доказано, что если многочлены ,взаимно простые, то у правильного уравнения (5) минимальное решение всегда существует и притом только одно.

Пусть ,. Чтобы найти минимальное решение, нужно записатьис неопределенными коэффициентами:

,

,

подставить их в (5), выполнить умножения слева и приравнять коэффициенты при одинаковых степенях x справа и слева. В результате получим линейную систему уравнений для неизвестных ,. Решив ее, можем записать минимальное решение. Если многочлены,имеют близкие корни, то эта система будет плохо обусловлена.

Рассмотрим случай, когда уравнение (5) является неправильным, т.е. . Представимв виде, где– остаток от деленияна произведение. В итоге получим, что. Неизвестный многочленбудем искать в виде. Подставив это выражение в (5), получим

Откуда . Это уравнение является правильным уравнением с неизвестнымии. Как его решать, мы уже выяснили выше.

Вычисление интегралов

Для вычисления определенного интеграла имеется много различных численных методов. Какой выбрать, зависит от того, насколько гладкой является функция, как дорого обходится ее вычисление и с какой точностью нужно получить результат. В этом пособии рассматривается только группа методов, использующих формулы Ньютона – Котеса. В этих методах предполагается, что нет ограничений на то, сколько раз придется вычислять, и что известно, сколько раз дифференцируема функция.

Во всех этих методах отрезок интегрирования разбивается на n равных частей с шагом h. Точки (узлы) разбиения обозначим ,,,. Обозначим,. Приведем несколько наиболее известных формул для приближенного вычисления интегралов, в нихJ – приближенное значение интеграла.

1. Левая формула прямоугольников .

2. Правая формула прямоугольников .

3. Центральная формула прямоугольников .

4. Метод трапеций .

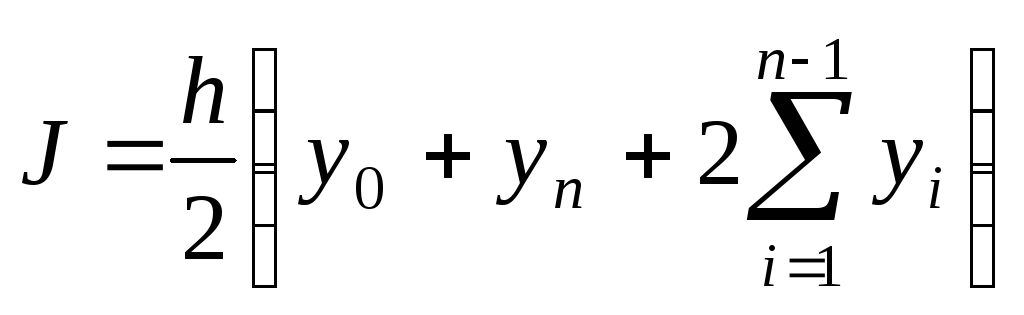5. Метод Симпсона . Заметим, что в первой сумме в этой формуле суммируютсяс четными номерами (кроме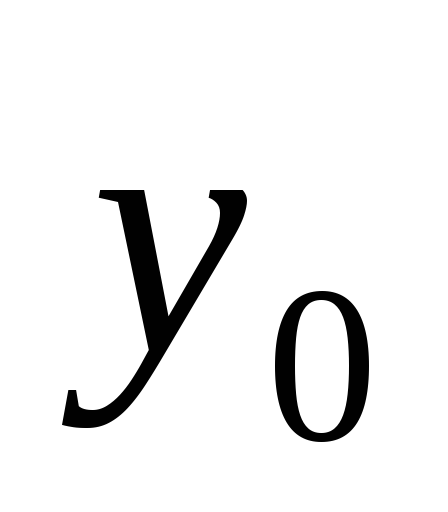и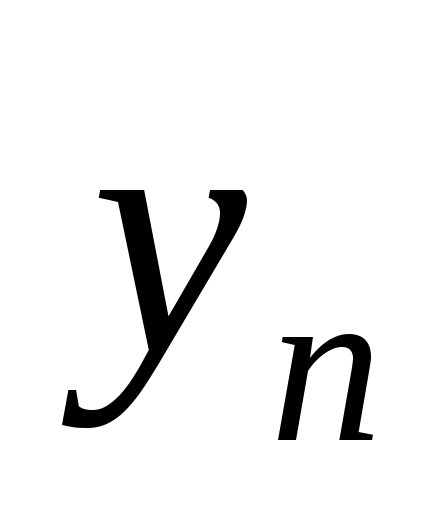), во второй сумме – с нечетными. В этой формуле число отрезков разбиенияn всегда обязано быть четным.

Рассмотрим преимущества и недостатки этих формул. Главное – это оценка точности. Пусть I – точное значение исходного интеграла. Тогда величина ошибки | I – J | оценивается так:

1. Для формул 1, 2 , т.е. эти формулы имеют первый порядок точности.

2. Для формул 3, 4 , второй порядок точности.

3. Для формулы Симпсона , четвертый порядок точности.

В приведенных оценках h – это шаг интегрирования, константа C зависит от интегрируемой функции и не зависит от величины шага интегрирования. Для величины константы C существуют формулы, в которых участвуют производные интегрируемой функции, при желании вы можете найти их в учебниках и справочниках. Однако эти формулы имеют скорее чисто теоретическое значение, для реальных вычислений их использовать, как правило, не удается. Порядок точности означает следующее. Если вы уменьшаете шаг интегрирования в два раза, т.е. увеличиваете объем вычислительной работы тоже в два раза, то для первого порядка точности оценка ошибки уменьшается в два раза, для второго порядка – уменьшается в четыре раза, для четвертого – в 16 раз! На основании этого можно предположить, что наиболее выгодной является формула Симпсона. И, на самом деле, она является наиболее употребительной. Но если функция является негладкой, т.е. имеет очень большие производные или вообще их не имеет, то формулы второго и четвертого порядка точности могут давать значительно более плохие оценки ошибки за счет резкого увеличения константы C. Так в формуле Симпсона для оценки ошибки используется максимальное значение модуля четвертой производной интегрируемой функции. Поэтому для заведомо негладких функций следует использовать формулы прямоугольников.

Для оценки ошибки при реальном вычислении интегралов используется обычно правило Рунге. Пусть применяется метод порядка k. Вычисляется приближенное значение интеграла с шагом h, обозначим его , и значение интеграла с шагом 0,5h, обозначим его . Тогда считается, что ошибка последнего результата не превосходит, т.е.. Использование такой оценки не дает стопроцентной гарантии достижения заданной точности. Однако для гладких функций, используемых в инженерных расчетах, она дает вполне удовлетворительные результаты. Для негладких функций, особенно разрывных, правило Рунге применять нельзя.

В системе MATHCAD по умолчанию автоматически выбирается наиболее подходящий метод интегрирования. Один из них – метод Ромберга. Его формулировка достаточно сложная. Суть заключается в следующем. Производится ряд вычислений интеграла по формуле Ньютона-Котеса. При каждом следующем счете число отрезков разбиения удваивается и, кроме того, повышается порядок метода. Ошибка оценивается по правилу Рунге. Как только она оказывается меньше заданной точности, вычисления прекращаются.