Вычисление определенных интегралов

Вычисление определенного интеграла в системе МС предельно просто. Для этого достаточно вызвать шаблон определенного интеграла с панели Calculus и заполнить шаблоны данных. Под знаком интеграла можно использовать и функции пользователя. Например,

, ,

.

Как видим, допустимо вычисление и несобственного интеграла.

Можно найти интеграл и от разрывных функций, например, возьмем функцию . Здесь использована функция if. Ее первым аргументом служит условие, вторым аргументом – формула, по которой нужно вычислять результат при выполнении указанного условия, третьим аргументом – формула, по которой вычисляется результат, если условие не выполнено. Чтобы убедиться, что функция разрывная, начертим ее график при a = 1 (рис. 26). Вычислим интеграл

.

Точность вычисления интегралов регулируется системной переменной TOL.

В большинстве задач никаких неприятностей при вычислении интегралов не возникает. Но если функция быстро меняется на отрезке или имеет слишком много разрывов, то система может не выдать ответа или ответ будет иметь меньшую точность, чем указано в переменной TOL. Для иллюстрации возьмем функцию . Здесьfloor(x) – это целая часть числа x. Функция равна дробной части числаx, тому, что получится, если отбросить цифры до десятичной точки. График функции F(x) приведен на рис. 27. Эта функция является периодической с периодом 1. Возьмем функцию . Это такая же функция, только ее период равен. Пусть, тогда. Если же, то система отказывается вычислить интеграл.

Для некоторых функций возможно символьное вычисление определенного интеграла по формуле Ньютона – Лейбница:

, .

Решение дифференциальных уравнений

Для решения обыкновенных дифференциальных уравнений в системе МС имеется несколько функций. Их можно вызвать, нажав кнопку f(x) на панели инструментов и в развернувшемся списке слева выбрав Differential Equation Solving. После этого в развернувшемся списке справа нужно выбрать требуемую функцию. Мы рассмотрим лишь некоторые из них. Функции Rkadapt, rkfixed используют метод Рунге–Кутты, функции Bulstoer, Stiffb используют метод Булирша–Штёра, функция Stiffr – метод Розенброка. Эти функции дают решение на равномерной решетке узлов интегрирования. Их можно использовать как для решения одного уравнения, так и для решения системы дифференциальных уравнений.

Система МС14 поддерживает также функции, возвращающие значения решений на неравномерной сетке узлов, которые использовались в предыдущих версиях системы МС, хотя и не включает их в свой список функций. Эти функции имеют такие же имена, но начинаются эти имена не большой, а строчной буквой. Списки аргументов у них другие.

Кроме перечисленных, имеется еще функция Odesolve, которая предназначена для решения дифференциальных уравнений, причем порядок уравнений может быть бόльшим единицы. Использование функции Odesolve резко отличается от использования других функций и будет описано позже.

Для использования функций МС дифференциальное уравнение или система дифференциальных уравнений предварительно должны быть записаны (на бумаге, а не на экране) в виде

.

Пусть требуется найти решение этого уравнения с начальным условием на отрезке. Это равенство на экране тоже писать не нужно! Для решения задачи создаем в МС функцию пользователя. ВНИМАНИЕ, первым пишется независимый аргумент, вторым – искомое решение, аргументов ОБЯЗАТЕЛЬНО должно быть ДВА, не больше и не меньше. Первый аргумент указывается даже в том случае, если в уравнении переменноеx в явном виде отсутствует (оно обязательно присутствует, скрыто, в символе дифференцирования). Дальнейшие действия разберем на примере применения функции Rkadapt.

Пусть требуется решить задачу Коши для уравнения с начальным условиемна отрезке [0.5; 4]. В соответствии со сказанным выше уравнение переписываем (на бумаге) в виде. Создадим функцию. Теперь применим функциюRkadapt. Ее первым аргументом является значение решения в начальной точке, вторым – левая граница отрезка интегрирования, третьим – правая граница отрезка интегрирования, четвертым – число узлов, выводимых на экран, пятым – имя функции, без указания аргументов. Результатом служит матрица, где первый столбец – это значения независимого аргумента, второй столбец – значения решения при этих значениях аргумента. Если решается система уравнений, то второй столбец дает значения первой компоненты решения, третий столбец – значения второй компоненты решения и т.д. Итак, . Для экономии места матрицы будут приводиться в виде рисунков. Посмотрим матрицу значений решения, рис.28. Видим, что в матрице показаны не все заказанные узлы,x изменяется только до 3.125. Это связано с принятым в МС правилом вывода матриц на экран. Чтобы увидеть остальные узлы, нужно щелкнуть мышью на блоке матрицы. Появится полоса прокрутки, с помощью которой можно просмотреть остальные значения.

Интересно выяснить, насколько полученные результаты отличаются от точного решения. В данном примере уравнение взято специально такое, что можно получить формулу точного решения. Это делает бессмысленным выполненное численное интегрирование, но позволяет сравнить точное и приближенное решения. Исходное уравнение – линейное, его решение с заданными начальными условиями таково:

.

Создадим соответствующую функцию вMATHCAD (самостоятельно). После этого создадим так называемую ранжированную переменную (две точки набираются или нажатием клавиши ; на клавиатуре, или клавишиm..n на панели Calculator). Эта запись означает, что переменная k пробегает значения от 0 до 20 с шагом 1. Создадим матрицу S значений точного решения в тех же узлах, где было получено приближенное решение. Образуем первый столбец новой матрицы S, в котором будут указаны узлы интегрирования, . Второй столбец составим из значений точного решения в этих узлах. Посмотрим матрицу значений точного решения, рис. 29.

Сравнив матрицы S и Z (для удобства нужно матрицу Z перетащить и поставить рядом с матрицей S), видим, что значения с точностью до 0.001 совпадают, это соответствует значению переменной TOL, равной по умолчанию 0.001. Переменная TOL определяет для системы МС шаг интегрирования и поэтому отвечает за точность приближенного решения. Если число знаков после запятой при выводе на экран увеличить до 9, то в последних узлах интегрирования возникнет отличие точного решения от приближенного. Таким образом, система проинтегрировала это уравнение со значительно более высокой точностью, чем установленная по умолчанию.

Рассмотрим функцию rkfixed. Ее аргументы такие же, как у функции Rkadapt. Ее отличие от Rkadapt заключается в том, что система выполняет ровно столько шагов интегрирования, сколько указано в четвертом аргументе, не беспокоясь о точности вычисляемого решения. Предполагается, что пользователь сам определил число узлов в соответствии с точностью вычислений. При равном числе узлов это обеспечивает выигрыш в скорости по сравнению с функцией Rkadapt.

Применим функцию rkfixed к нашей конкретной задаче:

.

Результат приведен на рис. 30. Проверкой по точному решению убеждаемся, что в последней точке значение приближенного решения чуть-чуть отличается от точного.

Рассмотрим функцию Bulstoer. Ее действие полностью аналогично действию Rkadapt, только используется другой алгоритм,

,

результаты на рис.31. Как видим, полученные значения такие же, как и у точного решения.

Для демонстрации того, что не все обстоит так благополучно, как в предыдущем примере, увеличим отрезок интегрирования. Возьмем отрезок [0.5; 30]. На экране для этого достаточно исправить только один аргумент в каждой из функций. На бумаге приходится печатать все заново:

, ,.

Чтобы не тратить место на странице на вывод всех четырех

матриц, укажем только полученные значения приближенного решения в последней точке отрезка: 4.88638, 4.05668, 4.87236. Получим также значение точного решения в этой точке:. Сравнивая результаты, получаем, что в конечной точке все приближенные решения отличаются от точного. Наилучший результат дала функцияBulstoer, наихудший – функция rkfixed. Последнее следовало ожидать, так как пользователь, то есть мы, никак не согласовывали число шагов с желаемой точностью.

Стоит заметить, что ошибки во всех приведенных примерах, кроме rkfixed, малы и вряд ли могут быть существенны для инженерных расчетов. В то же время ошибки вычислений превышают допустимую ошибку, установленную по умолчанию TOL = 0.001.

Рассмотрим теперь уравнение, у которого не удается найти точное решение в аналитическом виде. Пусть требуется решить задачу Коши для уравнения с начальным условиемна отрезке [0; 3] и построить график этого решения.

Воспользуемся функциейRkadapt. Создадим функцию, являющуюся правой частью нашего уравнения . Число узлов интегрирования возьмем равным 15,, результат на рис. 32.

Чтобы проверить, с какой точностью найдено решение, изменим значение системной переменной TOL и снова найдем это решение. Для этого ниже полученной матрицы Y выполним оператор . После этого снова найдем решение, но обозначим его иначе:

. Чтобы не сверять пятнадцать пар чисел, облегчим себе задачу следующим образом. Возьмем два вектора и, являющиеся столбцами значений первого и второго решений (угловые скобки можно взять с панелиMatrix). Найдем модуль разности этих векторов: . Он

показывает, на сколько различаются решения. Видим, что расхождение имеет порядок 0.001. Так как второе решение ближе к точному, то естественно предположить, что первое отличается от точного тоже на величину порядка . Для инженерных расчетов это, как правило, приемлемая точность.

Построим график. Система МС умеет строить график не только по заданной функции, но и по таблицам значений аргумента и функции. График приведен на рис. 33.

График получился не гладким. Это значит, что число узлов для построения графика мало. Увеличим число узлов. На экране это можно сделать, исправив один из аргументов в формуле для матрицы Y, но при этом придется удалить вычисление разности первого и второго решения (разные размерности): . График представлен на рис. 34.

Теперь график выглядит более гладко и может считаться приемлемым для ответа к задаче. При необходимости таблицу значений можно вывести в файл в кодахASCII. Для этого служит функция WRITEPRN(■), где аргументом является имя файла (вместе с указанием пути к нему). Это имя набирается в кавычках, что является признаком строковой переменной. После этой функции ставится знак присвоения := и указывается имя выводимой матрицы. Полученный файл можно прочитать, например, в WORD или в любом другом редакторе.

Рассмотрим функцию Odesolve для решения дифференциальных уравнений. Эта функция предназначена для решения дифференциального уравнения или системы дифференциальных уравнений, в которые могут входить производные неизвестных функций второго и более высоких порядков. Единственное ограничение – производные наиболее высокого порядка должны входить в уравнения линейно. В этой лабораторной работе познакомимся с применением Odesolve к одному дифференциальному уравнению.

Следует отметить, что в различных версиях МС эта функция обладает разными особенностями. Приведенное далее изложение соответствует версии МС14. Такое же обращение с Odesolve в более ранних версиях МС может вызвать отказ системы дать ответ или вызвать появление неверного результата.

Функция Odesolve работает в блоке, начинающемся директивой given. Главное отличие функции Odesolve от функций, рассмотренных ранее, заключается в том, что в качестве результата мы получаем функцию как объект MATHCAD. Ранее мы получали матрицы. Для этих матриц мы могли получить значение решения только в узлах интегрирования. Используя функцию Odesolve, мы можем получить значение решения в любой точке отрезка интегрирования. Не нужно думать, что эта функция использует какой-то новый способ интегрирования дифференциальных уравнений. Она так же получает значения решения в узлах интегрирования, как было в методах, рассмотренных ранее, но кроме этого она по этим значениям строит функции для расчета в промежуточных точках (выполняет интерполяцию).

Для использования функции записываем директиву given. Затем ниже пишем само дифференциальное уравнение. При этом обязательно нужно помнить следующее:

1. знак = в уравнении набирается с панели Boolean (жирный);

2. неизвестная функция набирается с указанием аргумента. Например, не y, а y(x), не z, а z(x);

3. символ производной набирается, как ‘ левой верхней кнопкой на клавиатуре или Ctrl+F7, штрих ставится после имени функции. Например, 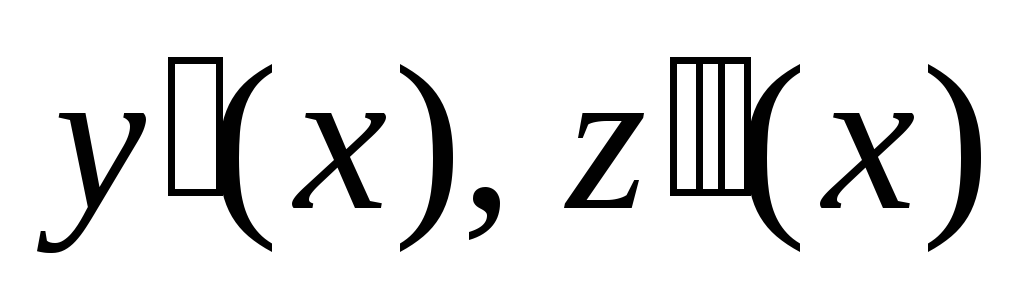. Можно использовать символы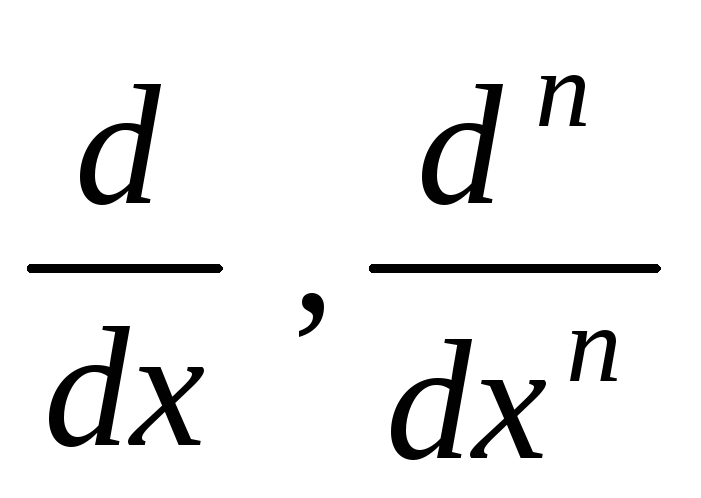с панелиCalculus.

После записи уравнения записываются начальные условия в виде ,. Знак = берется с панелиBoolean. После этого применяется функция Odesolve. Справа пишется имя, которым будет называться функция, являющаяся решением дифференциального уравнения. Аргумент после имени не указывется. Затем пишется знак присваивания, потом функция Odesolve. Первым аргументом функции Odesolve является имя независимой переменной, вторым – конечная точка отрезка интегрирования. Третий аргумент является необязательным, он равен числу узлов интегрирования. Шаблон четвертого аргумента в случае одного дифференциального уравнения нужно обязательно удалить. Эта запись присвоения Odesolve завершает блок решения уравнения.

Если вы не указали число узлов интегрирования, то оно выбирается системой по умолчанию. В МС14 число узлов по умолчанию равно 1000. Такое число узлов достаточно для достижения разумной точности решения, исключая случаи слишком большого отрезка интегрирования или очень быстро меняющейся функции. Поэтому в МС14 лучше указывать только два аргумента.

В качестве примера возьмем уравнение и начальные условия из задачи, рассмотренной ранее:

, .

Решение ищется на отрезке [0; 3]. На экране набираем

given

y(0) = 2

y:= Оdesolve(x, 3)

Теперь мы получили функцию y(x), которая является приближенным решением. Мы можем получить ее значение в любой точке отрезка [0; 3]. Для контроля возьмем ее значение в точке 1.6: y(1.6) = 3.54039. Воспользуемся результатом, полученным для этой же задачи ранее, в матрице Y в первом столбце найдем значение 1.6 (8 строка), а во втором столбце соответствующее значение y. Это значение оказывается равным 3.54044, что до третьего знака совпадает со значением, полученным функцией Оdesolve. Преимущество функции перед матрицей заключается в том, что мы можем найти значение функции в любой точке, например в точке :. В матрице такого значения мы не найдем, там придется увеличивать число узлов или делать конечную точку отрезка равной числу.

Еще один пример. Требуется найти решение дифференциального уравнения с начальными условиямиz(1) = 3, z’(1) = 1 на отрезке [1; 4] и построить график этого решения. Набираем

given

= 0

z(1) = 3   z′(1) = 1

z:= Odesolve(t,4)

Замечание. На экране система МС14 в записи уравнения выражениезаключит автоматически в круглые скобки.

Вычислим, например, значение решения в точке t = 3.5: z(3.5) = − 0.76854. График решения приведен на рис. 35.

Заметим, что в записи уравнения вместо можно было бы использоватьz’’ и z’, и что записи Odesolve и odesolve система МС14 не различает. Кроме того, вместо буквы z в операторе присвоения можно было использовать любое другое имя, например, kw, решением тогда служила бы функция kw(t). Значение переменной TOL не влияет на точность результата.