Решение систем нелинейных уравнений

Простейшие системы нелинейных уравнений система МС может решать с помощью символьных преобразований. ВНИМАНИЕ! Знаки = в уравнениях набираются не с клавиатуры, а вызываются с панели булевых функций Boolean. Вот несколько примеров:

,,

.

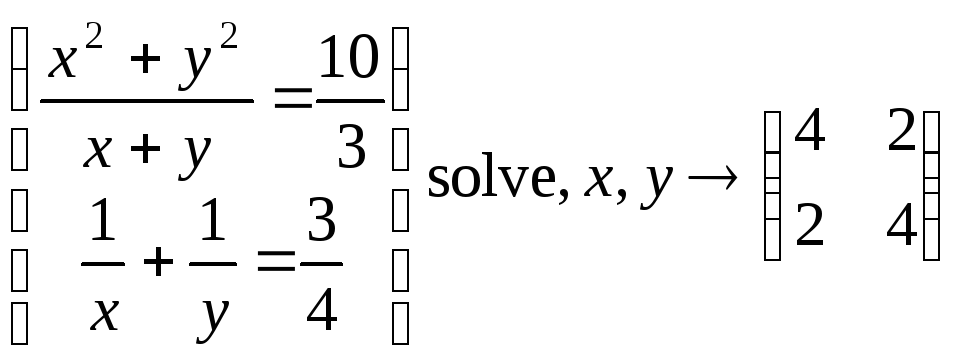Системы, которые не удается решить символьными преобразованиями, можно попытаться решить численными методами. Для этого в системе МС нужно произвести следующие действия:

1. Неизвестным присвоить начальные значения по возможности близкие к ожидаемому решению.

2. В очередном блоке записать с клавиатуры слово given, которое является директивой системы МС и открывает «увеличенный блок», где записываются уравнения системы. В слове given не имеет значения, записано оно прописными буквами или строчными.

3. В последующих блоках записать уравнения, используя знак =, взятый с панели Boolean. В каждом блоке записывается одно уравнение.

4. Записать функцию Find(x,y,z,…), где в скобках указываются неизвестные системы уравнений. Лишние шаблоны в аргументе функции можно удалить. Эта функция, записанная в отдельном блоке, завершает «увеличенный блок», посвященный решению системы. Значения этой функции (решение системы) образуют вектор. Можно какому-нибудь переменному присвоить значение этой функции. Можно просто посмотреть ответы на экране, поставив после функции знак = с клавиатуры.

Рассмотрим пример

given

Итак, система MATHCAD выдала решение x = 1.109, y = 0.613. Произведем проверку

.

Видим, что с точностью до тысячных равенства системы выполнены. Эта точность соответствует точности, с которой выведены на экран результаты. На самом деле результат значительно лучше. Используем найденные значения z, а не их округленную запись на экране:

.

Таким образом, ошибка появляется только в пятнадцатом знаке после запятой!

Очень многое зависит от задания начальных значений. Если в приведенном выше примере изменить начальные условия, задав , то система сообщит, что решение задачи не найдено. Неизвестные и их начальные значения можно задавать в векторном виде. Пример (установите начало нумерации элементов матриц с 1):

given

.

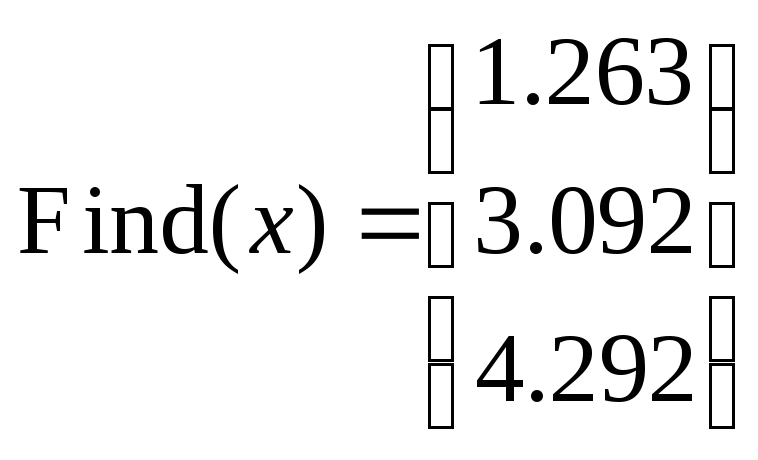Точность решения системы уравнений с помощью функции Find регулируется двумя системными переменными TOL и CTOL, которые можно найти через меню Tools пункт Worksheet Options.

Корни многочлена

Как мы видели на первом занятии, в системе МС имеется возможность разложить многочлен на множители с помощью символьных операций. Но эта возможность реализуется только в том случае, когда получающиеся множители имеют целые коэффициенты. При этом множители не всегда получаются линейными или квадратичными. Проверьте это на многочленах ,,,,. В других случаях для разложения на множители приходится находить корни многочлена. Как это можно сделать в системе МС, описано выше. Следует, однако, учесть, что функцияpolyroots гарантирует хорошие результаты только для многочленов невысокой степени. Аналогичным недостатком обладает и директива solve для символьного нахождения корней. Рассмотрим следующий пример. Пусть

.

Этот многочлен имеет два кратных корня 1.5 и 1.9 кратности 2. Раскроем скобки, для чего воспользуемся директивой Collect из меню Symbolics (из-за формата страницы результат записан в двух строчках):

Попробуем найти корни с помощью символьной операции solve (на экране условие записывается в одной строке):

Как видим, корни найдены точно, и каждый показан столько раз, какова его кратность. Используем функцию polyroots. Для этого потребуется вектор из коэффициентов многочлена. Чтобы его компоненты не набирать вручную, воспользуемся пунктом Polynomial coefficient из меню Symbolics, выделив сначала переменную x в записи многочлена. В результате получим

Тот же результат можно получить кнопкой coeffs на панели Symbolic. Скопируем результат и выполним присвоение:

. Вычислим корни: .

В этом случае результаты значительно отличаются от точных корней. Это связано и со степенью многочлена, которая является довольно высокой, и с наличием кратных корней, которые превратились в комплексно сопряженные простые корни. Если по этим корням получить многочлен, производя округления с точностью до 5 знаков после запятой, то получим многочлен, коэффициенты которого отличаются от исходных только в четвертом знаке.

Посмотрим, как изменение коэффициентов влияет на корни. Для этого в многочлене p(x) уменьшим коэффициент при x на единицу последнего знака, т.е. на ,. Найдем корни с помощью функцииpolyroots. Увидим, что изменения происходят уже в третьем знаке после десятичной точки, причем простой вещественный корень 2 превращается в комплексный:

.

Если воспользоваться символьным нахождением корней, то получим результат, заметно отличающийся от ранее вычисленного. В частности, корень 2 исходного многочлена превращается в корень, приближенно равный 1.8 (из-за громоздких записей распечатка не приводится). Таким образом, мы убедились, что для многочлена высокой степени малое изменение коэффициентов может вызвать существенное изменение корней и к полученным результатам с помощью функции polyroots нужно относиться осторожно.

Если подставить найденные значения корней в многочлен, то для корней, вычисленных символьным методом, результаты будут иметь порядок , а для корней, полученных с помощью функцииpolyroots, – порядок .

Если результат, полученный символьным способом, желательно округлить до меньшего числа цифр после десятичной точки, то нужно его выделить, а затем в меню Symbolics выбрать пункт Evaluate и в развернувшемся меню пункт Floating Point. В появившемся окне указывается общее число значащих цифр результата (до точки и после нее, нули слева не учитываются). То же можно сделать и с помощью панели Symbolic. Округлим корни предыдущего многочлена до пяти цифр после точки, используя эту панель. Из-за громоздкой записи здесь в исходных корнях приведены только 7 цифр после точки, на экране их 19.

.

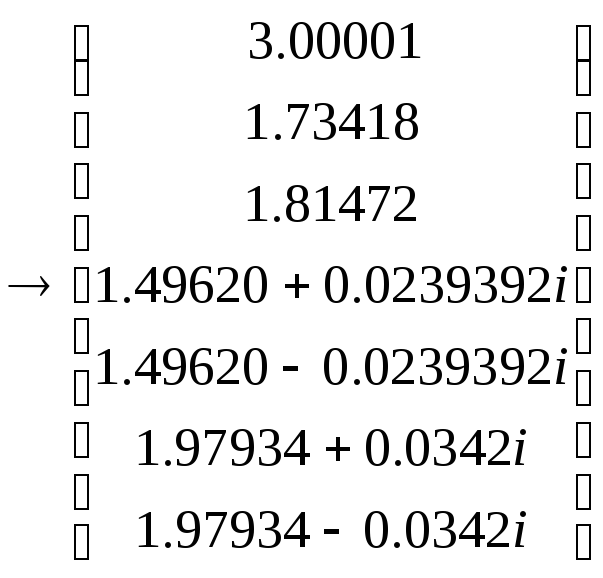После того как найдены корни многочлена, мы можем представить его в виде произведения. Произведение будет содержать в вещественном случае линейные и квадратичные множители, в комплексном случае – только линейные. Произведем это разложение для рассмотренного выше многочлена. Используем корни, округленные до пяти цифр после запятой. Это округление у нас уже имеется. Чтобы не переписывать длинные наборы цифр, скопируем набор корней и создадим соответствующую векторную величину

.

Найдем квадратичные множители. Для этого используем пары комплексно сопряженных корней. Если за счет вычислений комплексные корни отличаются от комплексно сопряженных на величину, лежащую за пределами заданной точности, то их нужно исправить. Исправить нужно так, чтобы они стали комплексно сопряженными. Для удобства преобразований используем кнопку стрелка с шаблоном на панели Symbolic. Сначала набираем выражение . Затем нажимаем стрелку с шаблоном. Нажимаемcollect на той же панели. Клавишей табулирования переходим на следующий шаблон. Нажимаем кнопку float. Вписываем 6 в шаблон. Переходим на следующий шаблон и удаляем его. Щелкаем мышью за пределами блока. В результате получаем

.

Аналогично получим

.

Теперь можно записать разложение многочлена на множители (из-за размера страницы мы приводим только 2 цифры после десятичной точки):

.