Методы решения систем нелинейных уравнений

Систему из n нелинейных уравнений с n неизвестными будем записывать в виде , где

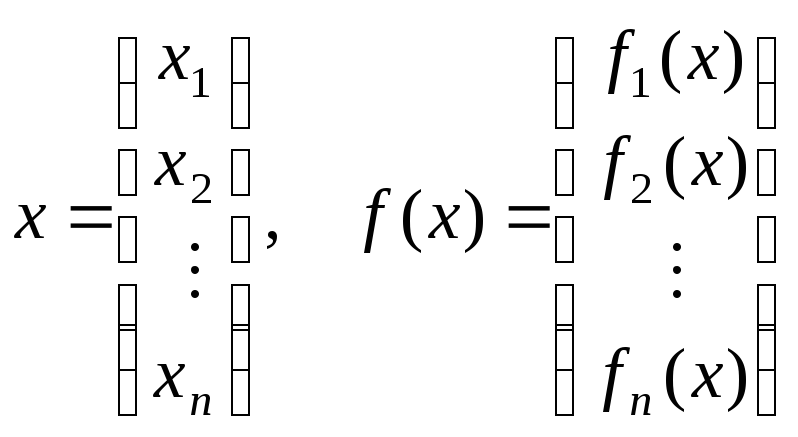–векторы, ,, – функции отn переменных. Мы рассмотрим только два из многочисленных методов, применяемых для решения систем уравнений.

Метод Ньютона для систем уравнений

Обозначим через матрицу Якоби функции, т.е.

.

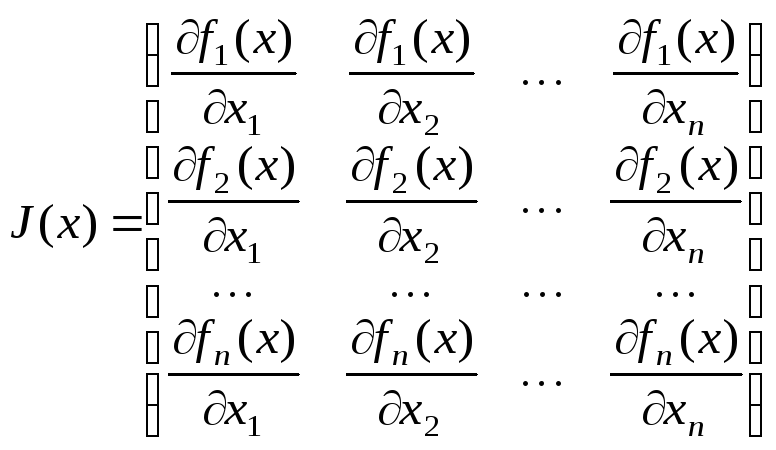Выбирается начальное приближение . Следующие приближения находятся по формуле

, .

Процесс вычислений, как правило, останавливается, если , гдеε – заданная точность. Для гарантии сходимости процесса нужно, чтобы точка находилась вблизи точного решения. При произвольном выборепроцесс может расходиться. Обычно перед применением метода Ньютона находят, используя методы минимизации функции.

Скорость сходимости – квадратичная, как и в случае одного уравнения.

Метод итераций для систем уравнений

Систему преобразуют в равносильную систему уравнений вида . Выбирают начальное приближениеи далее получают следующие приближения,.

Обозначим через матрицу Якоби функции. Есливыбрано достаточно близко к точному решениюи, то процесс будет сходиться. Скорость сходимости метода – линейная, т.е., где– некоторые положительные числа,.

Некоторые сведения о полиномах и их корнях

Полином, иначе многочлен, степени n записывается так: , где– числа,. Константасчитается полиномом нулевой степени.

Основная теорема алгебры утверждает, что любой многочлен ненулевой степени имеет хотя бы один корень. По теореме Безу многочлен всегда делится на двучлен , гдеc – корень. Поэтому любой полином ненулевой степени n можно разложить на множители

,

где – попарно различные корни многочлена (возможно комплексные);– натуральные числа,. Если, тоназывается корнем кратности. Если, тоназывается простым корнем многочлена.

Верно следующее утверждение. Корень c является корнем кратности k тогда и только тогда, когда ,, …,, а.

Определение. Полином делится на полиномс остатком, если, где– полином (частное),– полином, степень которогострого меньше степени делителя . Полиномделится на полином(илиявляется делителем), если, т.е. если остаток равен нулю.

Легко заметить, что если – делитель полинома, то, где– число, отличное от нуля, тоже является делителем многочлена.

Алгоритм деления многочленов следующий. Пусть обозначает степень полинома. Пусть также,,, ,т.е. ,.

Если <, то,и деление закончено, иначе

, (3)

где ,. Последний многочлен запишем в виде.

Если <, то,и деление закончено, иначе повторяем шаг алгоритма для многочлена:

, (4)

где ,. Подставив в (3) выражение (4), получим

.

Если <, то процесс деления закончен, иначе выполняем шаг алгоритма для многочленаи т.д.

В результате получаем, что

. Тогда частное – это , остаток.

Определение. Наибольшим общим делителем полиномов иназывается многочлен наибольшей степени, являющийся делителем этих двух полиномов.

Наибольший общий делитель определяется с точностью до умножения на число, отличное от нуля. Если наибольший общий делитель есть константа, то многочлены называются взаимно простыми.

Очевидно, что корни наибольшего общего делителя многочленов ии только они являются общими корнямии.

Справедлива следующая теорема. Кратные корни многочлена и только они являются корнями наибольшего общего делителя многочлена и его производной.

Определить, имеют ли многочлены общие корни, можно с помощью результанта. Результантом двух многочленов иназывается определитель матрицы порядка, составленной следующим образом. В первыеm строк пишем коэффициенты , причем в каждой следующей строке производим сдвиг на один элемент вправо, незанятые места в строках заполняем нулями. В остальныеn строк вписываем коэффициенты по тому же правилу (в (m + 1)-й строке запись коэффициентов начинается с первой позиции).

Пример. Пусть ,. Тогда результант равен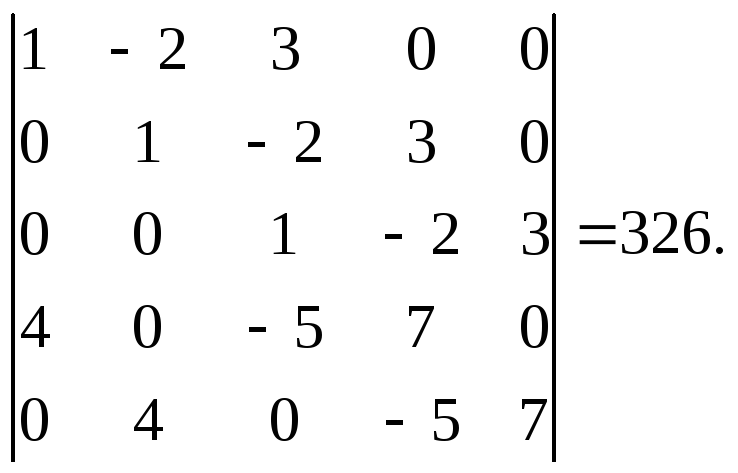

Теорема. Результант равен нулю тогда и только тогда, когда многочлены имеют общие корни.

Лабораторные работы №4 и №5