Метод Гаусса

Метод Гаусса предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Его описание приводится в предположении, что число неизвестных равно числу уравнений и что определитель матрицы коэффициентов системы отличен от нуля (матрица невырожденная).

Пусть задана СЛАУ (запись в матричном виде) Ax = b, где

, ,.

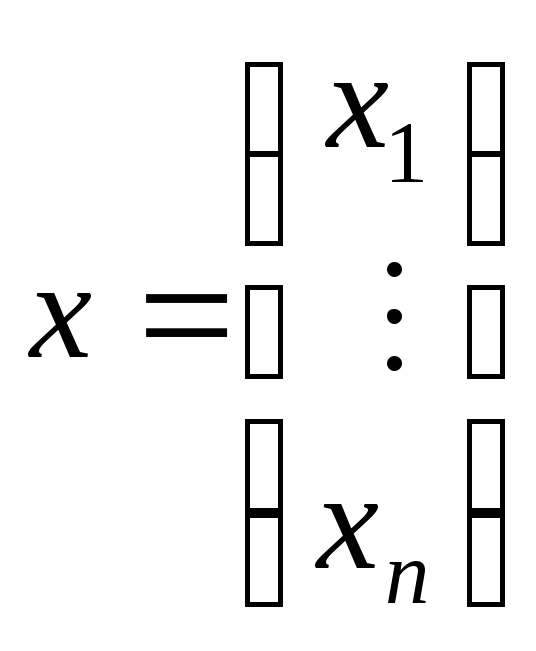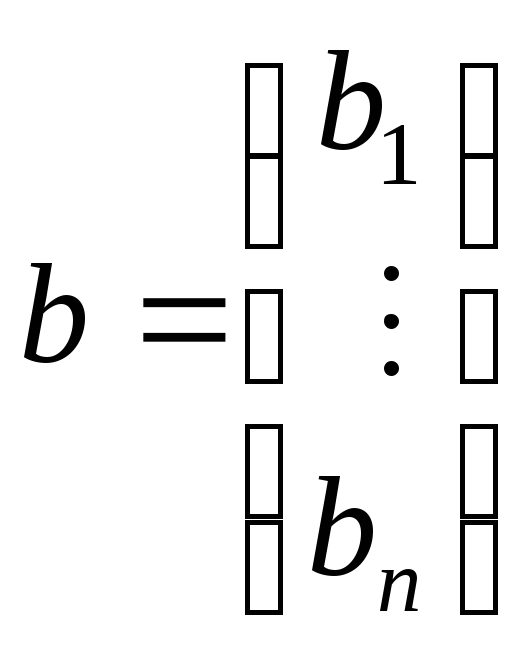Составляется расширенная матрица системы . С элементами этой матрицы выполняются следующие операции, которые обычно называются элементарными:

1. можно менять местами строки;

2. к одной строке можно прибавлять другую, умноженную на любое число;

3. можно умножать строку на любое число, отличное от нуля (используется в основном при вычислениях вручную, на бумаге).

Цель выполнения элементарных операций – получить под главной диагональю матрицы A нули. Этой цели добиваемся последовательными переходами от одной матрицы к другой после выполнения определенного цикла элементарных операций.

От матрицы переходим к матрицеследующим образом. Пусть. Тогда первую строку матрицыоставляем без изменения, т.е.,,. Ко второй строке прибавляем первую строку, умноженную на число, т.е.,,, при этом окажется, что.

К третьей строке прибавляем первую строку, умноженную на число , т.е.,,, при этом окажется, что. Таким же образом преобразуем все строки, т.е. к строке с номеромi прибавляется первая строка, умноженная на число ,,,,. В результате этих вычислений получим матрицу

.

Первый шаг прямого хода метода Гаусса на этом закончен.

Далее переходим к матрице , добиваясь нулей во втором столбце, начиная с третьей строки. Строки 1,2 оставим без изменений. Полагаем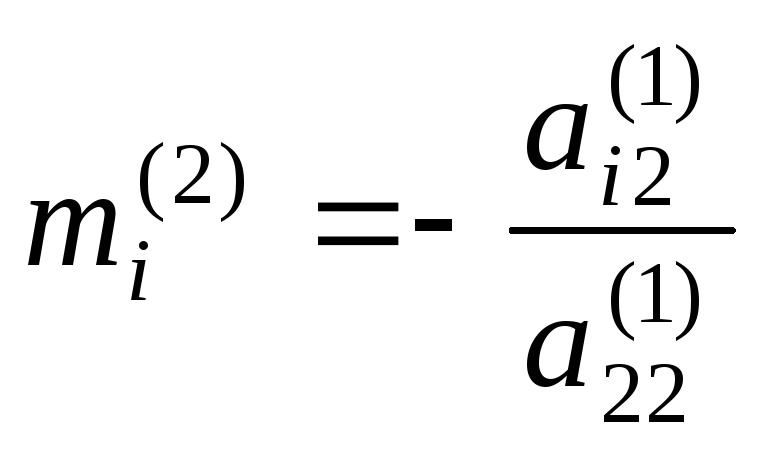,. К строке с номеромматрицыприбавляем вторую строку, умноженную на число,,,,. В действительностиj меняется от 2 до n, так как первый столбец в результате этих действий останется без изменений. Получим матрицу

.

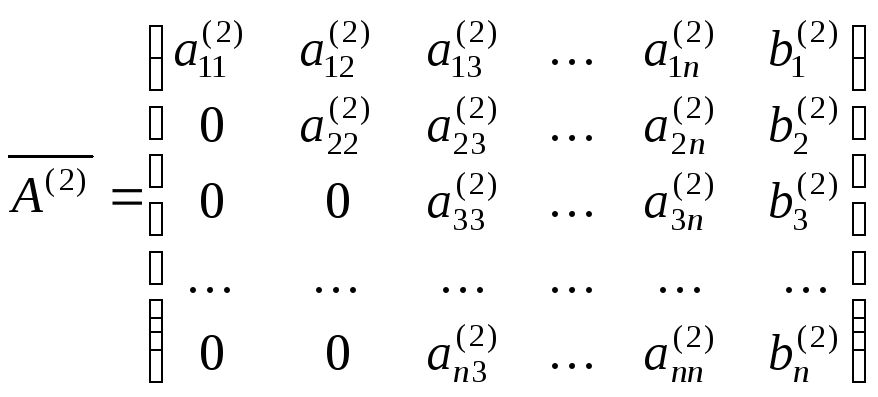На этом закончен второй шаг прямого хода метода Гаусса.

Продолжая вычисления аналогичным образом, переходим к матрице, где в третьем столбце, начиная с четвертой позиции, будут стоять нули. Действуя далее аналогично, придем к матрице

,

у которой под главной диагональю стоят одни нули. Прямой ход метода Гаусса закончен.

Матрице соответствует система уравнений

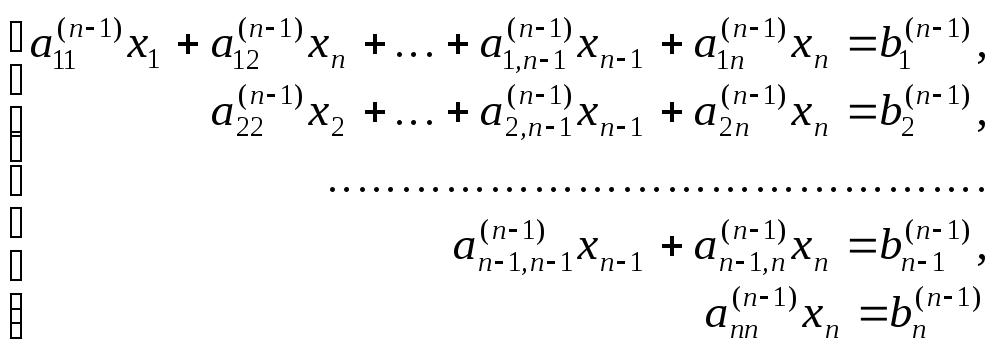
равносильная исходной. Ее решения легко найти по формулам ,(значениеуже найдено) и так далее. Общая формула:

,

Метод Гаусса требует выполнения порядка арифметических операций. Это один из самых экономичных методов.

Метод lu-разложения

Можно показать, что применение метода Гаусса эквивалентно LU-разложению матрицы А, т.е. ее представлению в виде произведения , где

.

Элементы этих матриц находятся по формулам в том порядке, в котором здесь эти формулы выписаны:

,

Такое разложение дает следующий результат:

. Положим , тогда. Получили треугольную систему уравнений

Из этой системы последовательно находим ,. Знаяy, находим x из треугольной системы

Откуда ,.

И в методе Гаусса при решении систем линейных уравнений, и в LU-разложении матрицы приходится выполнять деление на элемент матрицы. Если этот элемент нуль, то процесс остановится, хотя матрица А не вырождена, и решение системы существует. Проблемы возникают и в том случае, когда элемент, на который приходится делить, очень маленький. В этой ситуации предыдущие ошибки, возникающие неизбежно при округлении чисел компьютером, резко увеличиваются и могут стать недопустимо большими. Если действия выполняются на бумаге, то вы просто меняете строки матрицы местами. Аналогично поступают и при программировании метода Гаусса и LU-разложения. При этом обычно выбирают такую строку, где элемент, на который нужно делить, является наибольшим по модулю.

При таком алгоритме при LU-разложении уже получается три матрицы P, L, U. Матрицы L, U – нижняя и верхняя треугольные соответственно, ,,P – матрица перестановок, т.е. квадратная матрица порядка n, в каждой строке и в каждом столбце которой только один элемент равен 1, а все остальные элементы – нули. Эти матрицы связаны соотношением . Такое разложение всегда возможно, если.

Если мы получим такое разложение, то для решения системы обе части умножим слева на матрицуP, , и заменимPA на LU, . Далее действия такие же, как описано выше. ИменноLU-разложение используется в системе MATHCAD для решения систем линейных уравнений.