Число обусловленности матрицы

Решим систему уравнений

(13)

Решать эту систему символьно бессмысленно, так как запись коэффициентов уже предполагает наличие ошибок округления. Создадим матрицу системы и столбец свободных членов: ,. Находим,. Вроде бы получили приемлемый ответ. Изменим на 0.0001 свободный член в третьем уравнении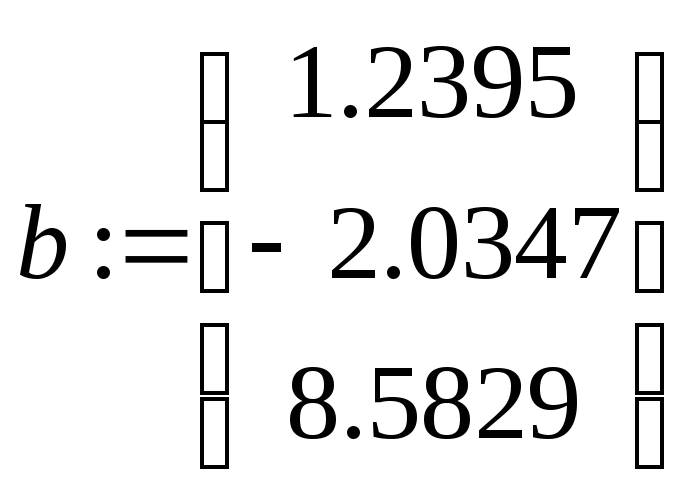. Получим,. Видим, что ответ изменился очень сильно, более чем на 100 по двум компонентам. Так как изменение условий было сделано на границе точности задания коэффициентов, то полученный ранее ответ с точки зрения инженера является неприемлемым. Выясним ранг матрицы:rank(A) = 3. Следовательно, решение системы действительно существует. Найдем число обусловленности матрицы A. Для этой цели имеются три функции, соответствующие трем разным нормам вектора и соответственно трем разным нормам матрицы. Это функции cond1(■), cond2(■), condi(■). Есть еще одна функция обусловленности conde(■), но она с точки зрения математики плохо обоснована, так как соответствует норме матрицы, в которой норма единичной матрицы отлична от 1. Для любопытства вычислим число обусловленности всеми четырьмя способами (на самом деле достаточно одного способа): ,,,. Видим, что в любом варианте число обусловленности матрицыA получилось очень большим, то есть система уравнений является плохо обусловленной.

Из анализа решения системы уравнений (13) получаем вывод, аналогичный выводу, сделанному ранее. Если вы решали систему линейных уравнений с помощью системы MATHCAD (впрочем, и любой другой), то нужно проверить, не является ли система вырожденной или плохо обусловленной, согласуются ли результаты с тем, что ожидалось.

Собственные числа и собственные векторы матрицы

Для нахождения собственных чисел матрицы в МС служит функция eigenvals(■). Эта функция вызывается с помощью кнопки f(x) на панели инструментов, группа функций Vector and Matrix. Результатом действия служит вектор, компонентами которого являются собственные числа. Каждое собственное число встречается столько раз, какова его кратность.

Для нахождения всех собственных векторов используется команда eigenvecs(■). Она вычисляет матрицу, столбцами которой служат собственные векторы, соответствующие собственным числам, полученным командой eigenvals(■). Есть еще одна команда eigenvec(■,■), которая вычисляет только один собственный вектор, соответствующий собственному числу, указанному во втором аргументе.

Рассмотрим пример. Создадим матрицу . Найдем собственные числаи собственные векторы. Таким образом, собственному числу 3 соответствует собственный вектор, равный первому столбцу, а числу − 2 — вектор. Попробуем выполнить эти же действия с помощью символьных операций. В результате получим те же собственные числа, а собственные векторы будут заданы матрицей. Собственные векторы отличаются от полученных ранее. Проверим их соответствие собственным числам:

,

.

Видим, что первый столбец матрицы собственных векторов соответствует второму собственному числу, а второй столбец – первому собственному числу. Если первый столбец матрицы собственных векторов умножить на число, то получим второй столбец из матрицы собственных векторов, вычисленной с помощью знака =. Если второй столбец умножить на число, то получим первый столбец из матрицы собственных векторов, вычисленной с помощью знака =. Такое расхождение в соответствии собственных чисел и собственных векторов при использовании вычислительных и символьных методов наблюдается только в МС14. В более ранних версиях МС при символьных вычислениях порядок собственных векторов соответствует порядку собственных чисел.