Метод наискорейшего спуска

Этот метод требует вычисления частных производных первого порядка от исходной функции. Другое название метода – метод антиградиентного спуска.

Выбирается начальное приближение . В этой точке вычисляется вектор градиента функции

.

По смыслу градиента функция быстрее всего убывает в направлении, противоположном градиенту, т.е. в направлении вектора. Функцияограничивается на прямую,

проходящую через точку и параллельную градиенту

.

Находится точка минимума этой функции ,. Вычисляется новое приближение:,.

После этого процесс повторяется из точки . Получается новое приближениеи т.д.

Вычисления обычно останавливают, если или если.

Метод наискорейшего спуска сходится медленно в случае так называемых овражных функций. График такой функции двух переменных представлен на рис. 5. Линии уровня овражной функции изображены на рис. 6, более темным линиям соответствуют меньшие значения функции.

Следует заметить, что рис. 5, 6 лишь схематически соответствуют овражным функциям. На самом деле «края оврага» должны подниматься значительно круче, а овалы соответствующих замкнутых линий уровня должны сжаться практически в куски линий. На рисунках это выглядит мало понятно.

Метод Ньютона

Этот метод использует производные первого и второго порядка. Метод заключается в следующем. Выбирается начальная точка . Каждое следующее приближение подсчитывается по формуле, где

, .

Процесс останавливается, если или.

Метод Ньютона сходится очень быстро, если начальное приближение достаточно близко к точке минимума. Во многих случаях метод может расходиться, если начальное приближение взято неудачно, т.е. далеко от точки минимума. Поэтому обычно в начале процесса применяются другие методы, чтобы подойти к точке минимума поближе, а на заключительном этапе применяется метод Ньютона.

Преобразования Фурье и Лапласа

Для анализа колебательных процессов используют ряды Фурье. Как правило, используется комплексная форма ряда Фурье.

При наличии некоторых ограничений функцию , заданную на отрезке [0; T ], можно записать в виде , где. Для приближенного вычисления коэффициентовприменим формулу прямоугольников. Отрезок [0; T ] разобьем на N частей точками ,,…,и обозначим. Тогда

и соответственно

. (9)

Здесь мы видим, что коэффициент , вычисляемый приближенно, т.е., не зависит от длины отрезка [0;T ], а зависит только от числа узлов N и значений функции в этих узлах.

Покажем, что

(10)

при любом целом k. Действительно

.

Так как для любого целогоm, то .

В силу этого свойства коэффициентов имеет смысл вычислять эти коэффициенты лишь приN последовательных значениях индекса q.

Составим функцию . Несложно показать, что на узлахвыполняется равенство, т.е. в наших обозначениях. Однако вне узлов на [0;T ] расхождение значений может быть весьма большим даже при больших N. Например, возьмем функцию . Подсчет показывает, что для нее,,при.

Таким образом,

.

Возьмем . Получим

.

Если число N большое, то . В итоге получили, что расхождение равно приближенно.

Такого большого расхождения функций вне узлов решетки можно избежать. В силу (10) , т.е. коэффициентыможно брать и с отрицательными индексами. Положим

.

Для этой функции при любом выполняется условие, если.

Равенство называется тригонометрической интерполяцией функцииf(x), коэффициенты называются дискретными коэффициентами Фурье.

Так как , то соответствие между векторамии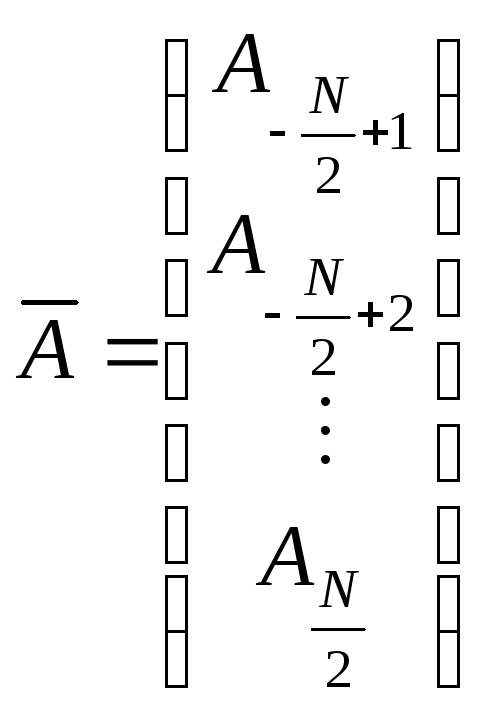является взаимно однозначным. Здесь мы предположили, чтоN – четное число.

Преобразование называется дискретным преобразованием Фурье, а преобразование– обратным дискретным преобразованием Фурье.

Из общего курса математики известно, что для функций, заданных на всей оси, при некоторых ограничениях определено преобразование Фурье в комплексной форме , где, и обратное преобразование Фурье,. Это так называемая симметричная форма преобразований Фурье. Кроме этих формул используются и другие формулы, отличающиеся от них коэффициентами перед интегралами и знаками в показателе экспоненты. Это объясняется тем, что инженеров обычно интересует, как величина амплитудызависит от частоты, а само значение этой амплитуды является несущественным. Функцияназывается спектральной плотностью или спектральной функцией функции.

В системе MATHCAD 14 при символьных преобразованиях используются несимметричные формулы преобразований Фурье:

(11)

(12)

В более ранних версиях системы знаки показателей экспоненты – противоположные. Следует помнить, что преобразование Фурье применяется только к абсолютно интегрируемым функциям, т.е. к функциям, для которых сходится несобственный интеграл. Последнее не означает, что этот интеграл можно вычислить, используя таблицу интегралов. (Если интеграл расходится, то результатом преобразования Фурье может оказаться обобщенная функция. Этот математический объект в некотором отношении похож на функцию, но в действительности функцией не является.) Если говорить грубо, то сходимость интегралаозначает, чтопри, причем довольно быстро, быстрее, чем. Функций, которые записываются с помощью элементарных функций и удовлетворяют поставленным условиям, сравнительно мало.

Дискретное преобразование Фурье является некоторым приближением преобразования Фурье. Понимать это нужно так. Пусть преобразование Фурье применяется к функции и дает спектральную функцию. Выделим отрезок [a; b], вне которого функция мала и на котором отражены наиболее важные черты графика. Длину этого отрезка обозначим черезT. Разобьем отрезок на N частей (N – большое число) и найдем дискретное преобразование Фурье с периодом T. Если в преобразовании Фурье использовалась формула (11), то . Равенство будет тем точнее, чем больше величиныT и N.

Преобразование Лапласа достаточно подробно рассматривалось в общем курсе математики. Так как вMATHCAD это преобразование выполняется только в символьном виде, то здесь мы на этом преобразовании останавливаться не будем.