
- •Введение
- •Раздел 1
- •§ 2. Контрольные вопросы и задания
- •§ 3. Примеры решения задач
- •§ 4. Задачи и упражнения для самостоятельной работы
- •Раздел 2 линейные операторы в евклидовых и унитарных пространствах
- •§ 1. Основные понятия и теоремы
- •§ 2. Контрольные вопросы и задания
- •§ 3. Примеры решения задач
- •Этой формулой и выражается искомая связь между АиА*. Если базис ортонормированный, то матрица гединичная матрица и тогда.
- •§ 4. Задачи и упражнения для самостоятельной работы
- •Литература
§ 2. Контрольные вопросы и задания
Пусть А – оператор поворота векторов на угол в евклидовом пространстве V2 (повороты векторов на плоскости). Какой оператор является сопряженным к нему
Верно ли утверждение о том, что число 1 + i является собственным значением некоторого линейного оператора, который имеет симметричную матрицу
Являются ли ортогональными нуль-оператор, тождественный оператор и оператор подобия с коэффициентом подобия
Известно, что линейный оператор А переводит ортонормированный базис {ei}
 в другой ортонормированный базис {fi}
в другой ортонормированный базис {fi} . Следует ли отсюда, что А
– ортогональный
оператор
. Следует ли отсюда, что А
– ортогональный
операторМожет ли собственное значение ортогонального оператора принимать значение 2, 0, 1, –1.
Для любого ли линейного оператора, действующего в унитарном пространстве, существует сопряженный оператор Линеен ли он
Как связаны между собой матрицы линейных операторов А и А*, заданных в одном и том же ортонормированном базисе
Как связаны между собой собственные значения линейных операторов А и А*, действующих в унитарном пространстве
Являются ли эрмитовыми нуль-оператор, тождественный оператор, оператор подобия с вещественным коэффициентом подобия и оператор подобия с комплексным коэффициентом подобия
Верно ли утверждение о том, что если матрица оператора эрмитова в некотором ортонормированном базисе, то она эрмитова и в любом другом ортонормированном базисе
Может ли для какого-нибудь элемента x быть верным равенство (Ax, x) = 1 + i , где А эрмитов оператор
Может ли число 1 + i быть собственным значением некоторого эрмитового оператора
§ 3. Примеры решения задач
1. Пусть А – матрица линейного оператора в базисе {ei} евклидового пространства, А* – матрица сопряженного оператора в том же базисе, а Г – матрица Грамма базиса {ei}. Найти связь А и А* в случае унитарного пространства. Как связаны А и А* в ортонормированном базисе?
Решение.
Если
![]()
базис унитарного пространства, то
базис унитарного пространства, то
![]() и, обозначая через
и, обозначая через![]() элементы матрицы линейного оператораА,
а через
элементы матрицы линейного оператораА,
а через
![]() элементы матрицы оператораА*,
сопряженного к оператору А,
получим:
элементы матрицы оператораА*,
сопряженного к оператору А,
получим:
![]()

 .
.
Из определения А* следует:
![]()



![]()
 ,
,
где
![]()
элементы матрицы Грамма.
элементы матрицы Грамма.
Из этого равенства делаем заключение
![]()
![]()
![]()
![]()
![]() .
.
Этой формулой и выражается искомая связь между АиА*. Если базис ортонормированный, то матрица гединичная матрица и тогда.
а)
![]() в унитарном пространстве,
б) А*
=
в унитарном пространстве,
б) А*
=
![]() Т
в
ортонормированном базисе. ▲
Т
в
ортонормированном базисе. ▲
2. Оператор А задан матрицей в базисе с матрицей Грамма Г. Будет ли оператор А эрмитовым:
 ?
?
Решение.
Воспользуемся
формулой, полученной в задаче 1˚
![]() .
Определитель матрицы Грамма равен
единице, поэтому матрица, обратная к
матрице Грамма, есть транспонированная
матрица из алгебраических дополнений
к элементам матрицы Грамма
.
Определитель матрицы Грамма равен
единице, поэтому матрица, обратная к
матрице Грамма, есть транспонированная
матрица из алгебраических дополнений
к элементам матрицы Грамма
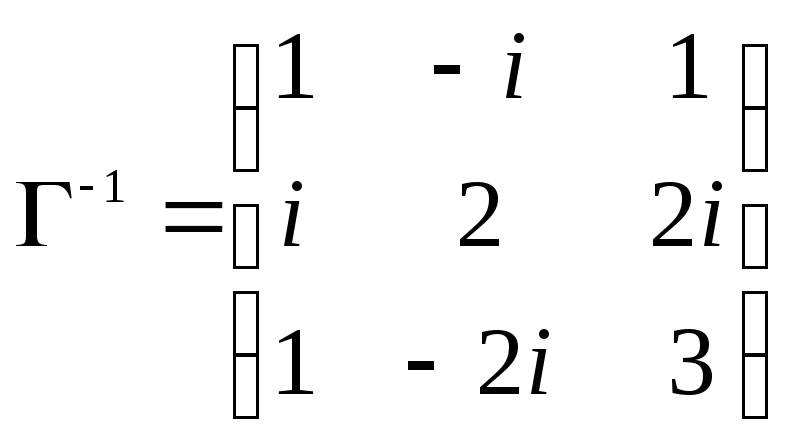 . Тогда
. Тогда
 =
=
= =
= =
= .
.
Оператор А совпадает с оператором А*, следовательно оператор А эрмитов.
да. ▲
3. Задана матрица линейного оператора А в евклидовом пространстве в некотором базисе и Г – матрица Грамма этого базиса. Найти А*:
 .
.
Решение.
Воспользуемся
формулой, полученной в задаче 1
![]() .
В евклидовом пространстве в этой формуле
отсутствует знак комплексного сопряжения
.
В евклидовом пространстве в этой формуле
отсутствует знак комплексного сопряжения
![]() .
Определитель матрицы Грамма равен
единице, поэтому матрица, обратная к
матрице Грамма, есть транспонированная
матрица из алгебраических дополнений
к элементам матрицы Грамма
.
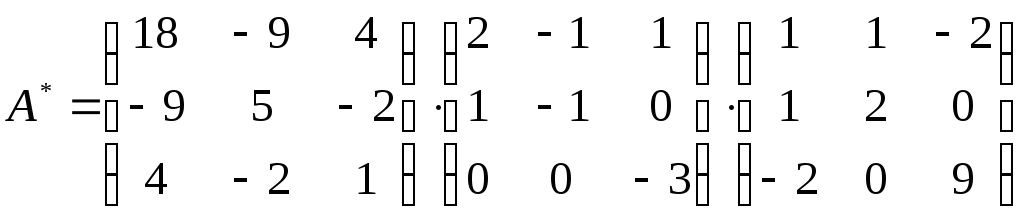
Определитель матрицы Грамма равен
единице, поэтому матрица, обратная к
матрице Грамма, есть транспонированная
матрица из алгебраических дополнений
к элементам матрицы Грамма
 . Тогда
. Тогда
 =
=
=
 =
= .
.
 .
▲
.
▲
4.
Пусть {e1,
e2}
– ортонормированный базис в унитарном
пространстве Еn.
Матрица линейного оператора А,
заданного в базисе {f1,
f2}
пространства Еn,
имеет вид:
![]() .
НайтиА*
в базисе {fi},
если f1
= е1+
е2,
f2
= – е1
– iе2.
.
НайтиА*
в базисе {fi},
если f1
= е1+
е2,
f2
= – е1
– iе2.
Решение. Составим матрицу Грамма для системы векторов f1 = е1 + е2,
f2 = – е1 – iе2 и найдем к ней обратную
 =
=
![]() .
.![]() .
.
Теперь
воспользуемся формулой
![]() .
.
![]() =
=![]() =
=
=
![]() =
=![]() =
=![]() .
.
![]() .
▲
.
▲
5.
Линейный оператор А
в некотором базисе задан своей матрицей.
Скалярное произведение (х,
у)
задано в том же базисе. Найти матрицу
А*,
если:
 ;
(х,
у)
= 2х1у1
– х1у2
– х2у1
+ 2х2у2
– х2у3
– х3у2
+ х3у3.
;
(х,
у)
= 2х1у1
– х1у2
– х2у1
+ 2х2у2
– х2у3
– х3у2
+ х3у3.
Решение.
По
заданному
скалярному
произведению (х,
у)
составим матрицу Грамма, учитывая, что
ее элементы
![]() совпадают
с коэффициентами
при хiуj
, а также
найдем обратную к ней матрицу.
совпадают
с коэффициентами
при хiуj
, а также
найдем обратную к ней матрицу.
 и
и
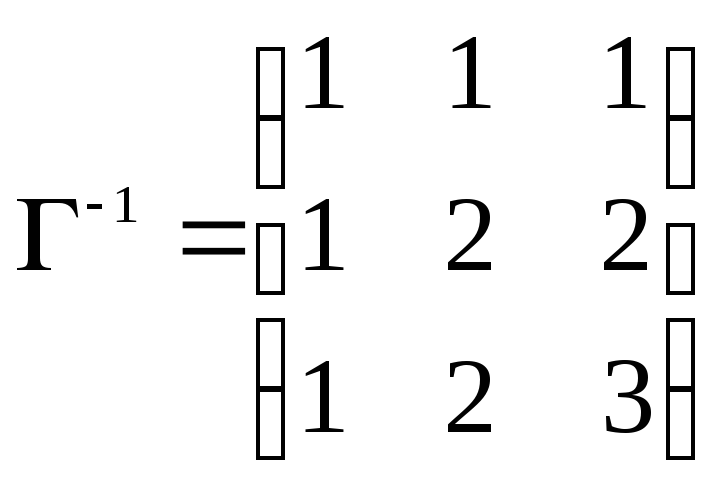 .
Тогда
.
Тогда
![]() =
=
![]() =
= =
=
=
 =
= .
.
 .
▲
.
▲
6.
Линейный оператор А
евклидового
пространства задан в базисе {f1,
f2,
f3
} матрицей А;
{e1,
e2,
e3}
– ортонормированный базис. Является
ли оператор А
ортогональным, если: f1
= е1,
f2
= –е1
+ е2,
f3
= е1
– е2
+ е3
;
 .
.
Решение. Записывая координаты векторов f1, f2, f3 в базисе {e1, e2, e3} в столбцы матрицы Р, получим матрицу перехода из базиса {e1, e2, e3} в базис {f1, f2, f3 }.
 .
.
Найдем матрицу оператора А в ортонормированном базисе. Это удобно, потому что в таком матрица ортогонального оператора должна быть ортогональной и, следовательно, удовлетворять условию ААТ = Е.
![]() =
= =
=
= =
= .
.
Для
матрицы (и оператора)
![]() не выполнено условиеААТ
= Е.
Оператор А
не ортогональный.
не выполнено условиеААТ
= Е.
Оператор А
не ортогональный.
нет. ▲
7. Линейный оператор А переводит векторы а1, а2 в векторы b1, b2, которые заданы своими координатами в некотором ортонормированном базисе. Является ли оператор А ортогональным, если а1(3, 4), а2(1, 3), b1(5, 0), b2(3, 1)?
Решение.
Записывая
координаты векторов а1(3,
4), а2(1,
3), а также векторов b1(5,
0), b2(3,
1) в столбцы матриц, получим матрицы
![]() и
и![]() такие, что
такие, что![]()
![]() .
.
![]() =
=
![]() =
=![]() .
.
В ортонормированном базисе матрица ортогонального оператора должна удовлетворять условию ААТ = Е, т. е. столбцы и строки матрицы должны образовывать ортонормированные системы векторов. Для полученной матрицы оператора А это условие выполнено. Оператор А ортогонален.
да. ▲
8. Является ли унитарным оператор А, действующий на векторы ортонормированного базиса по формулам:
Ае1=![]() (е1
– ie2),
Ae2
=
(е1
– ie2),
Ae2
=![]() (2ie1+е2
– 2iе3),
Ae3
=
(2ie1+е2
– 2iе3),
Ae3
=
![]() (e1–2iе2
+ 2е3).
(e1–2iе2
+ 2е3).
Решение. Построим матрицу оператора А, записывая координаты векторов Ае1, Ае2, Ае3 в столбцы матрицы
 .
Тогда
.
Тогда
 .
.
В ортонормированном базисе матрица оператора А* может быть получена из матрицы оператора А, если матрицу А транспонировать и к ее элементам взять комплексно сопряженные. Именно так мы и поступили.
Условие
унитарности оператора (и матрицы) имеет
такой вид
![]() .
.
![]() =
= .
.
Для этой матрицы не выполнено условие унитарности. Оператор не унитарен. нет. ▲
9.
Линейный оператор А
в унитарном пространстве со стандартным
скалярным произведением переводит
столбцы матрицы М1
в столбцы матрицы М2.
Является ли оператор унитарным, если
 ,
, ?
?
Решение. По условию задачи АМ1 = М2 т. е.
А
=
![]() =
=![]()

 =
=
=

 =
= .
.
Найдена
матрица оператора А в ортонормированном
базисе. Условие унитарности оператора
(и его матрицы в ортонормированном
базисе) имеет вид
![]() и в данном случае оно не выполнено.
Оператор не унитарен.
нет.
▲
и в данном случае оно не выполнено.
Оператор не унитарен.
нет.
▲
10.Найти собственные значения и какую-либо
максимальную ортонормированную систему
собственных векторов ортогонального
оператора, заданного в некотором
ортонормированном базисе евклидового
пространства матрицей: .
.
Решение. Для нахождения собственных значений оператора составим и решим характеристическое уравнение:
![]() =
=
 =
=![]() = 0.
= 0.
Чтобы
найти собственные (их может быть
несколько, т. к. собственное значение
![]() кратное) векторы, соответствующие
собственному значению
кратное) векторы, соответствующие
собственному значению![]() .
Составим систему уравнений
.
Составим систему уравнений![]() и решим ее. Решения системы как раз и
являются собственными векторами.
и решим ее. Решения системы как раз и
являются собственными векторами.
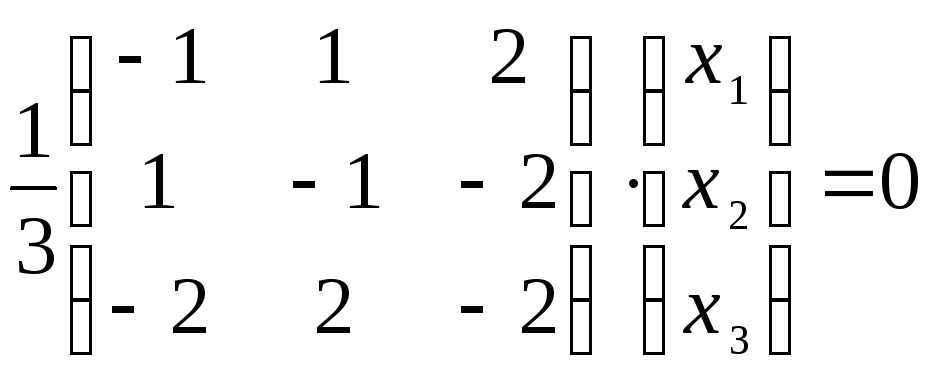

 .
.
Множество решений этой системы образует
линейное пространство размерности 1
(![]() ).
Базис этого пространства образует,
например, вектор (1, 1, 0). Нормируя его,
получаем максимальную ортонормированную
систему собственных векторов линейного
оператора, состоящую из одного вектора
).
Базис этого пространства образует,
например, вектор (1, 1, 0). Нормируя его,
получаем максимальную ортонормированную
систему собственных векторов линейного
оператора, состоящую из одного вектора![]() ,
отвечающего собственному значению
,
отвечающего собственному значению![]() . з)1= 1,f2=
. з)1= 1,f2=![]() (1,
1, 0). ▲
(1,
1, 0). ▲
11.Найти нормальную жорданову форму
матрицы линейного оператораА= и базис, в котором матрица оператора
имеет жорданову форму.
и базис, в котором матрица оператора
имеет жорданову форму.
Решение.
Для матрицы линейного оператора А
=
 составим и решим характеристическое
уравнение: det(A
E)
= 0 .
составим и решим характеристическое
уравнение: det(A
E)
= 0 .
Получим:
 =
=
![]() .
.
Тогда:
![]() = 0 и, следовательно,1,
2 = –1; 3,
4 = 1.
= 0 и, следовательно,1,
2 = –1; 3,
4 = 1.
a)
Рассмотрим оператор А-1
= АE
= А+E
=
 .
Ищем собственные векторы оператораА
при
=
1, т. е. ядро оператора А-1.
Для этого решим систему четырех линейных
однородных уравнений с матрицей А-1.
Из третьего и четвертого уравнений
системы видно, что
.
Ищем собственные векторы оператораА
при
=
1, т. е. ядро оператора А-1.
Для этого решим систему четырех линейных
однородных уравнений с матрицей А-1.
Из третьего и четвертого уравнений
системы видно, что
![]() .
Тогда можно легко установить, что
.
Тогда можно легко установить, что![]() .
Векторf1
(1, 1, 0, 0)
единственный собственный вектор
оператора А,
соответствующий собственному значению
= 1
и образует базис ядра оператора А–1.
Далее ищем базис образа оператора А–1:
.
Векторf1
(1, 1, 0, 0)
единственный собственный вектор
оператора А,
соответствующий собственному значению
= 1
и образует базис ядра оператора А–1.
Далее ищем базис образа оператора А–1:
 .
.
Отметив, что для векторов f2, f3, f4 существует соотношение: f3 + f4 – f2 = (0, 0, 0, 1), находим базис образа оператора А–1:
{1 (1, 1, 0, 0), 2 (0, –1, 1, 1), 3 (0, 0, 0, 1).
Отметив,
что векторы f1
и
![]() совпадают, делаем вывод о том, что этот
вектор образует базис пересечения
образа и ядра оператора А-1.
совпадают, делаем вывод о том, что этот
вектор образует базис пересечения
образа и ядра оператора А-1.
Кратность
корня λ = 1
равна двум, а собственный вектор,
соответствующий этому собственному
значению, только один. Поэтому, полагаем
g1
равным
вектору
![]() ,
а еще один вектор жорданового базиса
ищем, как прообраз первого слоя для
,
а еще один вектор жорданового базиса
ищем, как прообраз первого слоя для![]() .
Решаем неоднородную систему линейных
уравнений
.
Решаем неоднородную систему линейных
уравнений![]() и находим второй векторg2(1,
3/4, 0, 0)
жорданового
базиса, соответствующего собственному
значению
= 1
кратности два. При этом, что характерно,
у вектора
и находим второй векторg2(1,
3/4, 0, 0)
жорданового
базиса, соответствующего собственному
значению
= 1
кратности два. При этом, что характерно,
у вектора
![]() нет прообраза второго слоя, ибо система
нет прообраза второго слоя, ибо система![]() с расширенной матрицей
с расширенной матрицей

решений не имеет. Это и не случайно, потому что собственному значению = 1 кратности 2 должно соответствует два вектора жорданового базиса оператора А:
g1(1, 1, 0, 0); g2(1, 3/4, 0, 0).
При этом отметим, что:
![]() .
.
б) Теперь рассмотрим собственное значение = 1 и, соответственно, оператор А1=А+Е:
 .
.
Найдем ядро этого оператора, т.е. собственные векторы оператора А при λ = 1.
 .
.
Вектор f1 (1, 1, 1, 1) образует базис ядра оператора А1 и является единственным собственным вектором оператора А, отвечающим собственному значению = 1 .
Ищем базис образа М(А1) оператора А1 .
 .
.
Отмечая, что f1 = f2 + f3 + f4, заключаем: базисом пересечения ядра и образа оператора A1 является вектор f1.
Так как собственный вектор только один, а собственное значение имеет кратность 2, требуется найти еще один вектор жорданового базиса. Поэтому полагаем g3 равным вектору1(1, 1, 1, 1), а еще один вектор жорданового базиса ищем как прообраз первого слоя для1(1, 1, 1, 1). Для этого решаем неоднородную систему линейных уравненийA1g4=1и находим векторg4(0, 1/2, 0, 1/2) жорданового базиса, соответствующего собственному значению= 1 кратности два. При этом у вектора1(1, 1, 1, 1) нет прообраза второго слоя, ибо системаA1y=g4с расширенной матрицей

решений не имеет. И вновь это не случайно, потому что собственному значению = 1 кратности 2 должно соответствовать два вектора жорданового базиса, а они уже найдены:
g3(1, 1, 1, 1); g4(0, 1/2, 0, 1/2).
При
этом отметим, что: Ag3
= g1,
Ag4
= g3
+ g4.
Для
оператора А
найден жорданов базис:
 .
При этом
.
При этом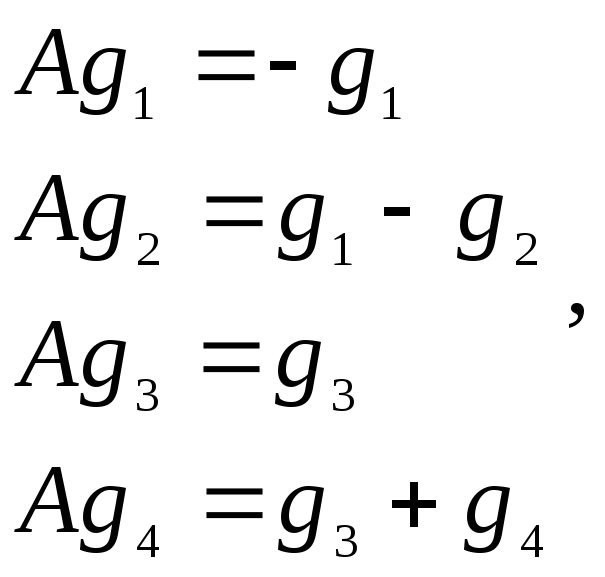 АG
=
АG
=
 .
.

 .▲
.▲
