Раздел 2 линейные операторы в евклидовых и унитарных пространствах

§ 1. Основные понятия и теоремы

Обозначение: L(V,V) – множество линейных операторов, действующих изVвV.

Def. Оператор А*L(V, V) называется оператором, сопряженным к оператору АL(V, V), если х, уV (Ах, у) = (х, А*у).

Любой линейный оператор имеет единственный сопряженный оператор, который также линеен, и при этом:

1. Е* = Е; 2. (А + В)* = А* + В*;

3. (А*) = А* (В евклидовом пространстве (А)* = А*);

4. (А*)* = А; 5. (АВ)* = В*А*; 6. (А^-1)* = (А*)^-1.

Если А – матрица линейного оператора в базисе {e_i} унитарного пространства, а Г – матрица Грамма системы векторов {e_i}, то матрица сопряженного оператора А* в том же базисе может быть найдена по формуле .

Def. Оператор АL(V, V), где V – унитарное пространство, называется эрмитовым (в евклидовом пространстве – самосопряженным), если А* = А.

Def. Операторы А и В называются коммутирующими, если АВ = ВА.

Выражение А, В = АВ – ВА называется коммутатором двух операторов.

Def. Нормой линейного оператора АL(V, V) в нормированном пространстве называется число .

Свойства эрмитовых операторов.

1. Если А – эрмитов оператор, то хV (Ах, х)R.

2.Собственные числа эрмитового оператора А вещественны. При этом собственные векторы, отвечающие различным собственным значениям, ортогональны.

3. Для эрмитового оператора А: .

4. Чтобы АL(V, V) был эрмитов, необходимо и достаточно, чтобы хV Im(Ах, х) = 0.

5. Если А – эрмитов оператор и  – его собственное значение, то хV, ║х║ = 1 |  = (Ах, х).

6. Для эрмитового оператора А его собственные значения  удовлетворяют таким соотношениям: , причем оба равенства достигаются для и.

7. Если А – эрмитов и хV (Ах, х)  0, то .

8. (Теорема о собственном базисе эрмитового оператора). Если АL(V, V) – эрмитов, то в V существует ортонормированный базис, состоящий из собственных векторов оператора А. В этом базисе матрица оператора А имеет диагональный вид, причем по диагонали стоят собственные значения оператора А с учетом их кратности.

9. Произведение двух эрмитовых операторов будет эрмитовым оператором тогда и только тогда, когда операторы коммутируют

(т. е. А, В =0).

Def. Эрмитов оператор называется положительным (А  0), если хV (Ах, х)  0. Если, кроме того, из (Ах, х) = 0  х = , то оператор А называется положительно определенным (А > 0).

10. Собственные значения положительного (положительно определенного) эрмитового оператора неотрицательны (положительны).

Def. Корнем m^й степени ( m – натуральное число) из оператора А называется оператор В такой, что B^m = A.

11. Если А – положительный эрмитов оператор (А  0), то m существует положительный эрмитов оператор . При этом в собственном ортонормированном базисе оператораА матрица оператора В имеет диагональный вид и на диагонали стоят , где_k – собственные значения оператора А.

Def. Если АL(V, V) и х, уV (Ах, Ау) = (х, у), то оператор А называется: а) в унитарном пространстве – унитарным; б) в евклидовом пространстве – ортогональным.

Т. Для того чтобы оператор АL(V, V) был унитарным (ортогональным), необходимо и достаточно, чтобы А* = А^–1 (АА* = Е).

Def. Оператор АL(V, V) называется нормальным, если А*А = АА*.

Примечание: любой унитарный и ортогональный операторы являются нормальными.

Т. Если А – нормальный оператор, то для А и А* в пространстве V существует ортонормированный базис, состоящий из общих собственных векторов операторов А и А*.

Т. Для нормального оператора А существует ортогональный базис, в котором оператор имеет диагональную матрицу, и наоборот, если АL(V, V) имеет ортогональный базис из собственных векторов, то он нормален.

Т. Ортогональный и унитарный операторы имеют полную ортонормированную систему собственных векторов.

Def. Матрица А, у которой a_ijC, называется унитарной, если А*А=АА*=Е. Матрица А, у которой a_ijR, называется ортогональной, если А^ТА=АА^Т=Е.

Т. В ортонормированном базисе матрица унитарного оператора – унитарна, а матрица ортогонального оператора – ортогональна. В базисе, который не является ортонормированным, это, вообще говоря, не верно.

Канонический вид линейного оператора. (Нормальная жорданова форма). К сожалению, не всякий линейный оператор диагонализуем. Но…

Def. Жордановой клеткой G_k() называется квадратная матрица k^го порядка: .

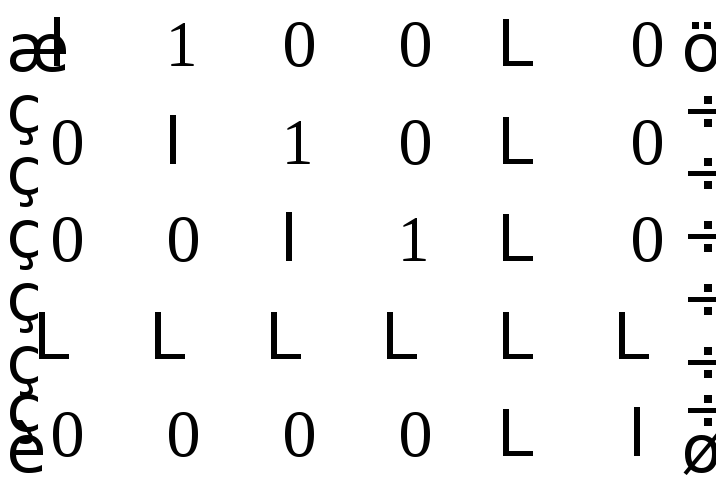Def. Жордановой матрицей называется матрица вида: 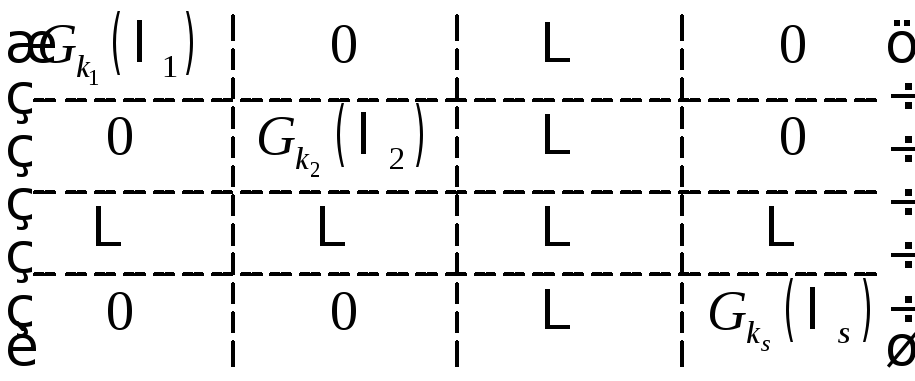, где– жордановы клетки.

Т. Произвольный линейный оператор А в комплексном векторном пространстве имеет базис , в котором матрица оператораА имеет жорданову форму.

Схема построения жорданового базиса:

1. Нахождение собственных векторов и собственных значений оператора А. Если количество собственных линейно независимых векторов равно размерности пространства, то в указанном базисе матрица оператора имеет диагональный вид;

2. Если для кратного собственного значения кратности kколичество линейно независимых собственных векторов также равноk, то в этом базисе матрица также имеет диагональный вид;

3. Для кратных собственных значений таких, что количество линейно независимых собственных векторов меньше кратности корня, поиск базисных векторов производится так:

а) находим собственные векторы А, т. е. базисN(A_) ядра оператораА_=А–Е;

б) находим М(А_) – образ оператораА_и его базис;

в) ищем базис М(А_) ∩N(А_) ;

г) для каждого вектора М(А_) ∩N(А_) находим прообраз 1-го слоятакой, чтоА_, прообраз 2-го слоятакой, чтоА_, и т.д. до тех пор, пока они есть.

Жорданов базис формируется следующим образом:

а) первыми в базис попадают векторы М(А_) ∩ N(А_) вместе со своими прообразами х₁, y₁₁, y₁₂, …, х₂, y₂₁, y₂₂,… …, х_р, y_p1, y_p2….

б) затем в базис включаются векторы х_p+1, х_p+2, …, х_l, дополняющие базис М(А_) ∩ N(А_) до базиса ядра оператора А_ , если такие есть.

* Замечание: Процесс проводится для каждого значениядо тех пор, пока количество векторов, включенных в базис, не станет равным кратностиk собственного значения. Искомый базис:

х₁, y₁₁, y₁₂, …, х₂, y₂₁, y₂₂,… …, х_р, y_p1, y_p2…., х_p+1, х_p+2, …, х_l.

(Всего k векторов).